Afiliacja: Nauczyciel, Warszawa
Nasza saga, jak niejedna w matematyce, rozpoczyna się od stosunkowo nietrudnego zadania.
Zadanie. Na ścianach sześcianu napisano liczby 1, 2, 3, 4, 5, 6, każdą na dokładnie jednej ścianie. Następnie w każdy wierzchołek wpisano sumę liczb znajdujących się na ścianach sąsiadujących z tym wierzchołkiem. Czy jest możliwe, że w każdym wierzchołku otrzymano taką samą sumę?
Zadanie to ma co najmniej dwa istotnie różne rozwiązania.
Sposób 1 (globalny). Ponieważ każda ściana sąsiaduje z czterema wierzchołkami, więc suma liczb wpisanych w wierzchołki danego sześcianu jest równa \(4\cdot (1+2+3+4+5+6)=84.\) Nie jest ona podzielna przez 8 (a tyle jest wierzchołków), zatem nie jest możliwe, by liczby w wierzchołkach były równe.
Zastosowana w sposobie 1 technika nazywa się podwójnym zliczaniem. Skorzystamy z niej tu jeszcze kilka razy.
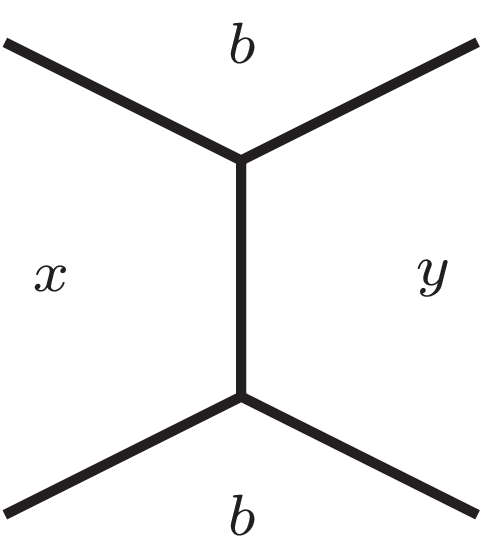
Sposób 2 (lokalny). Przypatrzmy się dowolnie wybranej krawędzi. Powiedzmy, że liczby na ścianach z nią sąsiadujących to \(x\) i \(y,\) a na ścianach, z którymi dzieli ona tylko wierzchołek, to \(a\) i \(b\) (rys. 1). Najbliższe otoczenie tej krawędzi symbolicznie przedstawia rysunek na marginesie. Sumy wpisane w wierzchołki będące jej końcami to \(x+y+a\) oraz \(x+y+b.\) Żeby więc były równe, potrzeba i wystarczy, aby \(a=b.\) To jest jednak niemożliwe, bo na ścianach sześcianu napisano parami różne liczby.
Rys. 1
Cała historia mogłaby się w tym miejscu zakończyć, gdyby nie to, że akurat w tej chwili postanowiła się zacząć. Po rozwiązaniu warto wszak podjąć refleksję nad pewnymi uogólnieniami obu metod, choćby na pozostałe wielościany foremne. Dla wygody wprowadzimy tu nowe pojęcie: dla wielościanu o \(S\) ścianach pięknym numerowaniem tych ścian nazwiemy takie napisanie na nich liczb \(1, 2, 3, \dots , S,\) że sumy liczb na ścianach sąsiadujących z każdym wierzchołkiem są równe.
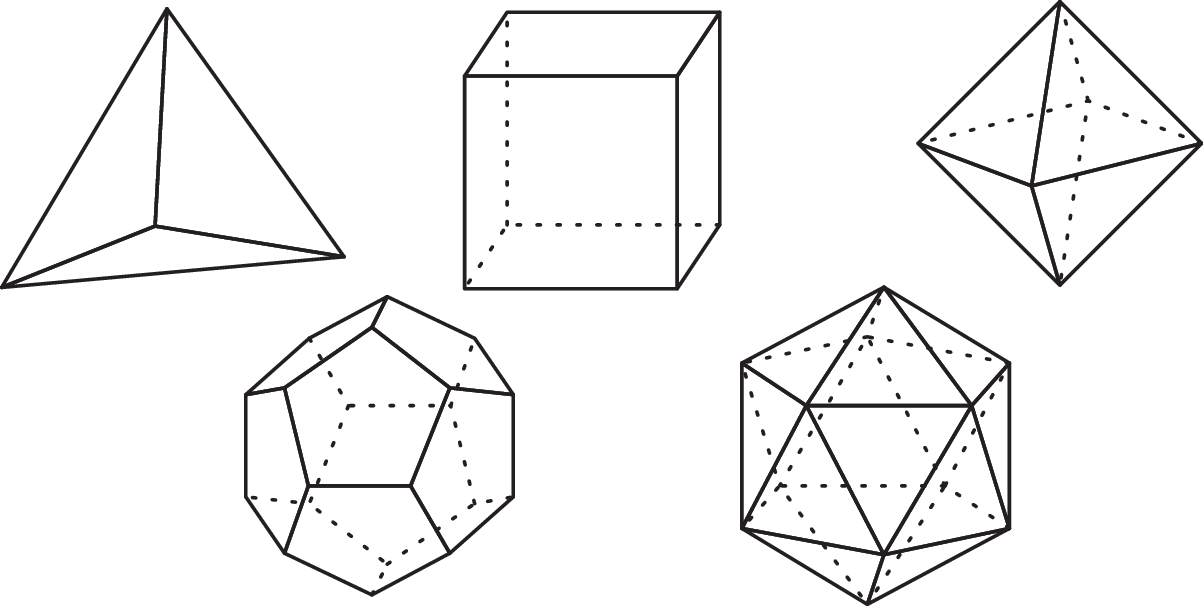
Ćwiczenie. Ściany których wielościanów foremnych (rys. 2) można pięknie ponumerować? W których przypadkach można to pytanie rozstrzygnąć argumentem globalnym, a w których lokalnym?
Rys. 2
Polowanie czas zacząć.
Dziękuję Antoniemu Deryło za postawienie tego brzemiennego w skutki pytania.
Celne pytanie postawił jeden z uczniów, którzy w czasie zajęć rozwiązali podane zadanie sposobem globalnym; mianowicie: czy gdyby otrzymana suma okazała się podzielna przez liczbę wierzchołków, to świadczyłoby to o wykonalności pięknego numerowania?
Formalnie odpowiedź jest oczywiście negatywna: to, że nie widzimy przeszkód, nie świadczy jeszcze o nieistnieniu takich przeszkód. Przekonał się o tym każdy, kto rozwiązywał choćby najprostsze zadania związane z metodą niezmienników. Wprawny retor rzekłby, że brak dowodu nie dowodzi braku. Z punktu widzenia dydaktyki warto jednak nie tylko się powymądrzać, ale też zilustrować swój argument stosownym przykładem. (Dzięki temu można zresztą powymądrzać się trochę dłużej). Poszukamy więc takiego wielościanu, którego ścian nie można pięknie ponumerować, przy czym faktu tego nie można wykazać argumentem globalnym. Chcielibyśmy jednak, aby wynikał on z argumentu lokalnego – wszak jakoś musimy dowieść niemożliwości owego pięknego numerowania.
O niezmiennikach pisaliśmy np. w \(\Delta^8_{19}\) oraz \(\Delta^7_{09}\).
Problem. Czy istnieje wielościan o \(S\) ścianach i \(W\) wierzchołkach spełniający poniższe warunki?
Zapis \(a|b\) oznacza, że liczba \(a\) jest dzielnikiem liczby \(b.\)
Istnieje liczba \(n\) taka, że każda ściana jest \(n\)-kątem;
\(W \,|\, n\cdot(1+2+3+\ldots +S)\);
w każdym wierzchołku spotykają się dokładnie \(3\) krawędzie.
Czytelnik Wnikliwy zauważy, że argument lokalny jest skuteczny w większej ogólności niż zaproponowana w punkcie iii). Myśl tę rozwija zadanie 3b.
Wielościan taki nazwiemy wielościanem uroczym.
Przyjrzyjmy się jeszcze powyższej definicji. Warunek i) gwarantuje, że argument globalny da się sformułować bez większych zmian; warunek ii) – że argument ten zawodzi; wreszcie dzięki iii) skuteczny jest argument lokalny, w szczególności dany wielościan istotnie nie dopuszcza pięknego numerowania ścian.
Niestety przykładu wielościanu uroczego podczas tej lekcji nie znaleziono, mimo że uczniowie, zachęceni obietnicą szóstek, czekoladek i uścisków dłoni, wypróbowali szereg rozmaitych pomysłów. Słowem – konieczne okazało się wezwanie artylerii.
Rysopis poszukiwanego.
Ponownie stosujemy zasadę podwójnego zliczania.
Poszukiwania wielościanu zaczniemy od zdobycia o nim dodatkowych informacji. Na przykład, skoro każda ściana wielościanu uroczego jest \(n\)-kątem (pierwszy warunek), a każda krawędź przylega do dwóch ścian, to \(nS=2K,\) gdzie \(K\) jest liczbą jego krawędzi. Podobnie z warunku iii) mamy, że \(2K=3W.\)
Powszechnie znany jest wzór na kolejne liczby trójkątne: \[1+2+3+\ldots +S=\frac{1}{2}S(S+1).\] Przekształcając równoważnie warunek ii), otrzymujemy kolejno: \(W \,|\, n\cdot\frac{1}{2}S(S+1),\) \(2W \,|\, nS(S+1),\) \(2W \,|\, 3W(S+1),\) \(2 \,|\, 3(S+1),\) \(2 \,|\, S+1.\) Zatem \(S\) jest liczbą nieparzystą. Wiemy zaś, że \(nS=2K,\) więc \(n\) musi być liczbą parzystą.
Podsumujmy nasze wnioski.
Stwierdzenie. Wielościan o \(S\) ścianach \(n\)-kątnych, \(K\) krawędziach i \(W\) wierzchołkach jest uroczy wtedy i tylko wtedy, gdy spełnia następujące warunki:
\(n\) jest liczbą parzystą;
\(S\) jest liczbą nieparzystą;
w każdym wierzchołku spotykają się dokładnie 3 krawędzie.
Ponadto zachodzi wówczas równość \(nS=2K=3W.\)
Stwierdzenie to samo w sobie stanowi dramatyczne uproszczenie wcześniejszej definicji wielościanu uroczego. Bezpośrednie poszukiwania nadal jednak nie przynoszą skutku. Może więc uda się w jakiś sposób wykluczyć istnienie wielościanów uroczych?
Detektyw Euler na pomoc.
Spróbujemy zastosować słynny wzór Eulera.
Więcej o wzorze Eulera można przeczytać np. w \(\Delta^3_{18}\).
Genus 0
Genus 2
Genus 5
Twierdzenie (wzór Eulera). Jeżeli w dowolnym wypukłym wielościanie oznaczymy przez \(S\) liczbę ścian, przez \(K\) – liczbę krawędzi, a \(W\) – liczbę wierzchołków, to spełniona jest zależność \(S+W=K+2.\)
Jest to już kolejna napotkana przez nas zależność wiążąca \(S, K, W.\) Podstawiwszy do niej spełnione w uroczym wielościanie równości \(K=\frac{1}{2}nS\) oraz \(W=\frac{1}{3}nS,\) wnioskujemy, że \(S+\frac{1}{3}nS=\frac{1}{2}nS+2.\) Stąd, po prostych przekształceniach, otrzymujemy równość \(S\cdot (6-n)=12.\)
Z otrzymanej równości wynika, że \(S\) jest dzielnikiem liczby 12. Oczywiście jako liczba ścian pewnego wielościanu \(S\geq 4.\) Jedynymi możliwymi wartościami \(S\) są więc 4, 6, 12 – same liczby parzyste. Nie może być zatem spełniony warunek ii\('\)), a w konsekwencji nie może istnieć wypukły wielościan uroczy.
Powyższe rozważania pokazują, że zależności podobne do wzoru Eulera mogą być bardzo użyteczne. Musimy jednak przenieść poszukiwania na inne obszary.
Koło ratunkowe.
Szczęśliwie się składa, że odpowiedniki wzoru Eulera istnieją także dla wielościanów niewypukłych. Kluczową charakterystyką wielościanu jest jego genus, który można rozumieć – przynajmniej na poziomie intuicyjnym – jako liczbę dziur owego wielościanu.
Twierdzenie (ogólny wzór Eulera). Dla wielościanu genusu \(g\) o \(S\) ścianach, \(K\) krawędziach i \(W\) wierzchołkach zachodzi związek \(S+W=K+2(1-g).\)
Podobnie jak ostatnio, dla uroczego wielościanu genusu \(g\) otrzymujemy stąd \[S(6-n)=12(1-g).\] Na swój sposób obiecująco wygląda więc przypadek \(g=1,\) w którym prawa strona tej równości jest równa \(0,\) zatem musi zachodzić \(n=6,\) za to \(S\) może być dowolną liczbą. Ta swoboda daje nadzieję na owocne poszukiwania.
Teraz, po zawężeniu obszaru poszukiwań do wielościanów ,,z jedną dziurą” i o sześciokątnych ścianach, możemy poprosić o pomoc wyszukiwarkę internetową. Istotnie, z jej pomocą udało się znaleźć nie jeden, ale dwa urocze wielościany! Oba zostały odkryte przez Lajosa Szilassiego i opisane w pracy z 1986 r.

Wielościany Szilassiego
Pierwszy wielościan ma znacznie prostszą strukturę – to zwykły sześcian z chytrze wydrążoną dziurą. Jednak to ten drugi został zapamiętany jako wielościan Szilassiego. Ma on szereg innych interesujących własności. Na przykład każda jego ściana sąsiaduje z każdą z pozostałych, co jest najgorszą możliwą sytuacją dla pięknego numerowania ścian. Wśród wielościanów jest to zjawisko niesamowicie rzadkie.
Przedstawiony rysunek prawdopodobnie nie jest przekonującym dowodem istnienia wielościanu Szilassiego. Autor zachęca do wykonania modelu – gotowe siatki są dostępne w Internecie. Warto też zajrzeć do wspomnianej pracy, w której przedstawione są szczegółowe obliczenia.
Zadania
1. Rozwiąż zadanie o pięknym numerowaniu ścian sześcianu sposobem innym niż dwa przedstawione na początku artykułu. Dla jakich innych wielościanów można go zastosować?
Oczywiście nie jest możliwe przewidzenie wszystkich sposobów rozwiązania, ale jeden z nich jest następujący. Wybierzmy dowolnie jedną parę przeciwległych wierzchołków naszego sześcianu. Ponieważ każda ściana sześcianu sąsiaduje z dokładnie jednym z nich, więc suma liczb w tych wierzchołkach wynosi \(1+2+3+4+5+6=21.\) Jest to liczba nieparzysta, więc liczby wpisane w tych wierzchołkach nie mogą być równe.
Ten sposób rozwiązania jest skuteczny dokładnie wtedy, gdy spośród wierzchołków danego wielościanu można wybrać \(w\) wierzchołków tak, że każda ściana sąsiaduje z dokładnie jednym z nich, a ponadto \(w \nmid 1+2+3+\dots +S=\frac{1}{2}S(S+1).\) Przykładem takiej bryły jest każda podwójna piramida o liczbie ścian niepodzielnej przez 4 (wybieramy dwa wierzchołki tworzących ją ostrosłupów) lub przedstawiony poniżej sześćdziesięciościan (wybieramy wierzchołki, w których spotyka się po 5 krawędzi). Czytelnikowi pozostawiamy sprawdzenie, że podwójna piramida o 14 ścianach jest przy tym odporna na oba argumenty podane na początku artykułu, podczas gdy pozostałe przypadki daje się rozwiązać sposobem globalnym.
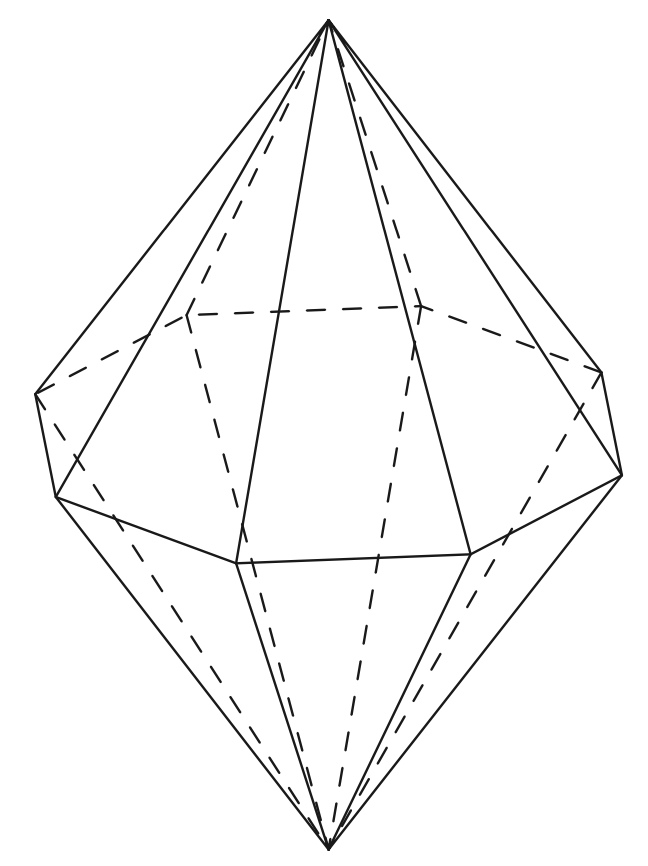

podwójna piramida ośmiokątna / pentagonal hexecontahedron
2. Jak zmodyfikować treść zadania o pięknym numerowaniu ścian sześcianu (inaczej niż zmieniając wielościan), tak aby nadal można je było rozwiązać sposobem lokalnym, ale nie globalnym?
Można choćby zmienić zestaw wpisywanych liczb tak, aby były nadal parami różne, ale żeby ich suma była już podzielna przez 8, np. 1, 2, 3, 4, 5, 9.
3. Wykaż, że nie jest możliwe piękne ponumerowanie ścian: a. żadnego graniastosłupa; b. żadnego ostrosłupa.
a. Wynika to natychmiast z argumentu lokalnego, z wykorzystaniem dowolnej krawędzi. Interesujące, że argument globalny nie daje się nawet sformułować, bo podstawy i ściany boczne mają różne liczby wierzchołków (jedynym wyjątkiem jest, rzecz jasna, graniastosłup czworokątny).
b. Zauważmy, że i tutaj argument lokalny jest skuteczny, ale trzeba zastosować go do krawędzi podstawy. Podobnie jak ostatnio, argument globalny nie daje się sformułować (wyjątkiem jest czworościan).
4. Wykaż, że każdy wielościan wypukły ma ścianę, która jest wielokątem o co najwyżej pięciu bokach.
W każdym wierzchołku wielościanu spotykać się muszą co najmniej 3 krawędzie, stąd \(3W\leq 2K.\) Zatem \(W\leq \frac{2}{3}K.\) Załóżmy, że każda ściana jest wielokątem o co najmniej 6 bokach; wówczas \(6S\leq 2K,\) zatem \(S\leq \frac{1}{3}K.\) Łącząc te wnioski z wzorem Eulera, otrzymujemy \(2=S-K+W\leq \frac{1}{3}K-K+\frac{2}{3}K=0.\) Ta sprzeczność dowodzi tezy zadania.
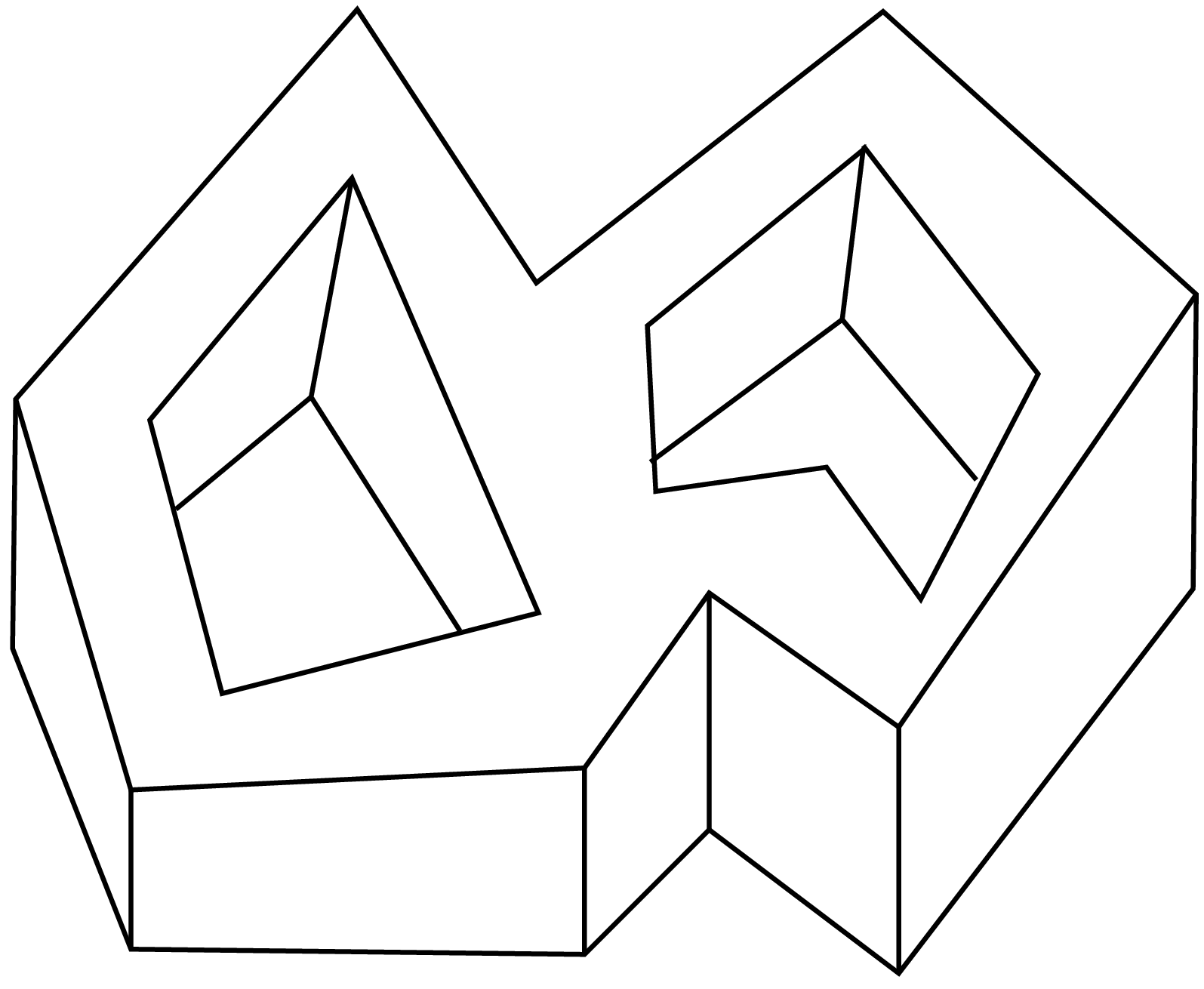
5. Znajdź wielościan, który ma dokładnie 16 ścian, 32 krawędzie i 16 wierzchołków.
Taki wielościan przedstawia poniższy rysunek.
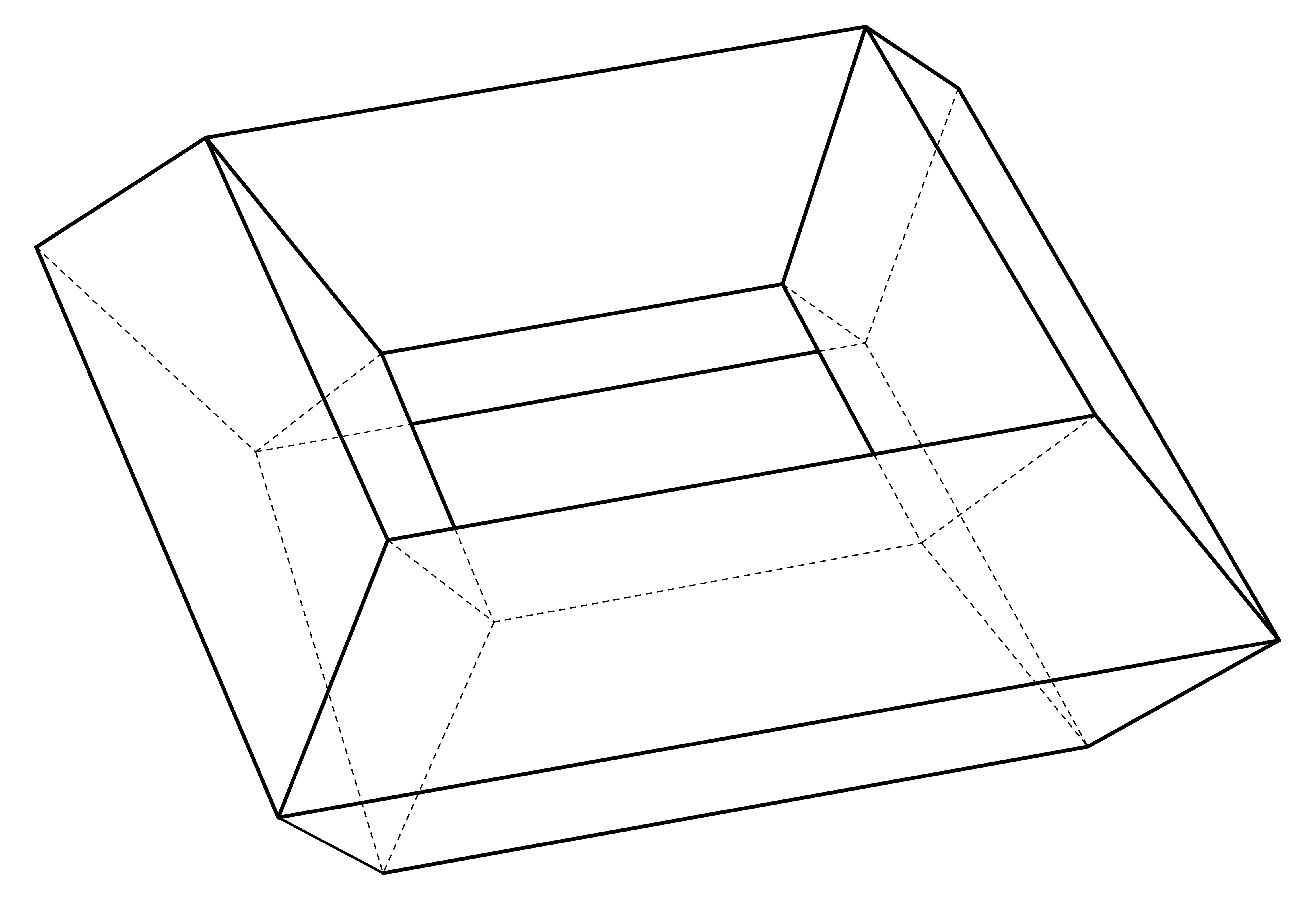
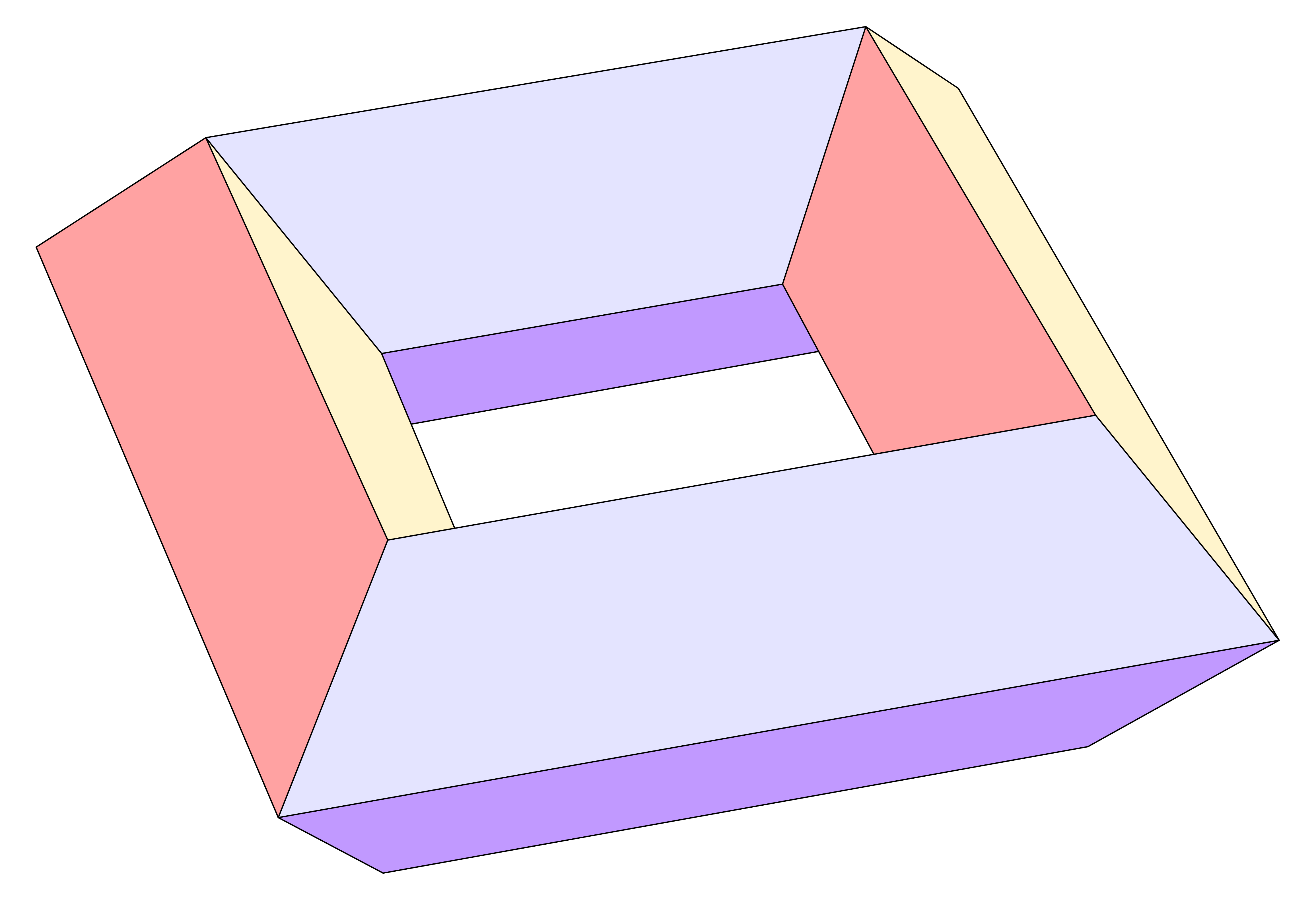
Uczniowie sporadycznie twierdzą, jakoby z wzoru Eulera wynikało nieistnienie takiego wielościanu. W rzeczywistości wynika zeń tylko, że musi to być wielościan genusu 1 – w szczególności nie może być on wypukły.
6. Wykaż, że nie istnieje uroczy wielościan genusu 2 ani 3.
W sekcji ,,Koło ratunkowe” pokazaliśmy, że dla uroczego wielościanu genusu \(g\) zachodzi równość \(S(6-n)=12(1-g).\) Gdy \(g=2, 3,\) równość ta przybiera postać \(S(6-n)=-12\) lub \(S(6-n)=-24,\) zatem \(S\) jest dzielnikiem liczby 12 lub 24, odpowiednio. To jest jednak niemożliwe. Istotnie, zgodnie z warunkiem ii’), \(S\) musi być liczbą nieparzystą. Ponadto jako liczba ścian wielościanu musi wynosić co najmniej 4. Tymczasem największym nieparzystym dzielnikiem liczb odpowiednio 12 i 24 jest liczba 3.
7. Wykaż, że nie istnieje uroczy wielościan genusu \(2^k+1,\) gdzie \(k\) jest dowolną liczbą naturalną.
Uogólnimy rozumowanie podane w rozwiązaniu poprzedniego zadania. Dla \(g=2^k+1\) mamy \(S(6-n)=12\cdot 2^k = 3\cdot 2^{k+2}.\) Ponownie więc \(S,\) jako nieparzysty dzielnik prawej strony, równe jest co najwyżej 3. Jest to jednak niemożliwe, bo każdy wielościan ma co najmniej 4 ściany.
8. Ile ścian może mieć uroczy wielościan genusu 4?
W tym przypadku otrzymujemy \(S(6-n)=12\cdot (1-4)=-36.\) Nieparzyste dzielniki liczby 36 to 1, 3, 9. Skoro zaś \(S\geq 4,\) więc \(S=9.\) Konsekwentnie \(6-n=-4,\) czyli \(n=10.\) Wobec czego taki wielościan musi mieć 9 ścian dziesięciokątnych.
Nie jest wcale jasne, czy taki wielościan istnieje. Jak dotąd braliśmy pod uwagę jedynie jego własności o charakterze kombinatorycznym. Pozostaje więc niewykluczone, że taka bryła nie da się zrealizować geometrycznie. Problem jest otwarty.
9. Wykaż, że każdy wielościan uroczy ma co najmniej 7 ścian.