Jej wysokość krzywa eliptyczna

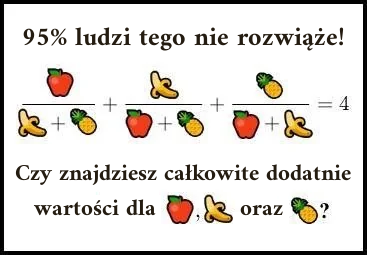
Internet jest pełen krzykliwych haseł mających przyciągnąć uwagę użytkownika. Lekarze nie chcą, byś poznał cudowne własności tego wodorostu!, Ta prosta sztuczka pozwoli ci zarabiać miliony bez wychodzenia z łazienki!, Mężczyzna próbował podzielić przez zero, zobaczcie, co się stało dalej! – to tylko wymyślone na poczekaniu przykłady, wcale nieodległe od pierwowzorów. Wśród tych fraz szczególne miejsce zajmują te rachunkowo-logiczne, rozpoczynające się od $K$% ludzi tego nie rozwiąże!, gdzie $K\in [90,100).$ Przyjrzyjmy się jednemu z takich clickbaitów, przedstawionemu na marginesie – sprawdźmy, czy jako osoby o ścisłych inklinacjach znajdujemy się w chlubnych $(100-K)\mathrm{\%}$ populacji.

Dla Czytelników Delty nie ma niestety żadnych jabłek, bananów i ananasów – są za to całkowite dodatnie liczby $x,y,z,$ które mają spełniać równanie $$\begin{array}{}\text{(1)}& \frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=4.\end{array}$$ Czy takie istnieją? Szukając jakichkolwiek rozwiązań, możemy zastanowić się najpierw, czy nie istnieją takie, które spełniają pewne upraszczające założenia. Gdy $x=y=z,$ nasze równanie sprowadza się do postaci $\frac{3}{2}=4,$ zatem wtedy rozwiązań nie ma. Z kolei gdy przyjmiemy tylko $x=y,$ to $\text{(1)}$ sprowadza się do równania kwadratowego ze względu na $z,$ którego rozwiązanie to $z=\frac{1}{2}(7\pm \sqrt{65})x.$ Oznacza to, że wtedy również brak rozwiązań całkowitych (liczby $x$ i $z$ nie mogą być jednocześnie całkowite). A czy któraś z tych liczb może być równa 0? Niestety nie – gdyby na przykład zachodziła równość $x=0,$ to $\text{(1)}$ ponownie stałoby się równaniem kwadratowym z rozwiązaniem $z=(\pm 2+\sqrt{3})y,$ co również jest niemożliwe dla liczb całkowitych $y,z.$ Podstawowe próby uproszczenia równania dodatkowymi założeniami spełzły zatem na niczym.

Bywa, że umysłowa ekwilibrystyka musi ustąpić brutalnej sile. Nietrudno napiszemy prosty skrypt, który przejrzy wszystkie trójki liczb całkowitych dodatnich od 1 do, powiedzmy, 100 i sprawdzi, czy spełniają one równość $\text{(1)}$. Okazuje się, że taki program nie znajdzie żadnego rozwiązania w tym zakresie. Jeśli z ciekawości pozwolimy mu przeglądać liczby ujemne (o module nie większym niż 100), to z dokładnością do kolejności oraz skalowania dostaniemy dwa rozwiązania: $(-1,4,11),$ $(-5,9,11).$ Wspomniane skalowanie wiąże się z obserwacją, że jeśli $(x,y,z)$ jest rozwiązaniem $\text{(1)}$, to jest nim również $(ax,ay,az)$ dla $a\ne 0$ – w naszych poszukiwaniach możemy zatem ograniczyć się do trójek, których największy wspólny dzielnik jest równy 1.

Problem z naszym podejściem polega na tym, że złożoność takiego prymitywnego programu (tzn. liczba trójek liczb do sprawdzenia) zwiększa się sześciennie wraz z wielkością zakresu. Przy odrobinie cierpliwości moglibyśmy zatem w ten sposób poszukać rozwiązań w przedziale od 1 do 1000, ale już przedział $[1,{10}^4]$ pozostaje raczej poza możliwościami zwykłego laptopa. Przy odrobinie pomysłowości możemy jednak uzyskać z grubsza kwadratowy koszt przeszukiwań i w ten sposób przekonać się, że nie istnieją rozwiązania w tym przedziale. Cóż, jeśli tak proste równanie jak $\text{(1)}$ nie ma rozwiązań całkowitych w tak szerokim zakresie, to na pewno nie ma ich w ogóle – a cała zagadka jest pomyłką albo złośliwym żartem.

Okazuje się, że owszem mamy do czynienia ze złośliwym żartem, ale bardziej przewrotnym niżby mogło się nam wydawać – otóż wyjściowe równanie istotnie ma rozwiązania w liczbach całkowitych dodatnich, przy czym najmniejsze z nich jest postaci: $$\begin{array}{rl}x& =\text{ 4373612677928697257861252602371390152816537558161613618621437993378423467772036},\\ y& =\text{ 154476802108746166441951315019919837485664325669565431700026634898253202035277999},\\ z& =\text{ 36875131794129999827197811565225474825492979968971970996283137471637224634055579},\end{array}$$ gdzie $x$ ma aż 79 cyfr! Jak można odnaleźć tak ogromne rozwiązania i skąd wiadomo, że nie ma mniejszych? Temu zagadnieniu poświęcona będzie dalsza część artykułu.

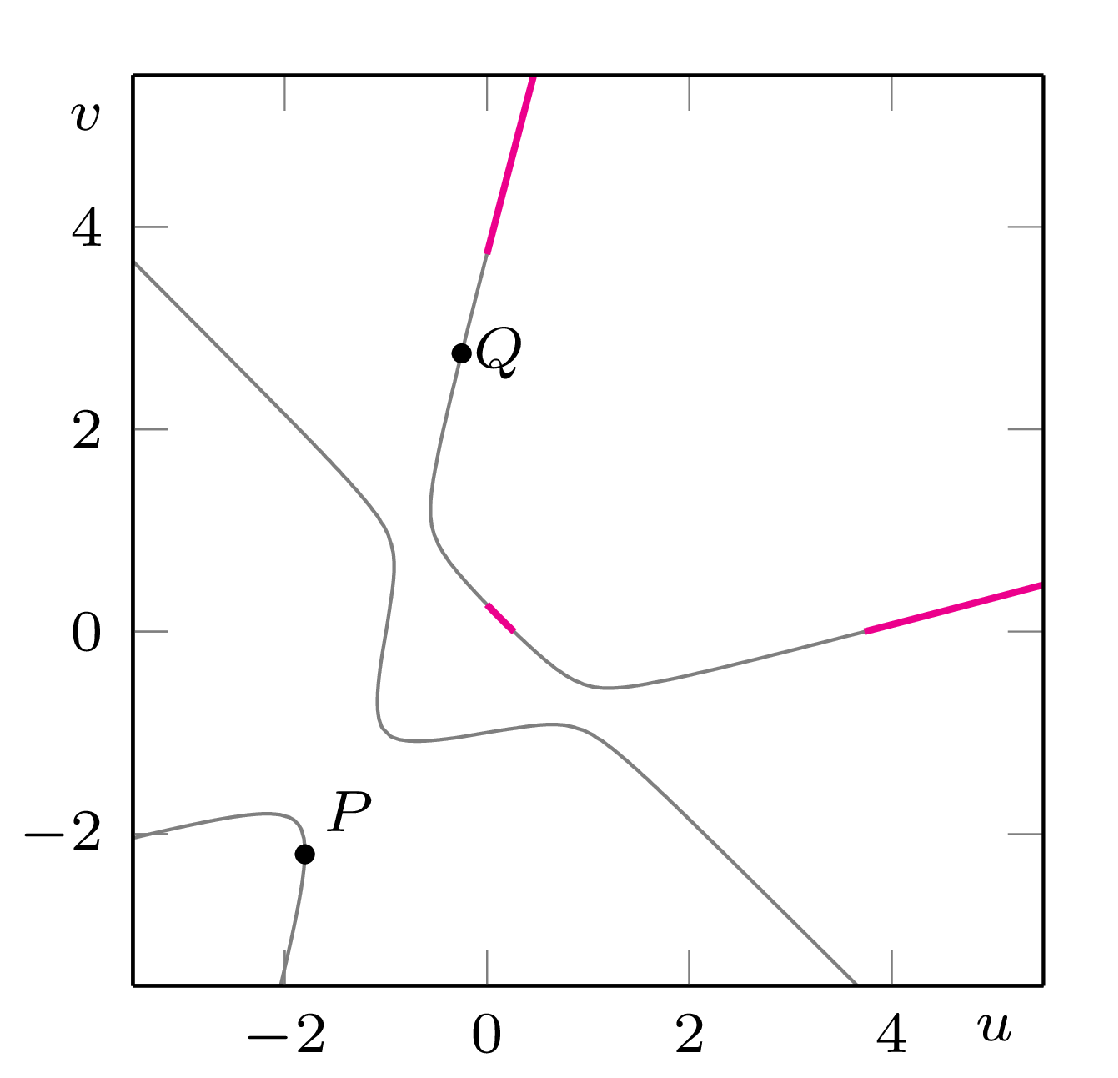
Trójki różnych od zera liczb całkowitych $(x,y,z),$ których największy wspólny dzielnik jest równy 1, można jednoznacznie zakodować jako pary $(u,v),$ gdzie $u=x/z$ i $v=y/z.$ Po takim zabiegu równanie $\text{(1)}$ staje się równaniem dwóch zmiennych następującej postaci: $$\begin{array}{}\text{(2)}& (u+v{)}^3-6uv(u+v)-3(u+v{)}^2-3(u+v)+uv+1=0.\end{array}$$ Jest to równanie pewnej krzywej $C$ stopnia $3,$ przedstawionej na rysunku 1. Zaznaczono na niej punkty $P=(-9/5,-11/5)$ i $Q=(-1/4,11/4)$ odpowiadające rozwiązaniom $(-9,-11,5)$ i $(-1,11,4)$ równania $\text{(1)}$. Kolorem oznaczono te fragmenty krzywej $C,$ które leżą w I ćwiartce. Jeśli znajdziemy na tym kolorowym fragmencie punkt o współrzędnych wymiernych – odtąd punkty takie będziemy nazywać wymiernymi – będzie on odpowiadał dodatniemu rozwiązaniu $\text{(1)}$. Tylko jak takich punktów szukać? Z pomocą przyjdzie nam… geometria! Okazuje się bowiem, że

Dowód tego faktu wynika z zastosowania wzorów Vièta po wstawieniu do $\text{(2)}$ liniowej zależności $v=\alpha u+\beta .$ Szczegóły uzasadnienia zamieszczone są na końcu artykułu – jest tam również przedstawiony jawny wzór pozwalający wyznaczyć współrzędne punktu $R$ w zależności od współrzędnych $P$ i $Q.$

Dla przykładu, jeśli na rysunku 1 poprowadzimy prostą przez punkty $P$ i $Q,$ to przetnie ona krzywą $C$ w jeszcze jednym punkcie $R$ o współrzędnych $(-9071/9841,5951/9841).$ Daje nam to kolejne całkowite rozwiązanie $\text{(1)}$ ($x=-9071,$ $y=5951$ i $z=9841$), które jednak wciąż nie jest dodatnie.

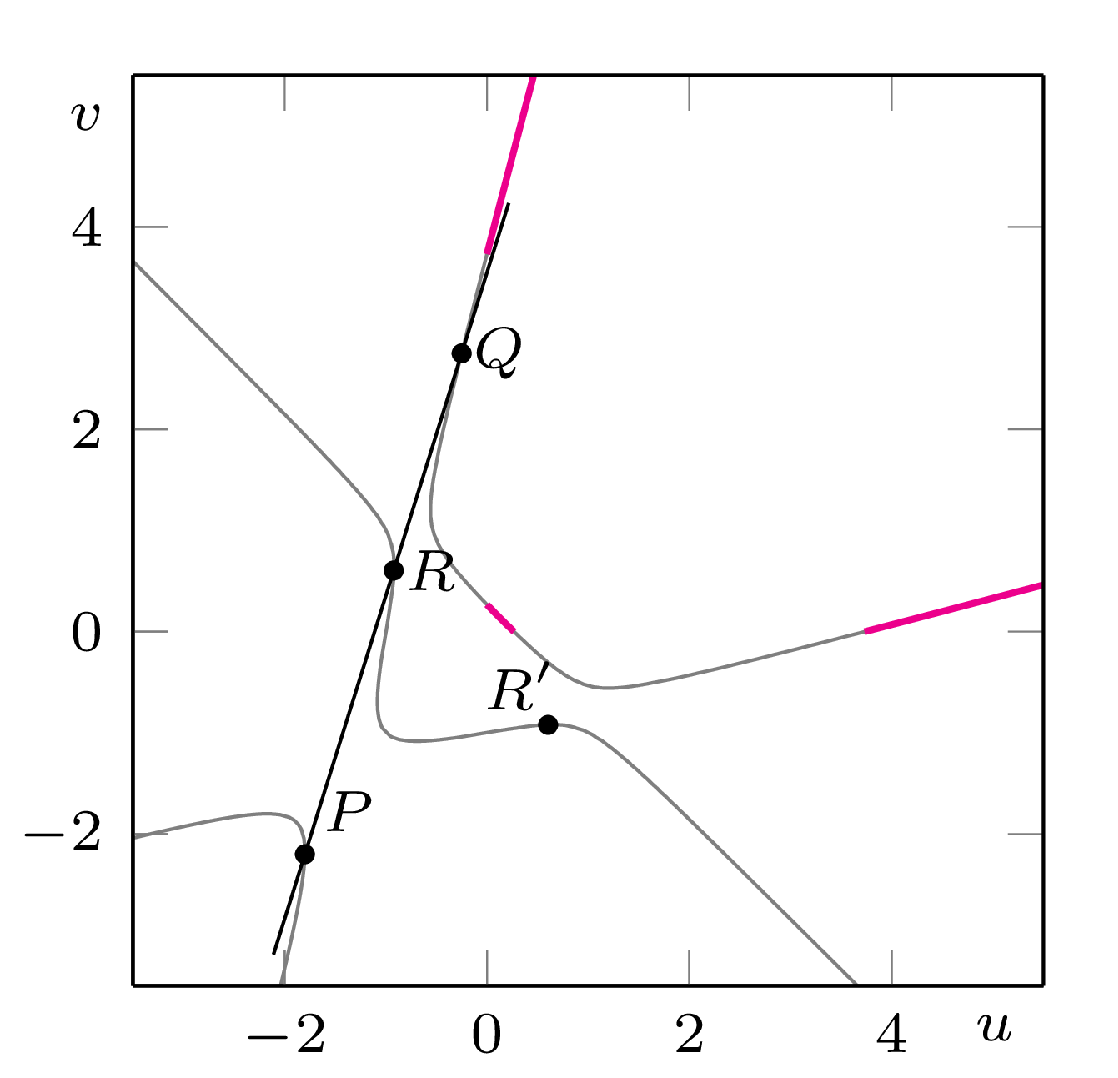
Na pierwszy rzut oka na tym kończy się nasza przygoda z generowaniem nowych punktów – każda prosta ma co najwyżej trzy punkty przecięcia z krzywą $C.$ Z pomocą przychodzi nam operacja wręcz trywialna – zamiana współrzędnych miejscami! Jeśli $(u,v)$ spełnia równanie $\text{(2)},$ to $(v,u)$ również je spełnia. Jeśli zatem punkt $R$ leży na $C,$ to symetryczny do niego względem prostej $u=v$ punkt $R^{\prime }$ również – i, rzecz jasna, on też ma współrzędne wymierne (rys. 2). Te dwie operacje: branie trzeciego punktu przecięcia z $C$ oraz zamiana współrzędnych miejscami, pozwalają nam wygenerować dowolnie wiele punktów wymiernych. Pozostaje nam mieć nadzieję, że w końcu trafimy w ten sposób na punkt o współczynnikach dodatnich.

Przeprowadźmy poszukiwania w sposób systematyczny. Dla ułatwienia notacji wyżej przedstawioną konstrukcję punktu $R^{\prime }$ z punktów $P$ i $Q$ oznaczmy jako $m(P,Q).$ Z powodów, które staną się zrozumiałe później, wprowadźmy leżący na krzywej $C$ punkt $T=(-1,1)$ i przyjmijmy oznaczenia $P_1=m(T,P)$ oraz $P_{n+1}=m(P_n,P).$ Zgodnie z wcześniejszymi obserwacjami wszystkie punkty $P_n$ leżą na krzywej $C.$ Możemy kolejno obliczać ich współrzędne (raczej przy pomocy komputera), aż w końcu… Udało się! Punkt $P_9$ ma obie współrzędne dodatnie, a więc wyznacza nam pewne dodatnie rozwiązanie naszego oryginalnego problemu $\text{(1)}$. Jest to dokładnie to gigantyczne rozwiązanie, które przedstawiliśmy wcześniej – jak widać, potrzeba sporo jabłek…

Zaskakujące jest to, że każda z liczb $x,y,z$ tego rozwiązania ma około 80 cyfr. Z pewnością takiego rozwiązania nie znaleźlibyśmy ręcznie. Pozostają więc pytania:

1. Czy można znaleźć mniejsze (w sensie maksimum) rozwiązanie?

2. Czy wykorzystana operacja $m(P,Q)$ ma jakiś głębszy sens?

3. Czy i kiedy znajdziemy ,,małe” rozwiązanie początkowe w ogólnej sytuacji?

W dalszej części spróbujemy – na tyle, na ile jest to możliwe – uzasadnić negatywną odpowiedź na pytanie (A). Wykorzystamy do tego strukturę grupy związaną z odpowiedzią na pytanie (B) i zakończymy bardzo trudnymi pytaniami matematycznymi, które wiążą się z odpowiedzią (wciąż niepełną!) na pytanie (C).

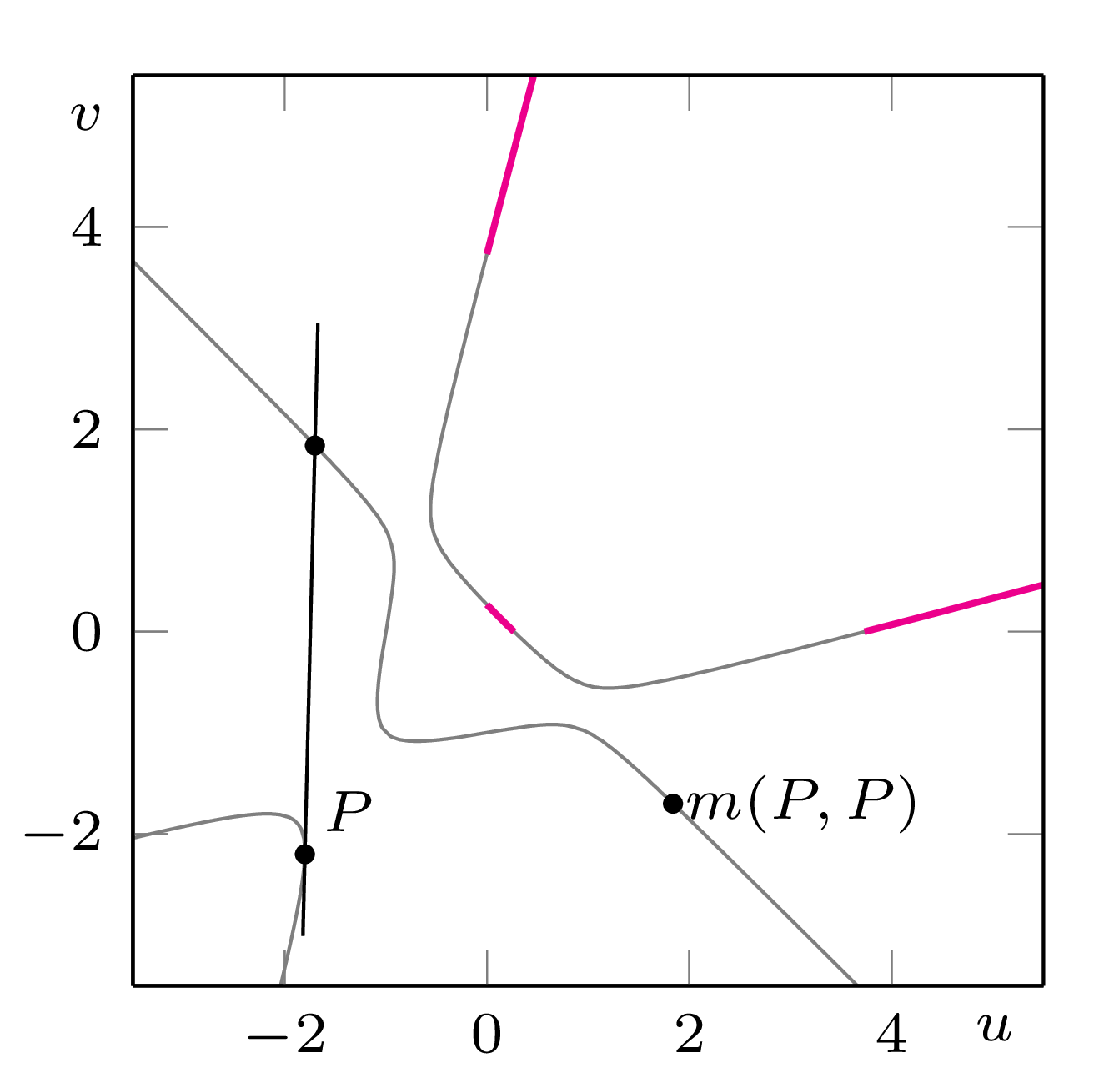
Przyjrzyjmy się uważniej operacji $m(P,Q).$ Wiemy już, że nie wyprowadza ona poza zbiór punktów $C$ o wymiernych współrzędnych. Jest też w oczywisty sposób symetryczna, tzn. $m(P,Q)=m(Q,P).$ Okazuje się, że ma jeszcze inną przydatną, choć niełatwą w uzasadnieniu własność: dla dowolnych punktów $P,Q,R$ na $C$ zachodzi: $$m(m(P,Q),R)=m(P,m(Q,R)).$$ W fachowej terminologii oznacza to, że jest to operacja łączna, i dzięki wcześniejszej symetrii możemy o niej myśleć jak o zwykłym działaniu, takim jak na przykład dodawanie. Przeszkadzać może odrobinę, że operacja $m(P,Q)$ zdefiniowana była dla różnych punktów $P$ i $Q$ (by można było poprowadzić przez nie prostą). Chcąc zdefiniować $m(P,P),$ możemy jednak pomyśleć o granicy $m(P,R_n),$ gdzie $R_n$ jest ciągiem punktów na $C$ zbiegających do $P.$ Wówczas w pierwszym kroku operacji $m$ zamiast prostej przechodzącej przez dwa punkty bierzemy styczną do $C$ w punkcie $P$ (rys. 3). Inna trudność pojawia się, gdy chcemy wykonać operację $m(P,Q)$ na dwóch punktach symetrycznych względem prostej $y=x.$ Z dowodu stwierdzenia ($\mathrm{♡}$), zamieszczonego na końcu artykułu, wynika, że nie istnieje wtedy trzeci punkt przecięcia prostej $PQ$ z krzywą $C.$ Jeśli powiemy, że wówczas wynikiem zawsze ma być pewien abstrakcyjny punkt $\mathcal{O},$ o który wzbogacamy krzywą $C$ (można o nim myśleć jako o punkcie definiującym kierunek $(-1,1)$), to już nic nie stoi na przeszkodzie, aby myśleć o $m$ jako o porządnym ,,dodawaniu” punktów na krzywej $C$ – od tej pory przyjmujemy zatem oznaczenie $P+Q:=m(P,Q).$ Pozwala nam to też mnożyć punkty przez liczby całkowite: dla $n\in \mathbb{N}$ punkt $nP$ to efekt $n$-krotnego dodania do siebie punktu $P,$ zaś $-nP$ to odbicie symetryczne $nP$ względem prostej $u=v.$ Zdefiniowane w ten sposób działanie dodawania punktów krzywej trzeciego stopnia daje w rezultacie strukturę grupy nazywaną krzywą eliptyczną.

Wspominaliśmy już, że rozwiązania równania $\text{(1)}$ można ograniczyć do trójek liczb $(x,y,z),$ których największy wspólny dzielnik jest równy 1. Warto tu zaznaczyć, że wówczas liczby $x,y,z$ są parami względnie pierwsze. Istotnie, równanie $\text{(1)}$ można sprowadzić do postaci $$x^3+y^3+z^3-3x^{2}y-3x^{2}z-3x{y}^2-3x{z}^2-3y^{2}z-3y{z}^2-5xyz=0,$$ z której wynika, że każdy wspólny dzielnik pierwszy dowolnych dwóch spośród liczb $x,y,z$ dzieli też trzecią z tych liczb, więc również największy wspólny dzielnik całej trójki – czyli 1. Ta obserwacja oznacza również, że jeśli współrzędne dowolnego wymiernego punktu $(u,v)$ krzywej $C$ przedstawimy w postaci nieskracalnej, to będzie to postać $(x/z,y/z),$ tłumacząca się bezpośrednio na rozwiązanie $(x,y,z)$ równania $\text{(1)}$.

Wprowadzimy teraz pewną ciekawą funkcję, nazywaną wysokością. Dla wymiernego punktu $P=(u,v)$ definiujemy $h(P)={\log }_{10}(max\{|a|,|b|\}),$ gdzie $\frac{a}{b}$ jest nieskracalną postacią $u+v.$ Na przykład dla $P=(-9/5,-11/5)$ otrzymujemy zatem $h(P)={\log }_{10}4.$ Zauważmy, że jeśli $P=(x/z,y/z)$ ma współrzędne dodatnie, to $h(P)\le {\log }_{10}(max\{x+y,z\}),$ zatem $h(P)\le {\log }_{10}(2max\{x,y,z\}).$ Z dokładnością do ${\log }_{10}(2)\approx 0,3$ funkcja $h$ ogranicza więc z dołu liczbę cyfr największej spośród liczb $x,y,z$ – może być zatem użyteczna dla badania fenomenu ogromnego rozwiązania równania $\text{(1)}$.

Zachodzi następujące ciekawe twierdzenie: dla każdego punktu $P$ wymiernego na krzywej $C$ istnieje granica ciągu $(\frac{h(2^{n}P)}{4^n}).$ Oznaczamy tę granicę przez $\hat{h}(P)$ i nazywamy wysokością kanoniczną. Jak zostało udowodnione przez André Nérona i Johna Tate’a (na dwa różne sposoby!):

1. $\hat{h}(nP)=n^2\hat{h}(P)$ (tzn. $\hat{h}(P)$ jest formą kwadratową);

2. $\hat{h}(P+Q)+\hat{h}(P-Q)=2\hat{h}(P)+2\hat{h}(Q)$ dla dowolnych punktów $P,Q$ (tzw. prawo równoległoboku);

3. istnieje stała $\kappa >0$ taka, że $|h(P)-\hat{h}(P)|<\kappa$ niezależnie od wyboru punktu $P.$

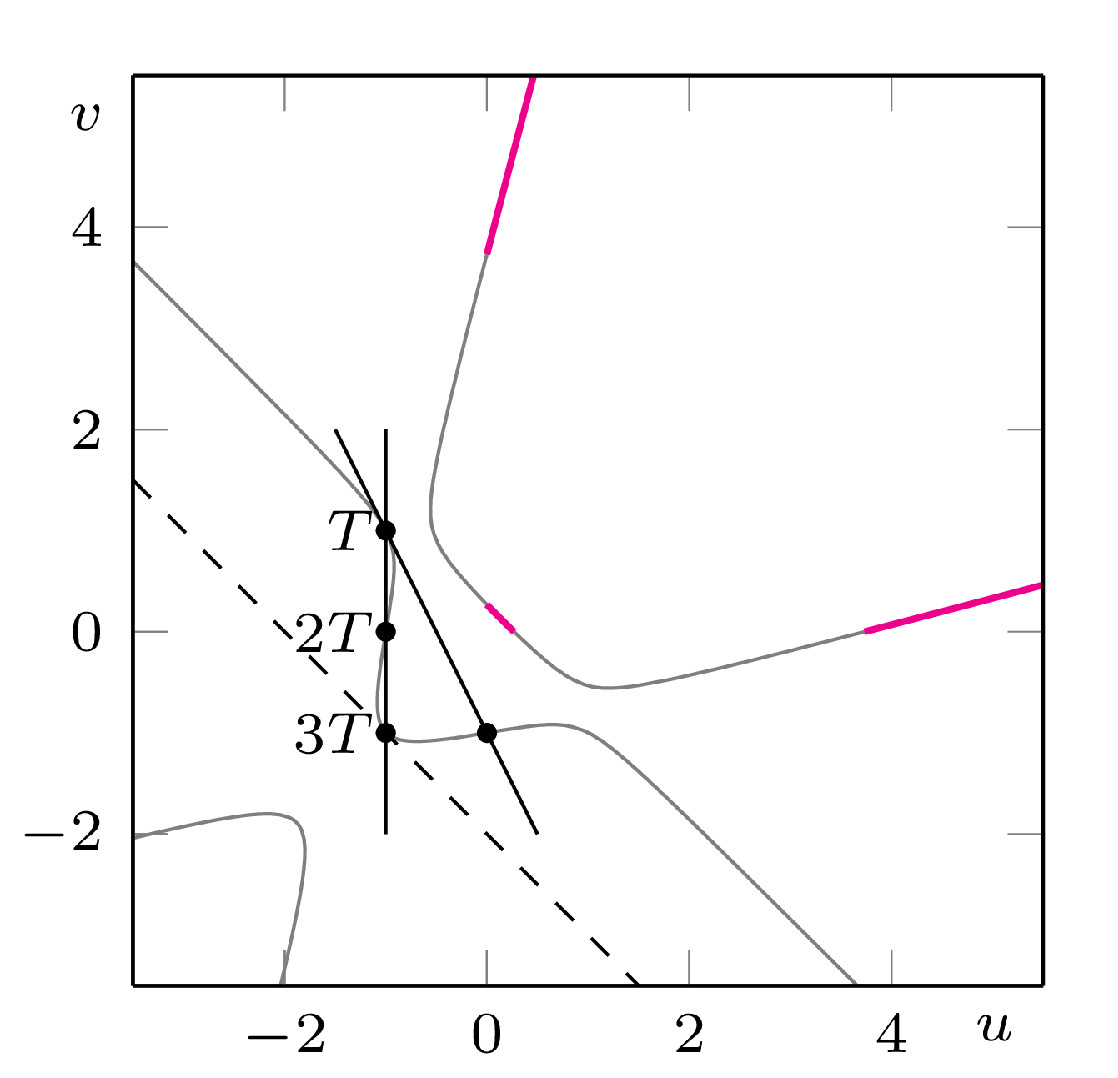
Uzbrojeni w takie nowe narzędzia możemy teraz bez trudu wyjaśnić, dlaczego skonstruowany wcześniej punkt $P_9=9P+T$ tłumaczył się na tak monstrualnej wielkości rozwiązanie równania $\text{(1)}$. Można sprawdzić, że $3T=(-1,-1)$ (rys. 4) oraz $2(-1,-1)=\mathcal{O},$ zatem $6T=\mathcal{O}$ i dlatego zgodnie z własnością (a) zachodzi $\hat{h}(T)=\frac{1}{36}\hat{h}(\mathcal{O})=0.$ Z prawa równoległoboku wynika zatem, że dla dowolnego punktu $S$ oraz $i\in \mathbb{N}$ zachodzi: $$\hat{h}(S+(i+1)T)+\hat{h}(S+(i-1)T)=2\hat{h}(S+iT).$$ Oznacza to, że ciąg $(\hat{h}(S+iT){)}_i$ jest ciągiem arytmetycznym. Z drugiej strony $S+6T=S,$ zatem jest to jednocześnie ciąg okresowy, więc musi być ciągiem stałym. Wstawiając $S=9P,$ dostajemy $\hat{h}(9P+T)=\hat{h}(9P),$ i ponownie własność (a) implikuje $\hat{h}(9P)=81\hat{h}(P).$ Zgodnie z (c) możemy zatem zapisać $h(9P+T)\approx 81h(P)$ (Błąd przybliżenia $\kappa$ nie zależy od wyboru punktu, a jedynie od samego równania krzywej $C$!) Można to zinterpretować w taki sposób, że liczba cyfr największej liczby w nieskracalnym zapisie $9P+T$ wzrosła około 81 razy w stosunku do analogicznej liczby cyfr dla punktu $P.$ Zauważmy, że ta jakościowa analiza bardzo dobrze odpowiada uzyskanym przez nas dokładnym wynikom.

Ale skąd wiemy, że punkt $9P+T$ jest najmniejszy w sensie liczby cyfr, który dopuszcza dodatnie rozwiązania? Odpowiedź kryje się w twierdzeniu udowodnionym przez Luisa Mordella w 1922 roku. Aby sformułować je w pełnym brzmieniu, zdefiniujmy rząd punktu $S$ jako najmniejszą liczbę naturalną $n$ taką, że $nS=\mathcal{O}$ (jeśli takiej liczby nie ma, przyjmujemy rząd równy $\mathrm{\infty }$). Twierdzenie Mordella głosi, że na krzywej eliptycznej istnieje skończony zbiór punktów $T_1,\dots T_k$ (skończonego rzędu) oraz $P_1,\dots ,P_r$ (rzędu nieskończonego) taki, że każdy punkt wymierny zapisuje się jako suma $\sum _i{a}_i{P}_i+\sum _k{b}_k{T}_k,$ gdzie $a_i,b_k$ są liczbami całkowitymi. Dla każdego punktu liczby te są wyznaczone jednoznacznie. Liczbę $r$ nazywamy wówczas rangą krzywej eliptycznej $C,$ a punkty $P_i$ i $T_k$ jej generatorami.

W przypadku naszej krzywej $C$ dodatkowe rachunki algebraiczne (zdecydowanie wykraczające poza ramy tego artykułu) pozwalają udowodnić, że każdy punkt wymierny jest postaci $kP+lT.$ Zatem każdy punkt wymierny na naszej krzywej ma wysokość kanoniczną równą $\hat{h}(kP+lT)=k^2\hat{h}(P),$ odpowiadającą w przybliżeniu ,,zwykłej” wysokości. Pozostaje więc tylko upewnić się, że wszystkie punkty $kP+lT$ dla $-9<k<9$ oraz $0\le l\le 5$ nie mają obu współrzędnych dodatnich (ograniczenie na $l$ wynika z faktu, że $6T=\mathcal{O}$).

W ten sposób nasze rozważania prowadzą do jednego z najsłynniejszych problemów w matematyce, czyli hipotezy Bircha–Swinnertona–Dyera. Postuluje ona istnienie efektywnego algorytmu wyznaczającego generatory punktów na krzywej eliptycznej. Dodatkowo hipoteza ta – jeśli jest prawdziwa – pozwala opisać związek między wysokościami punktów generujących i arytmetyką samej krzywej eliptycznej. Przy założeniu, że ranga krzywej eliptycznej wynosi $0$ lub $1,$ hipoteza BSD została udowodniona dla nieskończenie wielu krzywych eliptycznych.

Na koniec polecamy Czytelnikom interesujące eksperymenty. Możemy poszukiwać ,,prostego” (minimalnego w sensie wysokości) rozwiązania równania $\text{(1)}$, w którym liczba $4$ została zastąpiona inna liczbą wymierną. Są częściowe wyniki na ten temat, więcej informacji można znaleźć w artykule [$\ast$]. Okazuje się, że generatory krzywej eliptycznej mogą być naprawdę ogromne!

Uzasadnienie stwierdzenia ($\mathrm{♡}$).

Zastanówmy się, ile punktów wspólnych może mieć krzywa $C$ z prostą. Taka prosta może mieć równanie postaci $v=\alpha u+\beta$ dla $\alpha ,\beta \in \mathbb{R}.$ Wstawiając tę zależność do $\text{(2)}$, dostaniemy wielomian zmiennej $u,$ którego początkowe wyrazy wyglądają następująco: $$W_{\alpha ,\beta }(u)=({\alpha }^3-3{\alpha }^2-3\alpha +1)u^3$$ $$\begin{array}{}\text{(3)}& +(3{\alpha }^2\beta -3{\alpha }^2-6\alpha \beta -5\alpha -3\beta -3)u^2+(\dots ).\end{array}$$ Jest to wielomian 3 stopnia, który może mieć co najwyżej 3 pierwiastki – oznacza to, że punkty przecięcia są również co najwyżej trzy. Ponadto z podstawowej teorii dotyczącej wielomianów (twierdzenie Bézouta) wynika, że jeśli istnieją dwa różne pierwiastki, to istnieje też trzeci – o ile tylko $\alpha \ne -1,$ gdyż wówczas $\text{(2)}$ degeneruje się do wielomianu stopnia 2. Zatem jeśli prosta przechodząca przez punkty $P$ i $Q$ leżące na $C$ ma nachylenie różne od $-1,$ to przecina krzywą $C$ w jeszcze jednym punkcie $R.$

Zastanówmy się, jak mając współrzędne punktów $P=(u_P,v_P)$ i $Q=(u_Q,v_Q),$ można wyznaczyć współrzędne $(u_R,v_R)$ punktu $R.$ Prosta przechodząca przez punkty $P$ i $Q$ ma równanie $$v={\alpha }^{\prime }u+{\beta }^{\prime },$$gdzie ${\alpha }^{\prime }=\frac{v_P-v_Q}{u_P-u_Q}$ oraz ${\beta }^{\prime }=v_P-{\alpha }^{\prime }{u}_P.$ Liczby $u_P,u_Q,u_R$ są zatem pierwiastkami równania $W_{{\alpha }^{\prime },{\beta }^{\prime }}(u)=0.$ Zgodnie ze wzorami Vièta ich suma jest równa $-\frac{a_2}{a_3},$ gdzie $a_i$ to współczynnik stojący przy $u^i$ w wielomianie $W_{{\alpha }^{\prime },{\beta }^{\prime }}.$ Oba te współczynniki przedstawiliśmy w $\text{(3)}$, co daje nam wzór jawny (choć bardzo skomplikowany) na $u_R$: $$u_R=-\frac{3{\alpha }^{\prime 2}{\beta }^{\prime }-3{\alpha }^{\prime 2}-6{\alpha }^{\prime }{\beta }^{\prime }-5{\alpha }^{\prime }-3{\beta }^{\prime }-3}{{\alpha }^{\prime 3}-3{\alpha }^{\prime 2}-3{\alpha }^{\prime }+1}-u_P-u_Q$$ i dalej $v_R={\alpha }^{\prime }{u}_R+{\beta }^{\prime }.$ Z powyższego wzoru wynika, że jeśli liczby $u_P,v_P,u_Q,v_Q$ są wymierne, to liczby $u_R,v_R$ również.