Przygotował Dominik BUREK
Liczba całkowita \(n\) jest taka, że równanie \[x^2 + y^2 + z^2 - xy - yz - zx = n\] ma rozwiązanie w liczbach całkowitych \(x,\) \(y\) i \(z.\) Udowodnić, że równanie \[x^2 + y^2 - xy = n\] ma rozwiązanie w postaci pary liczb całkowitych \(x,y.\)
Znaleźć wszystkie liczby całkowite dodatnie \(n,\) dla których istnieją takie parami różne liczby całkowite dodatnie \(a_{1},\) \(a_{2},\) \(\ldots,\) \(a_{n},\) że liczba \[\frac{a_1}{a_2}+\frac{a_2}{a_3}+\ldots + \frac{a_n}{a_1}\] jest całkowita.
Dla \(n=1,\) biorąc dowolną liczbę całkowitą dodatnią \(a_{1},\) mamy \(\frac{a_{1}}{a_{1}}=1.\)
Dla \(n\geq 3\) rozważmy liczby \[a_{i}=(n-1)^{i- 1}\ \ \ (i=1,\ldots,n).\] Wtedy \[\begin{aligned} &\frac{a_1}{a_2}+\frac{a_2}{a_3}+\ldots + \frac{a_n}{a_1} =\\ &=(n-1)\cdot \frac{1}{n-1}+(n-1)^{n- 1}=\\ &=1+ (n-1)^{n-1}. \end{aligned}\]
Załóżmy teraz, że istnieją dwie różne liczby całkowite dodatnie \(a_1\) i \(a_2\) takie, że suma \(\frac{a_1}{a_2}+\frac{a_2}{a_1}\) jest całkowita. Niech \(a_1 =kd,\) \(a_2 =\ell d,\) gdzie \(d\geq 1\) oraz \(\gcd(k,\ell)=1.\) Wtedy \[\frac{kd}{\ell d}+\frac{\ell d}{kd}=\frac{k^2+\ell^2}{k \ell}\] jest liczbą całkowitą, co oznacza, że \(k\ell \mid k^{2}+\ell^{2}.\) W szczególności \(k\mid \ell^{2},\) więc \(k=1,\) gdyż \(\gcd(k,\ell)=1.\) Podobnie \(\ell=1,\) skąd \(a_{1}=a_{2}\) – sprzeczność.
Dana jest liczba całkowita dodatnia \(n.\) Na szachownicy \(2n\times 2n\) w taki sposób rozmieszczono \(2n\) wież, aby żadne dwie z nich nie znajdowały się w tym samym rzędzie lub w tej samej kolumnie. Następnie tablicę przecięto wzdłuż linii rozdziału pól na dwie spójne części symetryczne do siebie względem środka tablicy. Jaka jest maksymalna liczba wież, które mogą znajdować się w jednej z takich części?
Uwaga: Fragment tablicy nazwiemy spójnym, jeśli jest możliwe przejście w obrębie tego fragmentu między dowolnymi jego polami, za każdym razem przechodząc do pól sąsiadujących bokiem.
Pokażemy najpierw, że nie jest możliwe, aby wszystkie wieże znalazły się w jednej części. Zauważmy na początku, że w każdym wierszu oraz kolumnie znajduje się dokładnie jedna wieża. Niech \(A,\) \(B,\) \(C,\) \(D\) będą kolejnymi narożnikami szachownicy. Z symetrii wynika, że pola \(A\) i \(C\) muszą należeć do różnych części, tak samo jak \(B\) i \(D.\) Oznacza to, że albo \(A\) i \(B,\) albo \(A\) i \(D\) leżą w jednej części, a pozostałe dwa narożniki znajdują się w drugiej części.
Bez straty ogólności załóżmy, że narożniki \(A\) i \(B\) leżą w tej samej części. Wtedy wszystkie pola między nimi również muszą leżeć w tej części. Istotnie, jeśli pole \(X\) leży w części drugiej, to istnieje pewna ścieżka z \(X\) do \(C,\) a ponadto w części pierwszej znajduje się jeszcze ścieżka z \(A\) do \(B.\) Wtedy te ścieżki dzielą wspólne pole, co jest niemożliwe.
Oznacza to, że cały bok \(A\)-\(B\) szachownicy leży w pierwszej części, a zatem jedna z wież także. Dokładnie tak samo dowodzimy, że w drugiej części także znajduje się co najmniej jedna wieża. Oznacza to, że w jednej części nie mogą znajdować się wszystkie wieże.
Następujący przykład pokazuje odpowiedni sposób podziału szachownicy i rozmieszczenia na niej \(2n-1\) wież.
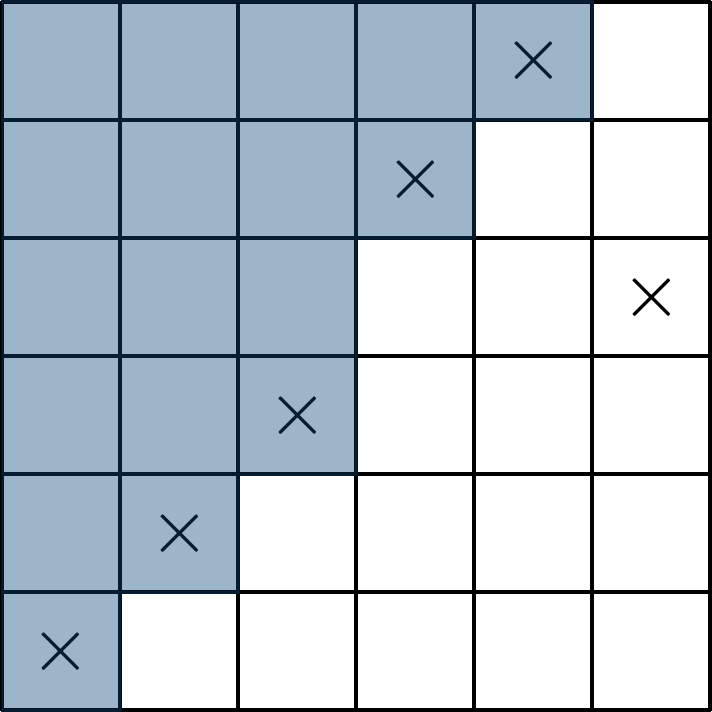
Wieże znajdują się na polach \((i,i)\) dla \(i\leq n,\) \((i,i+1)\) dla \(n<i\leq 2n-1\) oraz na polu \((2n,n+1).\)
Przygotował Andrzej MAJHOFER
Kropla nieściśliwej cieczy została pobudzona do małych drgań polegających na zmianach kształtu względem kształtu sferycznego. Jak częstość \(f\) tych drgań zależy od napięcia powierzchniowego cieczy \(\gamma,\) jej gęstości \(\rho\) oraz promienia kropli \(r\)?
Metoda ,,drgającej kropli” jest stosowana do wyznaczania współczynnika napięcia powierzchniowego cieczy, np. ciekłych metali. Pomiar szybkości tłumienia drgań pozwala dodatkowo, w tym samym pomiarze, wyznaczyć także lepkość cieczy.
W jaki sposób Newton, na podstawie znanych w jego czasach rozmiarów wielkich półosi orbit i okresów obiegu Ziemi wokół Słońca, Księżyca wokół Ziemi oraz Callisto wokół Jowisza, mógł wyznaczyć stosunek masy Słońca \(M_S\) i masy Jowisza \(M_J\) do masy Ziemi \(M_Z\)?
Potrzebne dane: okres obiegu Ziemi \(T_Z = 365{,}26\) dni, wielka półoś orbity
\(a_z = 149{,}598\cdot 10^6\) km; okres obiegu Księżyca \(T_K = 27{,}32\) dni, wielka półoś \(a_K = 0{,}384\cdot 10^6\) km; okres obiegu Callisto \(T_C = 16{,}69\) dni, półoś \(a_C = 1{,}883\cdot 10^6\) km – wartości znane współcześnie.