Redaguje Marcin E. KUCZMA
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
891 (\(WT = 1{,}36\)) i 892 (\(WT = 2{,}14\))
z numeru 12/2024
Krzysztof Zygan Lubin 43,39 Andrzej Kurach Ryjewo 43,21 Janusz Olszewski Warszawa 40,67 Michał Warmuz Żywiec 40,04 Marcin Kasperski Warszawa 39,14 Andrzej Daniluk Warszawa 37,89 Grzegorz Wiączkowski 36,58 Marek Spychała Warszawa 35,24 Marian Łupieżowiec Gliwice 34,85 Krzysztof Kamiński Pabianice 34,36 Piotr Wiśniewski Warszawa 33,97 Krzysztof Maziarz Londyn 33,32
Rozwiązania zadań z numeru 3/2025
Przypominamy treść zadań:
897. Czworokąt wypukły \(ABCD\) ma obwód długości \(p\) oraz przekątne długości \(m\) i \(n.\) Punkt \(E\) jest czwartym wierzchołkiem równoległoboku \(ABCE.\) Udowodnić, że \({DE\le{p-m-n}}.\)
898. Wyznaczyć wszystkie pary liczb naturalnych \({m,n\ge1},\) dla których wielomian \({W(x)=x^m+x^n+1}\) jest podzielny przez trójmian \({T(x)=x^2+x+1}.\)
897. Na płaszczyźnie zespolonej punkty \(A,B,C,D,E\) są reprezentowane przez liczby \(a,b,c,d,e\) (położenie punktu 0 nie ma znaczenia). Mamy udowodnić nierówność \({p\ge{m+n+DE}},\) czyli \[|a-b|+|b-c|+|c-d|+|d-a|\ge|a-c|+|b-d|+|d-e|. \tag{1}\] Przyjmijmy oznaczenia: \({a-b=x},\) \({b-c=y},\) \({c-d=z}.\) Wówczas \[a-d=x+y+z;\ \ \ \ a-e=y\] (skorzystaliśmy z założenia, że \(ABCE\) to równoległobok); \[e-d=(a-d)-(a-e)=x+z.\] Wprowadzamy te oznaczenia do (1) i dostajemy do udowodnienia nierówność \[|x|+|y|+|z|+|x+y+z|\ge|x+y|+|y+z|+|z+x|. \tag{2}\] Wobec jednorodności można przyjąć, że \({x+y+z=1}\) (ta suma nie może być zerowa, bo \({a\ne{d}}\)). To sprowadza nierówność (2) do postaci \[|x|+|y|+|z|+1\ge|1-z|+|1-x|+|1-y|.\] Obie strony są nieujemne. Podnosząc je do kwadratu, uzyskamy (do dowodu) nierówność równoważną: \[\sum|x|^2+2\sum|xy|+2\sum|x|+1\ge\sum|1-x|^2+2\sum|(1-x)(1-y)| \tag{3}\] (symbol \(\sum\) oznacza sumowanie cykliczne w zmiennych \(x,y,z\)). Zauważając, że \({(1-x)(1-y)=xy+z},\) przekształcamy (3) do postaci kolejno równoważnych: \[\begin{aligned} \sum|x|^2+2\sum|xy|+2\sum|z|+1 & \ge\sum(1-2{\rm{Re}}\,x+|x|^2)+2\sum|xy+z|; \\ 2\sum(|xy|+|z|)+1 & \ge3-2\sum{\rm{Re}}\,x+2\sum|xy+z|; \\ 2\sum(|xy|+|z|-|xy+z|) & \ge2(1-\sum{\rm{Re}}\,x). \\ \end{aligned}\] Ostatnia nierówność jest banalnie prawdziwa: lewa strona jest nieujemna, a prawa jest równa zeru, bo \({\sum{x}=1}.\) To dowodzi słuszności nierówności we wszystkich wcześniejszych postaciach, więc i tezy (1).
[Uwaga. Nierówność (2) zachodzi dla każdej trójki liczb zespolonych, jak pokazuje przeprowadzony rachunek. Kontekst geometryczny służy jako jej interpretacja. Zbędne jest założenie wypukłości czworokąta; to może być dowolna linia łamana \(ABCD,\) nawet z fragmentami pokrywającymi się. Proponujemy Czytelnikom, jako ćwiczenie, rozpoznanie sytuacji, gdy (2) staje się równością.]
898. Trójmian \(T\) rozkłada się na czynniki liniowe \({T(x)=(x-\alpha)(x-\beta)},\) gdzie \({\alpha=-\frac12+\frac12\sqrt3\,i},\) \({\beta=-\frac12-\frac12\sqrt3\,i}.\) Zatem \(W\) dzieli się przez \(T\) wtedy i tylko wtedy, gdy dzieli się przez \({(x-\alpha)}\) i \({(x-\beta)}\); równoważnie (tw. Bézout) – gdy \[W(\alpha)=0,\ \ \ \ W(\beta)=0. \tag{4}\] Istotne są reszty z dzielenia \(m,n\) przez 3: \[\alpha^m= \begin{cases} 1 & \text{gdy $m\equiv0$~(mod~3),} \\ \alpha & \text{gdy $m\equiv1$~(mod~3),} \\ \beta & \text{gdy $m\equiv2$~(mod~3),} \end{cases} \ \ \ \hbox{i~podobnie}\;\alpha^n,\beta^m,\beta^n. \tag{5}\] Jeśli \(m\) dzieli się przez 3, to \({W(\alpha)=\alpha^m+\alpha^n+1=2+\alpha^n\ne0},\) warunek (4) nie jest spełniony; podobnie wykluczamy przypadek, w którym \(n\) dzieli się przez 3. Pozostają \({m,n\equiv1,2}\) (mod 3). Łatwo teraz ze wzoru (5) uzyskać ostateczną odpowiedź: warunek (4) (równoważny podzielności wielomianu \(W\) przez \(T\)) jest spełniony wtedy i tylko wtedy, gdy \({m\equiv1,\;n\equiv2}\) (mod 3) lub \({m\equiv2,\;n\equiv1}\) (mod 3).
Redaguje Elżbieta ZAWISTOWSKA
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
788 (\(WT=2{,}37\)), 789 (\(WT=1{,}99\))
z numeru 12/2024
Tomasz Wietecha (Tarnów) 18 – 44+3,02 Jacek Konieczny (Poznań) 41,11 Jan Zambrzycki (Białystok) 4 – 31,23 Andrzej Nowogrodzki (Chocianów) 3 – 29,48
Rozwiązania zadań z numeru 3/2025
Przypominamy treść zadań:
794. Z soczewki skupiającej o ogniskowej \(f=50\) cm i średnicy \(D=5\) cm wycięto środkowy pasek o szerokości 5 mm, a pozostałe części złożono ze sobą (rys. 1). W odległości \(x=75\) cm od soczewki umieszczono punktowe źródło światła monochromatycznego \(S.\) Korzystając z przybliżenia małych kątów, znaleźć maksymalną liczbę prążków obrazu interferencyjnego, jaka może powstać na ekranie za soczewką. Długość fali świetlnej \(\lambda =5\cdot 10^{-7}\,\)m.
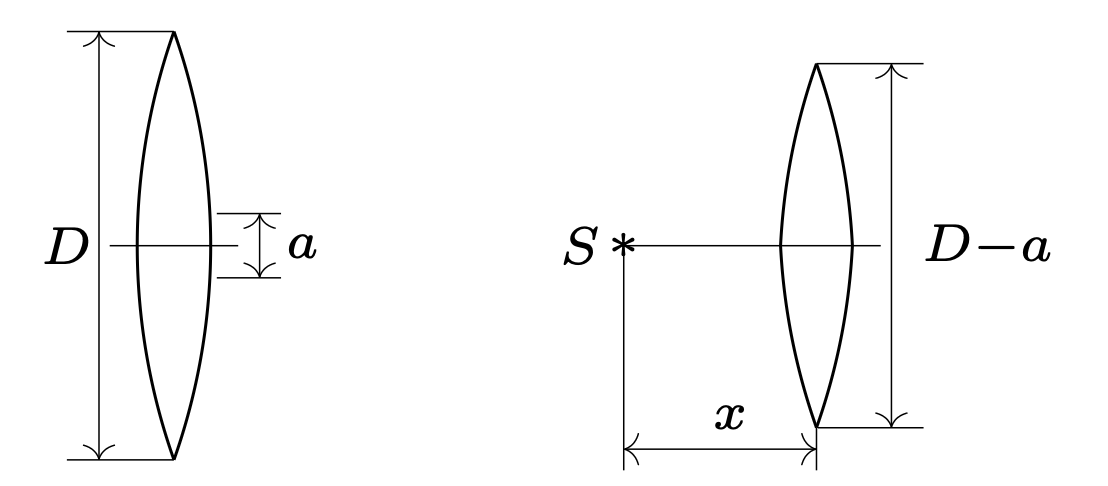 Rys. 1
Rys. 1
795. Izolowaną metalową, początkowo nienaładowaną płytkę oświetlano w czasie \(\tau\) światłem nadfioletowym. W wyniku tego z płytki wyleciała chmura elektronów, których prędkość początkowa była prostopadła do płytki i miała wartość \(v_0.\) Całkowita liczba elektronów, które wyleciały z jednostki powierzchni, wynosi \(n,\) elektron ma ładunek \(e\) i masę \(m.\) Znaleźć grubość chmury \(h\) po czasie \(t\) od zakończenia naświetlania (rys. 2).
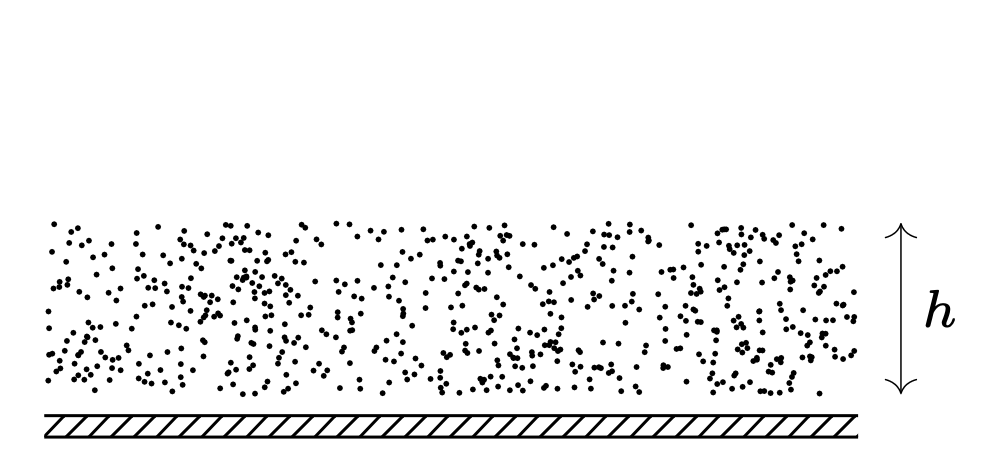 Rys. 2
Rys. 2
794. Soczewka z wyciętym paskiem dzieli światło ze źródła \(S\) na dwie wiązki. Tam, gdzie wiązki przecinają się, możemy obserwować prążki interferencyjne.
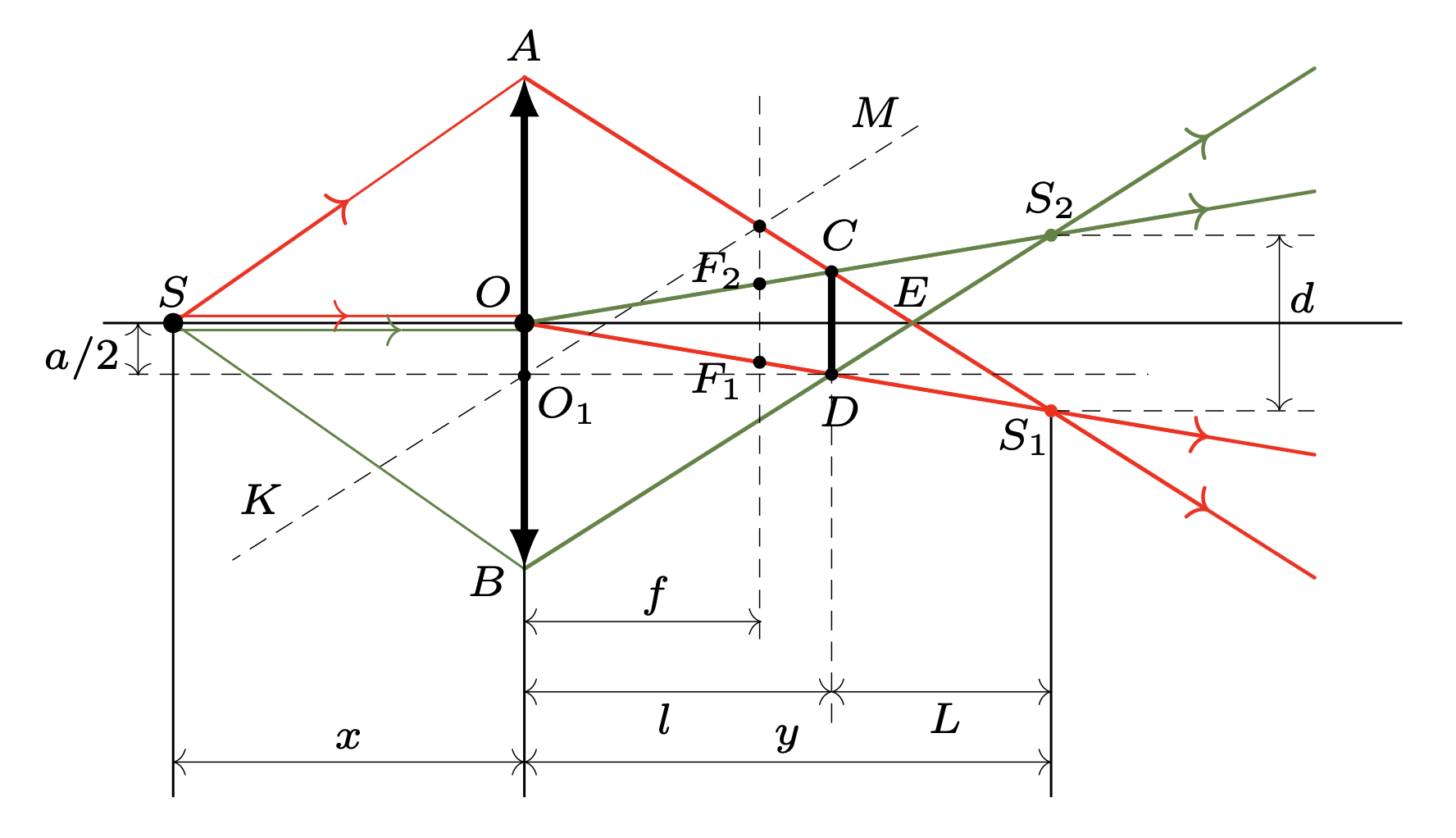
Górna część obciętej soczewki daje obraz \(S_{1}\) źródła \(S\) (promień \(AS_{1}\) przecina równoległy do \(SA\) promień \(KO_{1}\) w punkcie \(M\) płaszczyzny ogniskowej). Obraz \(S_{2}\) źródła w dolnej części soczewki leży po drugiej stronie osi układu i jest spójny z \(S_{1}\). Obszar przecięcia wiązek znajduje się między soczewką oraz punktem \(E\) przecięcia promieni \(AS_{1}\) i \(BS_{2}\). W odległości \(l\) od soczewki przekrój tego obszaru jest największy.
W przybliżeniu małych kątów w odległości \(L\) od odcinka \(S_{1}S_{2}\) możemy obserwować \(N = |CD|/\mathrm{\Delta}x\) jasnych prążków, gdzie \({\Delta}x = \lambda L/d\) jest szerokością prążka, a \(d\) to długość odcinka \(S_{1}S_{2}\).
Gdy płaszczyzna obserwacji oddala się od soczewki, szerokość prążków maleje. Szerokość obszaru przecięcia wiązek rośnie przed płaszczyzną \(CD\), a następnie maleje szybciej niż szerokość prążka. Maksymalną liczbę prążków obserwujemy więc w płaszczyźnie \(CD\).
Z podobieństwa trójkątów \(OCD\) i \(OF_{1}F_{2}\): \[|CD| = al/f,\ \ \ N = ald/f\lambda L.\] Z podobieństwa trójkątów \(S_{1}S_{2}C\) i \(AOC\): \[l/L = (D - a)/2d.\] Szukana maksymalna liczba prążków na ekranie: \[N = a(D - a)/2f\lambda = 450.\]
795. Płytka i chmura elektronów tworzą kondensator płaski. Pole między okładkami ma natężenie \(E = en/\varepsilon_{0}\). Na górnej granicy chmury prędkość elektronów wynosi \(v_{0}\), na dolnej ich przyspieszenie ma wartość \(a = eE/m = e^{2}n/\left( m\varepsilon_{0} \right)\). Do chwili \(t\) górne elektrony przebędą drogę \(h_{1} = v_{0}(\tau + t)\), a dolne \(h_{2} = v_{0}t - at^{2}/2\), stąd szukana grubość chmury: \[h = h_{2} - h_{1} = v_{0}\tau + e^{2}nt^{2}/ 2m\varepsilon_{0} , \text{ gdy }t < 2v_{0}/a.\] Po czasie \(t_{0} = 2v_{0}/a\) dolne elektrony zaczną wracać na płytkę, a górne nie zmienią swego ruchu, zatem dla czasu \(t \geq 2v_{0}/a\ \) grubość chmury \(h = v_{0}(t + \tau)\).
