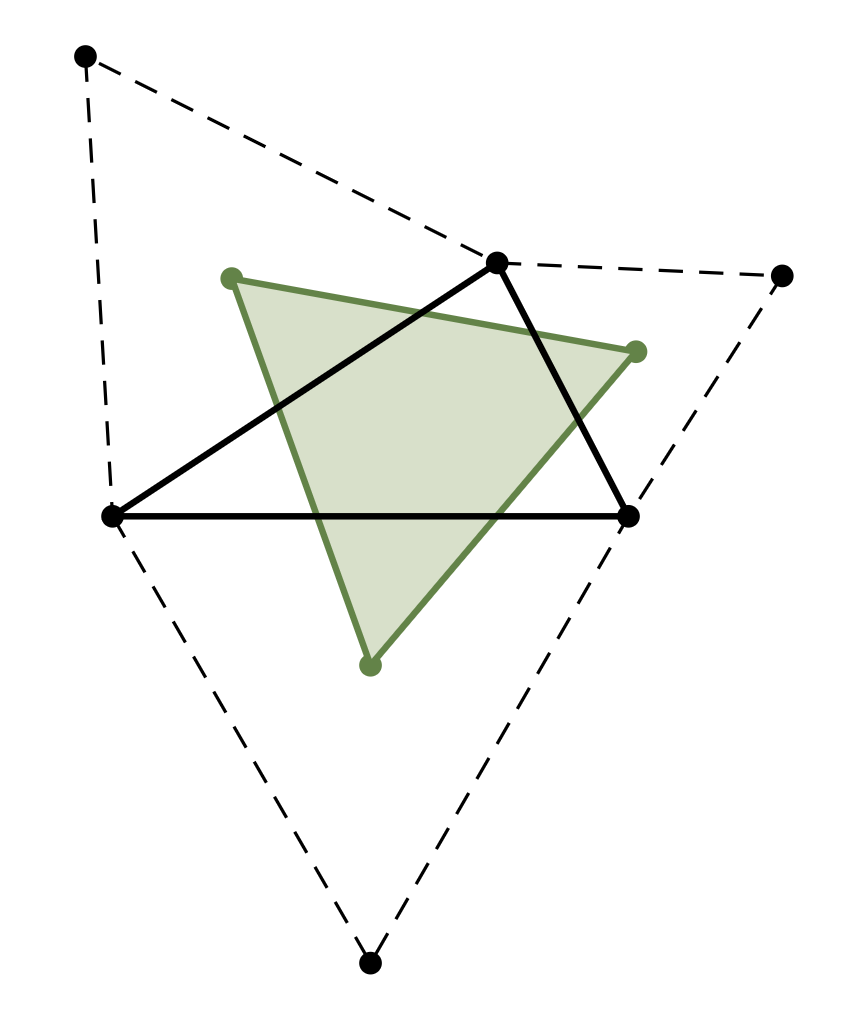
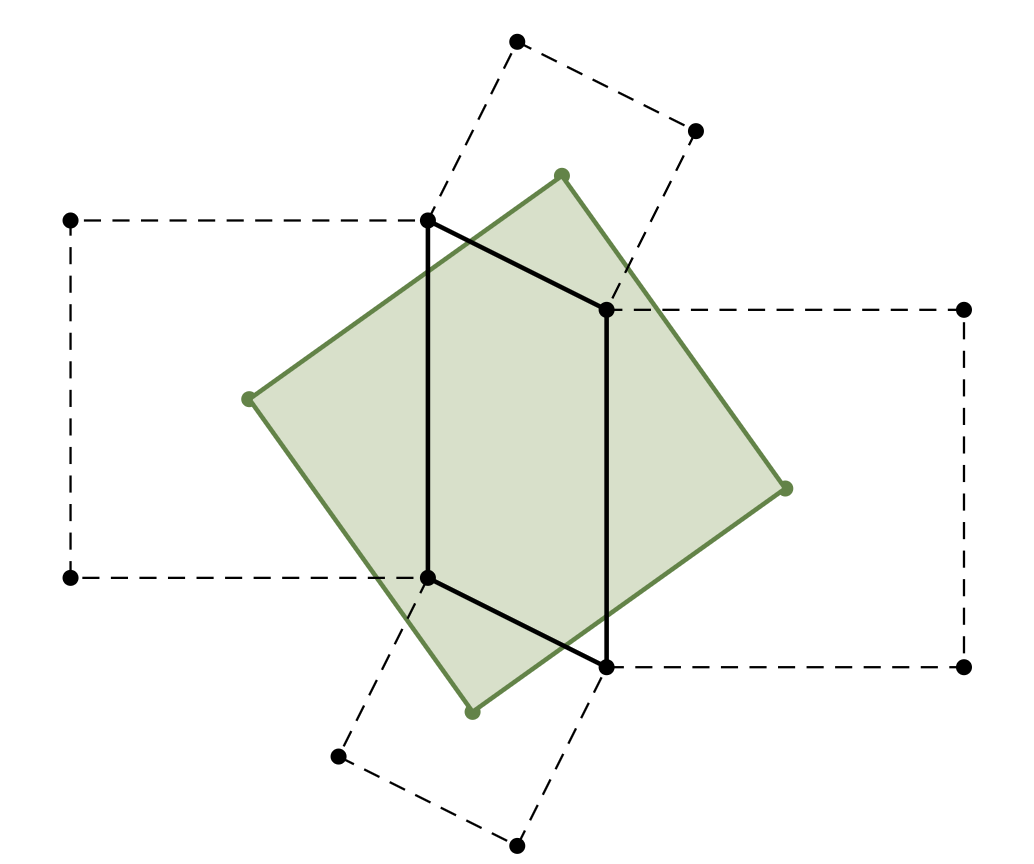
Jednym z twierdzeń niemających żadnego udokumentowanego związku z Napoleonem Bonaparte jest tzw. twierdzenie Napoleona:
Środki trójkątów równobocznych zbudowanych na zewnątrz boków danego trójkata są wierzchołkami trójkąta równobocznego.
Pierwszy znany zapis tego twierdzenia pojawił się kilka lat po śmierci francuskiego cesarza – w 1826 roku przedstawił je angielski matematyk William Rutheford, jednak nie powołał się na żadne źródło.
Zarówno w powyższym twierdzeniu, jak i w całym tekście, za środek wielokąta foremnego uznajemy punkt równoodległy od wszystkich jego wierzchołków.
Twierdzenie Napoleona niejednokrotnie było przytaczane na łamach Delty – wspominają o nim Joanna Jaszuńska w \(\Delta_{09}^{5}\) i w \(\Delta_{15}^{12}\) oraz Bartłomiej Bzdęga w \(\Delta_{19}^{9}\). Tym razem przyjrzymy się jednemu z możliwych kierunków uogólnień tego twierdzenia: na zewnątrz boków \(n\)-kąta będziemy budować \(n\)-kąty foremne.
Czy prawdą jest, że łącząc środki kwadratów budowanych na zewnątrz boków dowolnego czworokąta, otrzymamy kwadrat? Okazuje się, że niekoniecznie: wystarczy rozpatrzyć dowolny trapez prostokątny o różnych podstawach:
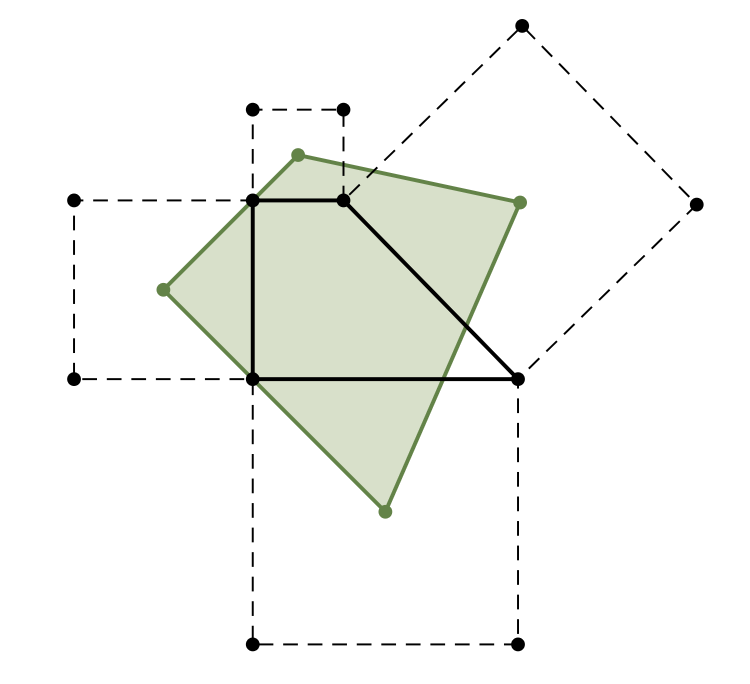
Czy można zatem sformułować interesujące nas uogólnienie twierdzenia Napoleona dla czworokątów? Z pomocą przychodzi nam Victor Thébault, żyjący w pierwszej połowie XX wieku matematyk francuski, znany przede wszystkim ze sformułowania setek oryginalnych problemów z zakresu teorii liczb i geometrii (publikowanych przeważnie w American Mathematical Monthly). Thébault jest autorem następującego spostrzeżenia:
Środki kwadratów zbudowanych na zewnątrz boków danego równoległoboku są wierzchołkami kwadratu.
Obserwacja Thébaulta nie daje pełnego obrazu sytuacji dla figur z czterema bokami. Czy istnieją czworokąty niebędące równoległobokami, mające rozpatrywaną własność? Okazuje się, że nie – potraktujemy ten fakt jako wniosek z dużo ogólniejszego twierdzenia Napoleona–Barlottiego:
Środki \(n\)-kątów foremnych zbudowanych na zewnątrz boków \(n\)-kąta \(F\) są wierzchołkami \(n\)-kąta foremnego wtedy i tylko wtedy, gdy \(F\) jest afinicznym obrazem \(n\)-kąta foremnego.
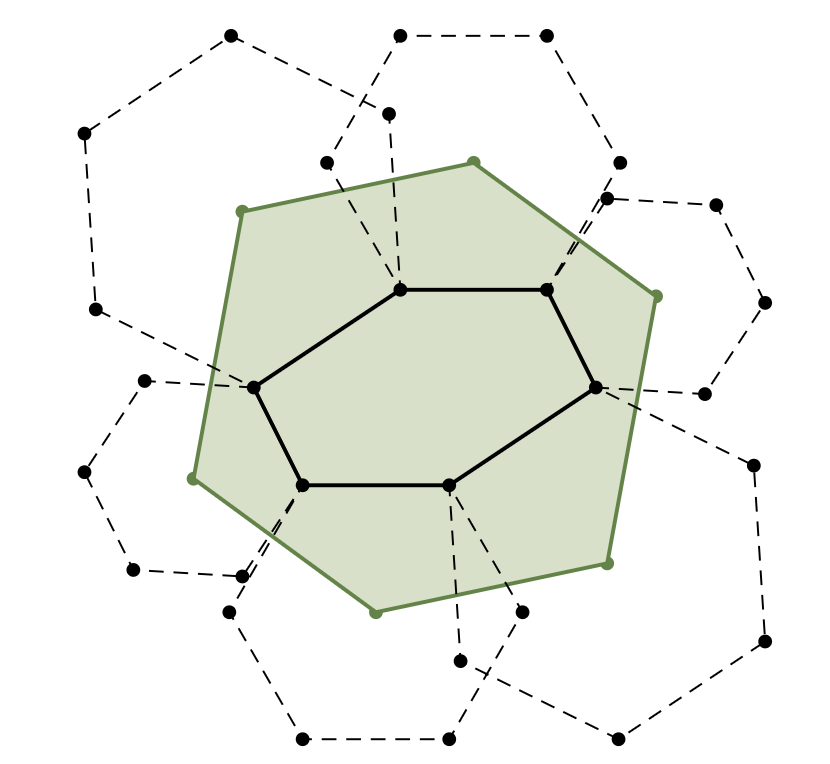
Przekształcenie afiniczne to, z grubsza, przekształcenie zachowujące równoległość prostych oraz proporcje między długościami odcinków na bokach równoległych. Przykładowo afinicznym obrazem kwadratu może być jedynie równoległobok.
Na koniec dodajmy, że oczywiście nie jest to jedyne możliwe uogólnienie twierdzenia Napoleona. Można na przykład, jak Jha-Savaran czy Dao Than Oai, budować trójkąty równoboczne na bokach sześciokątów (które w zdegenerowanym przypadku stają się trójkątami, dając twierdzenie Napoleona). Szczególnie pięknym uogólnieniem jest twierdzenie Petra–Douglassa–Neumanna. Jednak są to zagadnienia na zupełnie inną opowieść…
Znakomity materiał dotyczący twierdzenia Petra–Douglassa–Neumanna można zobaczyć na youtube’owym kanale Mathologer: Petr’s miracle: Why was it lost for 100 years?