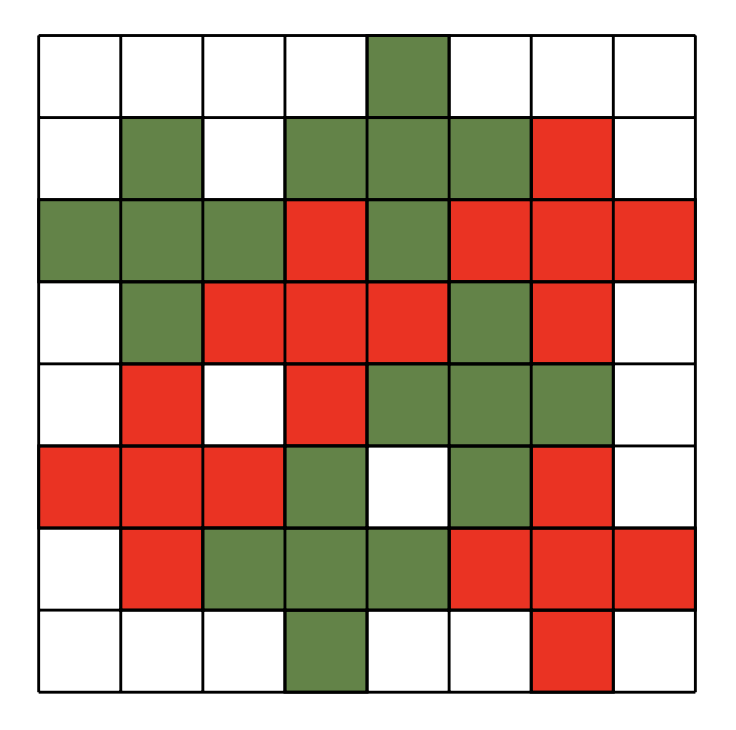
Rozstrzygnąć, jaka jest największa możliwa liczba rozłącznych pentomino w kształcie plusa (rys. 1), które można położyć na szachownicy \(8 \times 8\) tak, by boki pentomino były równoległe do boków szachownicy.
Rys. 1
Zauważmy, że pentomino mogą zająć jedynie \(2\) spośród \(8\) pól w dolnym rzędzie. Istotnie, każde pentomino może zająć tylko jedno pole w tym rzędzie, więc gdyby zajmowały one \(3\) pola w dolnym rzędzie, to w rzędzie wyżej byłoby zajętych \(9\) pól – sprzeczność.
Oznacza to, że w sumie mogą być zajęte co najwyżej \(6^2 + 4 \cdot 2 = 44\) pola (\(6^2\) wewnętrznych pól i po \(2\) na każdej z czterech krawędzi). Każde pentomino zajmuje \(5\) pól, czyli jest co najwyżej \(\bigl\lfloor \frac{44}{5} \bigr\rfloor = 8\) pentomino.
Z drugiej strony nietrudno narysować \(8\) rozłącznych pentomino na szachownicy \(8\times 8.\)
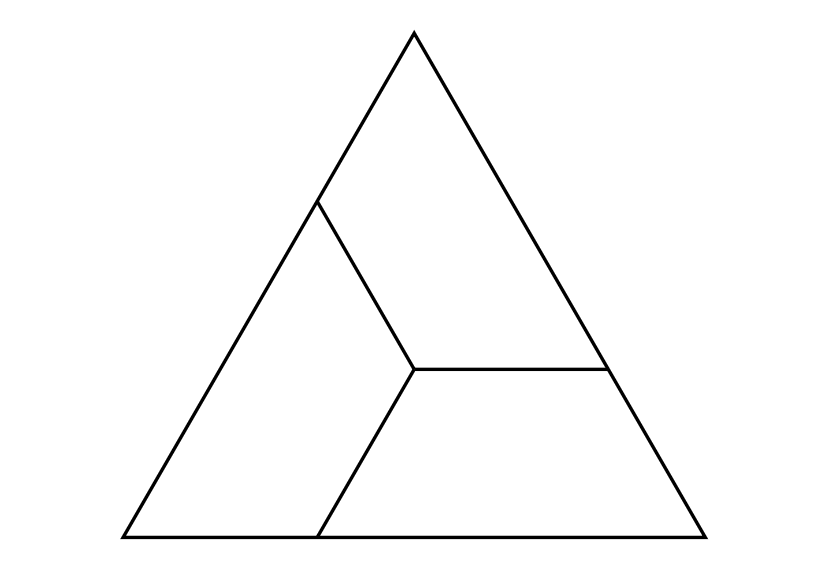
Udowodnić, że dowolny wielokąt wypukły można podzielić na trapezy równoramienne.
Nietrudno znaleźć żądany podział w przypadku, gdy \(ABC\) jest równoboczny. Wystarczy ze środka trójkąta poprowadzić trzy półproste równoległe do jego boków.
Jeśli \(\measuredangle BAC > 60^{\circ},\) to możemy go z łatwością podzielić na trójkąt równoboczny i 4 trapezy równoramienne.
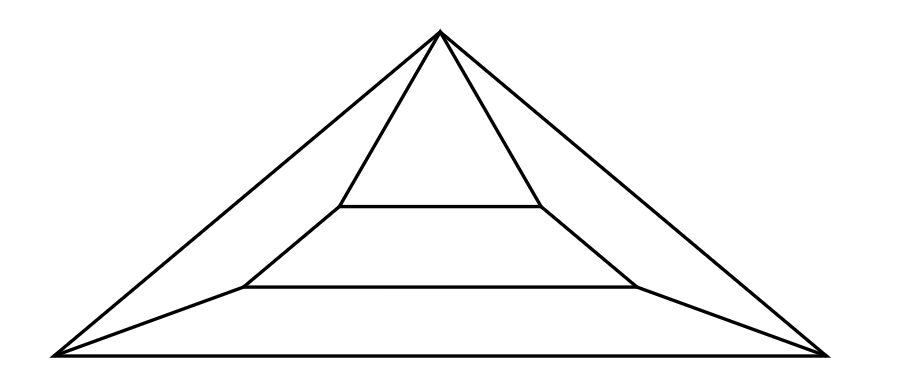
Jeśli natomiast \(\measuredangle BAC<60^{\circ},\) to łącząc wierzchołki tego trójkąta z jego środkiem okręgu opisanego \(O,\) uzyskujemy trzy trójkąty, z których dwa są rozwartokątne równoramienne (dla nich stosujemy podział z poprzedniego akapitu) oraz trójkąt równoramienny \(BOC\) (\(OB=OC\)) z kątem przy wierzchołku \(O\) równym \(2\measuredangle BAC.\) Dla tego trójkąta stosujemy wielokrotnie procedurę opisaną w poprzednim lub niniejszym akapicie.
Dany jest ciąg \((a_n)_{n \geq 1}\) zdefiniowany przez warunki \(a_1 = 1\) oraz \(a_{2n} = a_n\) i \(a_{2n+1} = a_n + a_{n+1}\) dla \(n\geq 1.\) Udowodnić, że każda liczba wymierna dodatnia występuje dokładnie raz w ciągu \(\bigl(\frac{a_n}{a_{n+1}}\bigr)_{n \geq 1}.\)
Przypuśćmy teraz, że istnieje taka liczba wymierna, która występuje więcej niż raz w tym ciągu. Wybierzmy taką liczbę \(p/q,\) przy czym niech \(p+q\) będzie najmniejsze. Bez straty ogólności przyjmijmy, że \(q > p.\) Łatwo sprawdzić, że w ciągu \((a_n)\) wyrazy o nieparzystych indeksach są większe od obu swoich sąsiadów. Możemy zatem przyjąć: \(a_{2n} = p,\) \(a_{2n+1} = q\) oraz \(a_{2m} = p, a_{2m+1} = q\) dla pewnych \(m,n\geq 1.\) Wówczas \(a_n = p,\) \(a_{n+1} = q-p\) oraz \(a_m = p,\) \(a_{m+1} = q-p.\) Oznacza to, że liczba \(p/(q-p)\) również występuje wielokrotnie w naszym ciągu oraz \(p + (q-p) < p + q,\) co jest sprzeczne z wyborem pary \((p,q).\)
W naczyniu o kształcie ściętego stożka (rys. 2) początkowo znajduje się jednorodna mieszanina dwóch cieczy o różnych gęstościach. Po pewnym czasie ciecze rozdzielają się i lżejsza (o mniejszej gęstości) zbiera się w górnej części naczynia. Czy w wyniku tego procesu zmienia się ciśnienie na dno naczynia? Przyjmujemy, że całkowita objętość cieczy przed i po ich rozdzieleniu pozostaje niezmieniona. Przyspieszenie ziemskie wynosi \(g.\)
Rys. 2
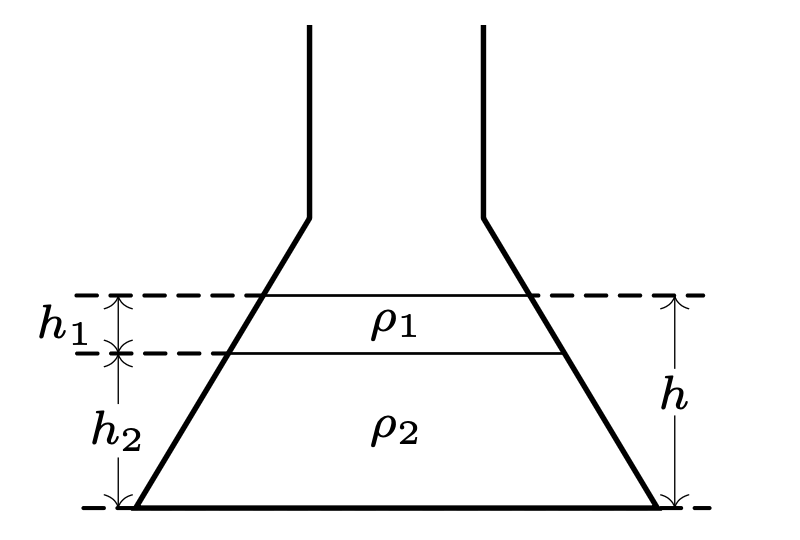 Po rozdzieleniu ciecz o większej gęstości, \(\rho_2,\) wypełnia dolną część naczynia do wysokości \(h_2,\) a nad nią powstaje warstwa o grubości \(h_1\) cieczy o gęstości \(\rho_1 < \rho_2.\) Mamy oczywiście \(h_1 + h_2 = h.\) Przyjmijmy, że objętości cieczy wynoszą, odpowiednio, \(V_1\) i \(V_2.\) Gęstość mieszaniny przed rozdzieleniem wynosi:
\[\rho = \frac{\rho_1V_1 + \rho_2V_2}{V_1 + V_2},\]
a ciśnienie na dno:
\[p_p = gh\rho .\]
Po rozdzieleniu cieczy ciśnienie na dno wynosi:
\[p_k = gh_1\rho_1 +gh_2\rho_2.\]
Po prostych obliczeniach otrzymujemy:
\[p_p - p_k = g(\rho_2 - \rho_1)\frac{hV_2 - h_2(V_1 + V_2)}{V_1 + V_2}.\]
Niech promień wewnętrznego przekroju naczynia na wysokości \(h\) wynosi \(r,\) na wysokości powierzchni rozdziału cieczy \(r_1 > r,\) a dna \(R > r_1.\)
Korzystając ze wzoru na objętość ściętego stożka, otrzymujemy:
\[hV_2 - h_2(V_1 + V_2) = hh_2((Rr_1 + r_1^2 -Rr -r^2) > 0,\]
a więc podczas rozdzielania cieczy (frakcjonowania) maleje ciśnienie na dno naczynia o kształcie ściętego stożka. Opisany proces ma miejsce np. podczas
zbierania się śmietanki na powierzchni mleka.
Po rozdzieleniu ciecz o większej gęstości, \(\rho_2,\) wypełnia dolną część naczynia do wysokości \(h_2,\) a nad nią powstaje warstwa o grubości \(h_1\) cieczy o gęstości \(\rho_1 < \rho_2.\) Mamy oczywiście \(h_1 + h_2 = h.\) Przyjmijmy, że objętości cieczy wynoszą, odpowiednio, \(V_1\) i \(V_2.\) Gęstość mieszaniny przed rozdzieleniem wynosi:
\[\rho = \frac{\rho_1V_1 + \rho_2V_2}{V_1 + V_2},\]
a ciśnienie na dno:
\[p_p = gh\rho .\]
Po rozdzieleniu cieczy ciśnienie na dno wynosi:
\[p_k = gh_1\rho_1 +gh_2\rho_2.\]
Po prostych obliczeniach otrzymujemy:
\[p_p - p_k = g(\rho_2 - \rho_1)\frac{hV_2 - h_2(V_1 + V_2)}{V_1 + V_2}.\]
Niech promień wewnętrznego przekroju naczynia na wysokości \(h\) wynosi \(r,\) na wysokości powierzchni rozdziału cieczy \(r_1 > r,\) a dna \(R > r_1.\)
Korzystając ze wzoru na objętość ściętego stożka, otrzymujemy:
\[hV_2 - h_2(V_1 + V_2) = hh_2((Rr_1 + r_1^2 -Rr -r^2) > 0,\]
a więc podczas rozdzielania cieczy (frakcjonowania) maleje ciśnienie na dno naczynia o kształcie ściętego stożka. Opisany proces ma miejsce np. podczas
zbierania się śmietanki na powierzchni mleka.
Oszacuj, jakiej średnio energii, \(\varepsilon,\) potrzeba do ,,wyrwania” pojedynczej cząsteczki z powierzchni (ciekłej) wody. Ciepło parowania wody wynosi \({L = 2257}\) J/g, masa atomowa wodoru \(\mu_H = 1\) g, masa atomowa tlenu \(\mu_O = 16\) g, a stała Avogadro: \(N_A = 6,022\cdot 10^{23}.\)
