Jakiś czas temu (\(\Delta_{22}^{5}\)) w Klubie 44 M pojawiło się zaproponowane przeze mnie zadanie numer \(\left\lfloor 44^4/(4444+4)\right\rfloor\) o następującej treści:
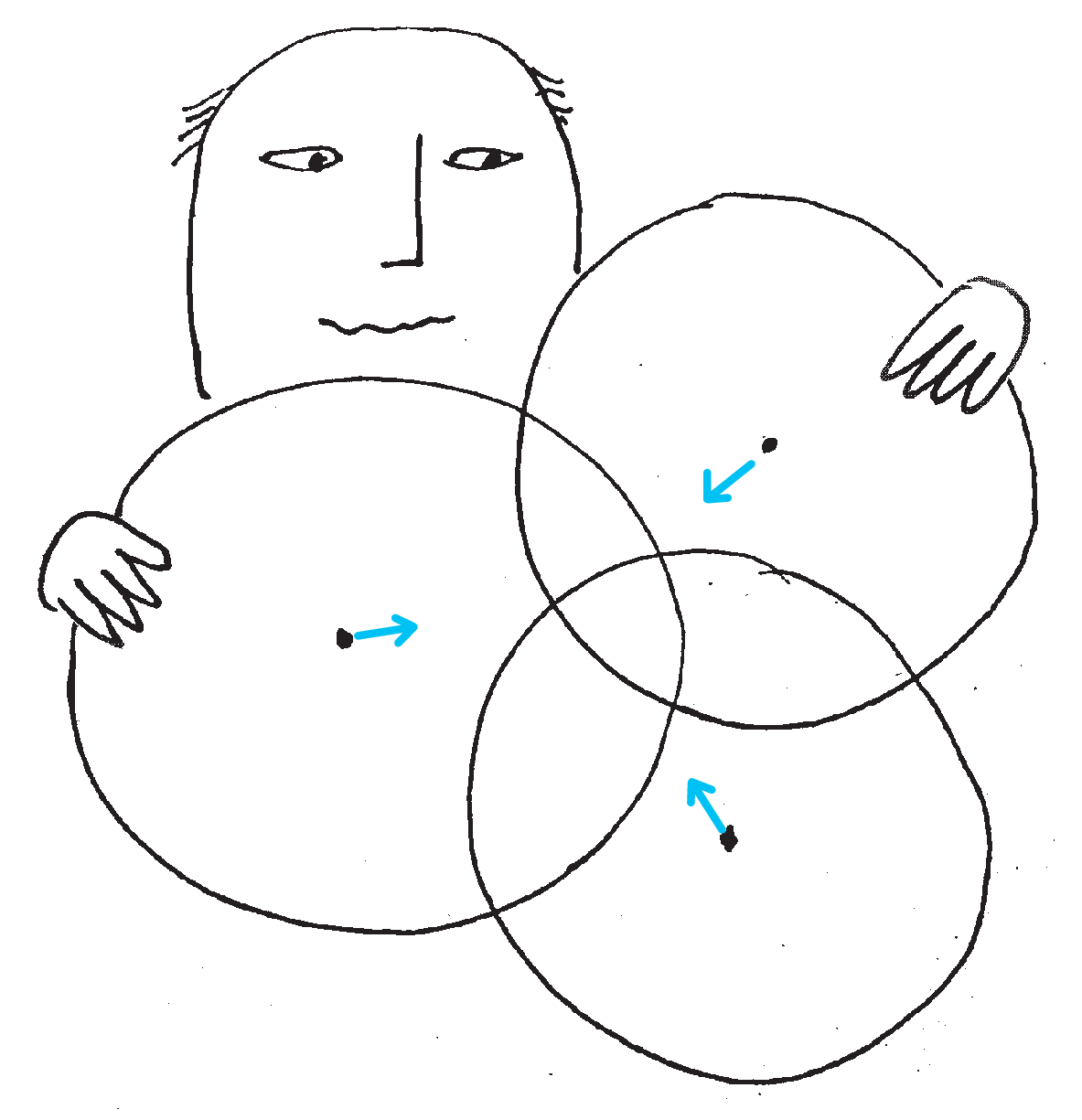
Na płaszczyźnie znajdują się trzy koła o niepustym przecięciu. Przesuwamy każde koło (niezależnie) w taki sposób, że po przesunięciu środki każdych dwóch kół są bliżej siebie niż na początku. Udowodnić, że przesunięte koła nadal mają niepuste przecięcie.
Myślę, że każdemu Czytelnikowi teza tego zadania wydaje się Oczywista, przez duże O. Jeszcze bardziej przekonujący jest rzut oka na kontrapozycję: jeżeli trzy koła mają puste przecięcie i przesuniemy je tak, że ich środki parami się od siebie oddalą, to przesunięte koła muszą mieć „jeszcze bardziej puste” przecięcie. Trywialne, brakuje tylko dowodu.
Zadanie, w narzucającej się ogólniejszej wersji dla zbliżania dowolnej liczby kul w \(\mathbb{R}^n\) odkryłem w zbiorku ćwiczeń [1] do klasycznego podręcznika z optymalizacji wypukłej. Podane tam wskazówki prowadzą do analitycznego rozwiązania z użyciem mnożników Lagrange’a – w końcu ćwiczenia są po to, żeby ćwiczyć techniki przedstawione w książce. Zaintrygowało mnie to i pomyślałem, że warto byłoby poszukać, choćby w dwóch wymiarach, bardziej geometrycznego dowodu. Już na pierwszy rzut oka zresztą widać, że trzy dyski na płaszczyźnie to pierwszy przypadek, w którym teza nie jest za darmo i coś trzeba zrobić. Więc zróbmy. Będziemy się zajmować następującym wariantem, równoważnym oryginalnemu, co Czytelnik bez trudu sprawdzi. (Jako że w tym numerze obchodzimy urodziny ligi zadaniowej, zadań pozostawionych w prezencie dla Czytelnika będzie sporo).
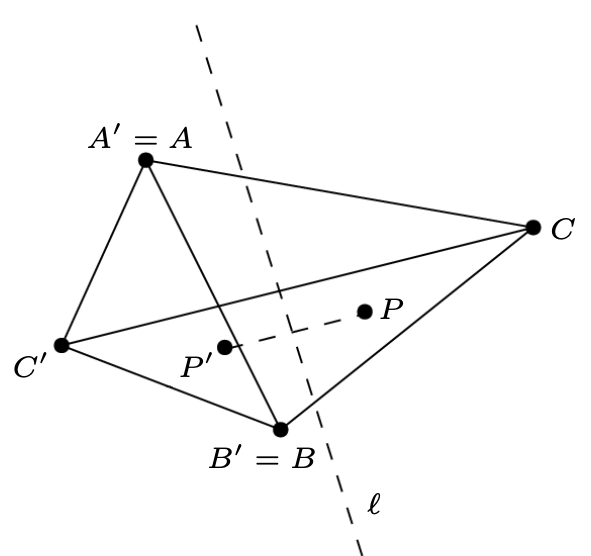
Zadanie 842(bis). Na płaszczyźnie znajdują się dwa trójkąty \(ABC\) i \(A'B'C',\) przy czym ten drugi jest „mniejszy” w następującym sensie: \[|A'B'|\leq |AB|,\ \ \ |B'C'|\leq |BC|,\ \ \ |C'A'|\leq |CA|.\] Wówczas dla dowolnego punktu \(P\) tej płaszczyzny istnieje taki punkt \(P'\) , że \[|P'A'|\leq |PA|,\ \ \ |P'B'|\leq |PB|,\ \ \ |P'C'|\leq |PC|.\] A oto szkic rozwiązania, zaadaptowanego z rozwiązania firmowego (\(\Delta_{22}^{9}\)). Najpierw zauważamy, że wystarczy rozważyć przypadek, gdy liczba \({k=\max\bigl(\frac{|A'B'|}{|AB|},\frac{|B'C'|}{|BC|},\frac{|C'A'|}{|CA|}\bigr)}\) jest równa \(1.\) W przeciwnym razie, tzn. gdy \(k<1,\) wystarczy „rozdmuchać” jednokładnie trójkąt \(A'B'C'\) w skali \(k^{-1},\) wziąć rozwiązanie dla tego trójkąta, przekształcić je przez odwrotną jednokładność o skali \(k,\) i wszystkie pożądane nierówności będą spełnione, nawet z naddatkiem: \(|P'A'|\leq k\cdot |PA|,\) \(|P'B'|\leq k\cdot |PB|,\) \(|P'C'|\leq k\cdot |PC|.\) Niech więc \(k=1,\) czyli bez straty ogólności \[|A'B'|=|AB|,\ \ \ |B'C'|\leq |BC|,\ \ \ |C'A'|\leq |CA|.\] Aplikując izometrię, którą na koniec możemy odwrócić, możemy więc po prostu przyjąć \(A'=A,\) \(B'=B.\) Główną rolę odgrywa teraz symetralna \(\ell\) odcinka \(CC'.\) Z nierówności \[|BC'|=|B'C'|\leq |BC|,\ \ \ |AC'|=|A'C'|\leq |AC|\] wynika, że punkty \(A,B,C'\) leżą po tej samej stronie \(\ell.\) Jeżeli punkt \(P\) też leży po tej stronie, to \(|PC'|\leq |PC|,\) i kładziemy po prostu \(P'=P\): \[|P'A'|=|P'A|=|PA|,\ \ \ |P'B'|=|P'B|=|PB|,\ \ \ |P'C'|=|PC'|\leq |PC|.\] W przeciwnym razie niech \(P'\) będzie obrazem punktu \(P\) w symetrii względem \(\ell\) (rys. 1). Wtedy też jest dobrze, bo prosta \(\ell\) jest również symetralną odcinka \(PP'\) i punkty \(A,B,P'\) leżą po tej samej jej stronie, więc: \[|A'P'|=|AP'|\leq |AP|,\ \ \ |B'P'|=|BP'|\leq |BP|,\ \ \ |P'C'|=|PC|.\] W tym miejscu chciałbym sprostować stwierdzenie Redaktora Ligi z dorocznego omówienia (\(\Delta_{23}^{2}\)), jakoby nadesłane rozwiązania „ustępowały jednak prostotą rozwiązaniu, jakie znalazł autor zadania, i które zostało wydrukowane jako firmowe”. Powinno być: „rozwiązaniu, które wypracowali autor zadania i Redaktor Ligi” w trzech iteracjach: moje rozwiązanie (elementarne, ale nieco bolesne) zostało znacznie ulepszone przez Redaktora, a na koniec jeszcze raz przeze mnie uproszczone. Proponując zadanie, wyraziłem wprawdzie nadzieję, że w przyszłości przeczytam o ładniejszym podejściu, ale nie spodziewałem się, że w takich okolicznościach. Za tę zakulisową współpracę bardzo dziękuję!
Tutaj i dalej trójkąty i inne konfiguracje mogą być zdegenerowane, na przykład dopuszczamy \(A=B,\) chociaż w niektórych argumentach dla zwięzłości będziemy udawać, że nie są. Czytelnik z łatwością wypełni te luki, jest to tylko kwestia wypowiedzenia kilku dodatkowych słów, aby obsłużyć te proste przypadki.
Rys. 1
To tyle historii, teraz pora na Historię przez duże H, którą odkryłem dopiero jakiś czas później (i dobrze, bo obarczony tą wiedzą nie odważyłbym się zaproponować zadania). Zgodnie z regulaminem ligi ocenę maksymalną można otrzymać za podanie odsyłacza do literatury, „pod warunkiem, że w cytowanym źródle znajduje się pełne rozwiązanie”. W takim razie kilka osób mogłoby dostać punkt za odesłanie do swoich własnych prac, gdyby tylko Klub 44 miał nie 44, ale chociaż 99 lat. Jako pierwszy – polski matematyk Mojżesz Kirszbraun, którego praca magisterska na Uniwersytecie Warszawskim z 1930 roku, opublikowana w Fundamenta Mathematicae w roku 1934 [4], zawiera taki lemat:
To jedyna praca opublikowana przez Mojżesza Kirszbrauna (1903–1942), za to ma ona wg Google Scholar prawie 500 cytowań. Po studiach pracował jako aktuariusz; zmarł w getcie warszawskim w 1942 r.
Źródło: Biblioteka Instytutu Matematyki PAN, licencja CC-BY

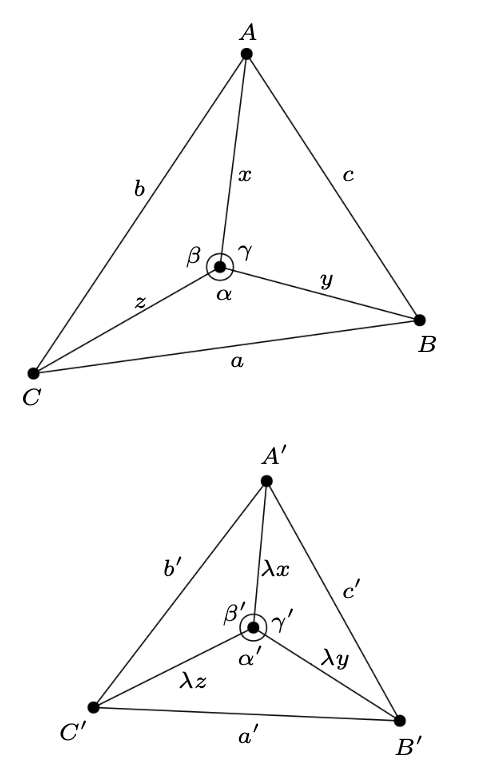
Jest to nic innego, jak zadanie \(842\) dla \(n+1\) kul \(n\)-wymiarowych w przestrzeni \(\mathbb{R}^n.\) Ten sam lemat odkrywali później inni autorzy (odnośniki w [5]), którzy tak jak Kirszbraun potrzebowali go, aby… ale o tym za chwilę. Punkty ligowe zebrałby nawet sam Michaił Gromow [3], który pokazał, że przecięcie kół po przesunięciu nie tylko jest niepuste, ale ma większą powierzchnię niż przed przesunięciem. Pierwszym, który poświęcił całą notkę wyłącznie naszemu zadaniu (dla dowolnej liczby kul w dowolnym wymiarze), był Isaac J. Schoenberg [5]. Jego krótki, analityczny dowód jest ekstraktem z prac poprzedników i w różnych wariantach występuje w późniejszych źródłach. Możemy prześledzić jego główną ideę dla naszego zadania. Żeby nie komplikować, ograniczymy się do sytuacji, gdy punkt \(P\) leży wewnątrz trójkąta \(ABC.\) Zamiast pracowicie szukać punktu \(P',\) weźmiemy od razu najlepszego możliwego kandydata i wykażemy, że jest on wystarczająco dobry. Zdefiniujmy więc \(P'\) jako punkt, który minimalizuje wartość wyrażenia \[\max\left(\frac{|P'A'|}{|PA|},\frac{|P'B'|}{|PB|},\frac{|P'C'|}{|PC|}\right),\] i niech to minimum wynosi \(\lambda.\) Chcemy pokazać, że \(\lambda\leq 1.\) Zauważmy, że \(P'\) leży w trójkącie \(A'B'C',\) bo w przeciwnym razie moglibyśmy przesunąć go w stronę tego trójkąta, zmniejszając jednocześnie wszystkie trzy odległości \(|P'A'|,|P'B'|,|P'C'|,\) co przeczy minimalności. Żeby znowu ułatwić sobie życie, rozpatrzymy tylko przypadek, gdy \(P'\) leży ściśle we wnętrzu trójkąta \(A'B'C'.\) Zauważmy, że wówczas \[\frac{|P'A'|}{|PA|}=\frac{|P'B'|}{|PB|}=\frac{|P'C'|}{|PC|}=\lambda,\] z przyczyn podobnych jak poprzednio: gdyby nie wszystkie trzy stosunki były równe, powiedzmy \(\lambda=\frac{|P'A'|}{|PA|}\geq\frac{|P'B'|}{|PB|}\geq\frac{|P'C'|}{|PC|}\) oraz \(\frac{|P'A'|}{|PA|}>\frac{|P'C'|}{|PC|},\) to przesuwając \(P'\) odrobinę w stronę boku \(A'B',\) moglibyśmy uzyskać lepsze minimum. Jesteśmy więc w sytuacji z rysunku 2. Przypuśćmy wbrew tezie, że \(\lambda > 1.\) Korzystając z twierdzenia cosinusów i pamiętając, że \(a'\leq a,\) dostajemy oszacowanie: \[\cos\alpha'=\frac{\lambda^2y^2+\lambda^2z^2-a'^2}{2\lambda^2yz}=\frac{y^2+z^2-\bigl(\frac{a'}{\lambda}\bigr)^2}{2yz}> \frac{y^2+z^2-a^2}{2yz}=\cos\alpha,\] więc \(\alpha'<\alpha.\) Ale analogicznie \(\beta'<\beta\) i \(\gamma'<\gamma\) – sprzeczność, więc jednak \(\lambda\leq 1.\) Schoenberg opowiada ten dowód w języku wektorów i iloczynu skalarnego w \(\mathbb{R}^n,\) co pozwala mu za jednym zamachem rozprawić się ze wszystkimi konfiguracjami, które pominęliśmy, ale esencja pozostaje ta sama.
Zagadnienie rosnącej objętości przecięcia i malejącej objętości sumy teoriomnogościowej zbliżających się kul to osobna puszka Pandory, której tutaj nie otwieramy. Hasło dla zainteresowanych: hipoteza Knesera–Poulsena.
Rys. 2
Podsumujmy i rozszerzmy to, co już wiemy. Teza zachodzi przy przesuwaniu \(n+1\) kul \(n\)-wymiarowych w \(\mathbb{R}^n.\) Jeden z podstawowych rezultatów w geometrii wypukłej, twierdzenie Helly’ego, głosi, że jeżeli mamy taką rodzinę zbiorów wypukłych w \(\mathbb{R}^n,\) że każde \(n+1\) zbiorów z tej rodziny ma niepuste przecięcie, to wszystkie zbiory mają niepuste przecięcie. Stąd wniosek, że nasza teza zachodzi dla dowolnie wielu (nawet nieskończenie wielu) kul. Co więcej, zestawy punktów \(A,B,C,P\ldots\) i \(A',B',C',P'\ldots\) z zadania 842(bis) mogą leżeć w różnych przestrzeniach, co pozostawiamy jako ćwiczenie. Reasumując to wszystko, dochodzimy do następującego uogólnienia.
Lemat. Niech \(\{A_i\}_{i\in I}\subseteq\mathbb{R}^N\) i \(\{A'_i\}_{i\in I}\subseteq\mathbb{R}^M\) będą dowolnymi zbiorami punktów indeksowanymi tym samym zbiorem indeksów \(I.\) Załóżmy, że dla dowolnych \(i,j\in I\) mamy \(|A'_iA'_j|\leq |A_iA_j|.\) Wtedy dla dowolnego punktu \(P\in\mathbb{R}^N\) istnieje taki punkt \(P'\in\mathbb{R}^M,\) że \(|P'A'_i|\leq |PA_i|\) dla wszystkich \(i\in I.\)
Możemy wreszcie zdradzić, do czego Kirszbraun i jego następcy używali tego lematu. Ważnym tematem w analizie i topologii jest zagadnienie przedłużania funkcji. Mając daną funkcję \(f:U\to V\) i większą dziedzinę \(U'\supseteq U,\) chcemy przedłużyć \(f\) z \(U\) na \(U',\) to znaczy znaleźć taką funkcję \(\widetilde{f}:U'\to V,\) że \(\widetilde{f}(X)= f(X)\) dla argumentów \(X\in U.\) Przedłużenie \(\widetilde{f}\) powinno zachowywać różne ładne własności funkcji \(f,\) którymi akurat jesteśmy zainteresowani. Klasyczny przykład: jeżeli \(\mathcal{A}\subseteq\mathbb{R}^N\) jest zbiorem domkniętym, to każdą funkcję ciągłą \(f:\mathcal{A}\to\mathbb{R}^M\) można przedłużyć do funkcji ciągłej \(\widetilde{f}:\mathbb{R}^N\to\mathbb{R}^M.\) Kirszbraun rozważał problem przedłużania dla funkcji lipschitzowskich. Funkcja \(f\) spełnia warunek Lipschitza ze stałą \(L,\) gdy \[|f(X)f(Y)|\leq L\cdot |XY|\] dla wszystkich argumentów \(X,Y,\) czyli gdy nie oddala punktów bardziej niż \(L\) razy. Pora wreszcie na następujące:
Twierdzenie o przedłużaniu funkcji lipschitzowskich (Kirszbraun). Niech \(f:\mathcal{A}\to\mathbb{R}^M\) będzie funkcją określoną na dowolnym podzbiorze \(\mathcal{A}\subseteq \mathbb{R}^N\) spełniającą warunek Lipschitza \(|f(X)f(Y)|\leq L\cdot |XY|\) dla wszystkich \(X,Y\in \mathcal{A}.\) Wtedy \(f\) można przedłużyć do funkcji \(\widetilde{f}:\mathbb{R}^N\to\mathbb{R}^M\) spełniającej warunek Lipschitza \(|\widetilde{f}(X)\widetilde{f}(Y)|\leq L\cdot |XY|\) dla wszystkich \(X,Y\in\mathbb{R}^N,\) z tą samą stałą \(L.\)
Dowód przeprowadzimy dla \(L=1,\) pozostawiając ogólną wersję jako zadanie. Następujące dwa zbiory punktów: \[\mathcal{A}\subseteq\mathbb{R}^N\ \ \ \ \ \ \mathrm{oraz}\ \ \ \ \ \ \mathcal{A}'=\{f(X)~:~X\in \mathcal{A}\}\subseteq\mathbb{R}^M\] indeksowane zbiorem \(\mathcal{A}\) spełniają założenia lematu. Weźmy teraz dowolny punkt \(P\in\mathbb{R}^N\setminus \mathcal{A}\) i zastosujmy do niego lemat, dostając na wyjściu punkt \(P'\in\mathbb{R}^M.\) Zdefiniujmy po prostu \(\widetilde{f}(P)=P'\) (oraz, oczywiście, \(\widetilde{f}(X)=f(X)\) dla \(X\in \mathcal{A}\)). Na mocy lematu funkcja \(\widetilde{f}\) spełnia warunek \(|\widetilde{f}(X)\widetilde{f}(Y)|\leq |XY|\) dla wszystkich \(X,Y\in \mathcal{A}\cup\{P\}.\)
Umiemy więc skonstruować odpowiednie przedłużenie funkcji \(f\) na dowolny nowy punkt \(P.\) A potem na następny i kolejny. Dowód można dokończyć na różne sposoby, zależnie od matematycznego wyrafinowania Czytelnika, na przykład z lematu Kuratowskiego–Zorna (bierzemy maksymalne przedłużenie; jego dziedziną musi być całe \(\mathbb{R}^N,\) bo inaczej moglibyśmy tą samą metodą rozszerzyć go o jeszcze jeden punkt, przecząc maksymalności) albo bardziej elementarnie, przedłużając przez indukcję na wszystkie punkty o współrzędnych wymiernych i następnie uciąglając w jedyny możliwy sposób.◻
Wnikliwy Czytelnik zauważy, że twierdzenie Kirszbrauna i poprzedzający go lemat to w zasadzie jedno i to samo: jeżeli przyjmiemy twierdzenie za prawdziwe, to lemat, a więc i rozwiązanie zadania 842, dostajemy za darmo (jak? to już ostatnie ćwiczenie!).
Na koniec pozwólmy, aby i Klub 44 dołożył swój mały kamyczek do tej Historii. W obszernej przeglądowej pracy o zastosowaniach twierdzenia Helly’ego [2] autorzy tak piszą, przez pryzmat twierdzenia Kirszbrauna, o \(n\)-wymiarowej wersji zadania 842: „Wszystkie dowody używają narzędzi analitycznych (iloczyn skalarny itp.), nawet w dwóch wymiarach, ale warto byłoby poszukać bardziej geometrycznego dowodu”. W dwóch wymiarach – zrobione!
Literatura
[1] Stephen Boyd and Lieven Vandenberghe. Additional exercises for Convex Optimization. https://github.com/cvxgrp/cvxbook_additional_exercises.
[2] Ludwig Danzer, Branko Grünbaum, and Victor Klee. Helly’s Theorem and its relatives. In Convexity: Proceedings of the Seventh Symposium in Pure Mathematics of the American Mathematical Society, volume 7, page 101. American Mathematical Soc., 1963.
[3] Mikhail Gromov. Monotonicity of the volume of intersection of balls. Geometrical Aspects of Functional Analysis, pages 1–4, 1987.
[4] Mojżesz D. Kirszbraun. Über die zusammenziehende und Lipschitzsche Transformationen. Fundamenta Mathematicae, 22(1):77–108, 1934.
[5] I. J. Schoenberg. On a Theorem of Kirzbraun and Valentine. The American Mathematical Monthly, 60(9):620–622, 1953.