Dany jest taki wielomian o współczynnikach rzeczywistych, że \(P(x)+P(-x)\) ma dokładnie 2025 różnych pierwiastków rzeczywistych. Znajdź wyraz wolny wielomianu \(P.\)
Liczbę naturalną nazwijmy dobrą, jeśli jest postaci \(n^{2}+1\) dla pewnej liczby całkowitej \(n.\) Udowodnić, że istnieje nieskończenie wiele liczb dobrych \(k,\) które nie posiadają dzielnika dobrego, różnego od 1 i \(k.\)
Załóżmy, że \(X\) jest zbiorem skończonym i niech \(X=\{x_{1}, x_{2}, \ldots, x_{k} \},\) gdzie \(x_{1}<x_{2}<\ldots <x_{k}.\) Zauważmy, że dowolna liczba ze zbioru \(Y\) posiada dzielnik ze zbioru \(X\) (jest nim np. najmniejszy dobry dzielnik liczby \(Y\)).
Rozpatrzmy liczbę \(A=(x_{1}x_{2}\ldots x_{k})^{2}+1.\) Ponieważ \(A\) jest liczbą dobrą większą niż \(x_{k},\) więc \(A\in Y.\) Wobec tego \(A\) posiada dzielnik w zbiorze \(X,\) co jest niemożliwe, gdyż \(x_{i}\mid A-1\) dla każdego \(i\in \{1,2,\ldots, k\}.\)
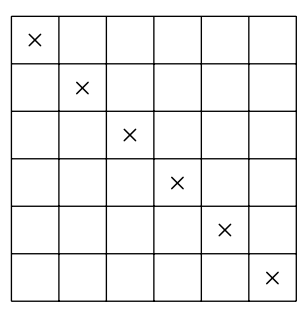
W tablicy \(n\times n\) \((n > 1)\) zaznaczono \(n+2\) kwadratów jednostkowych. Czy zawsze możemy tak przestawić wiersze i kolumny, aby wszystkie zaznaczone pola znajdowały się nad główną przekątną lub na niej? (Przyjmujemy, że kwadratowa tabela ma jedną główną przekątną, jak na rysunku).
Zaznaczmy \(4\) pola kwadratu \(2\times 2\) w lewym górnym rogu tablicy i zaznaczmy wszystkie pozostałe kwadraty na głównej przekątnej, jak na rysunku niżej.
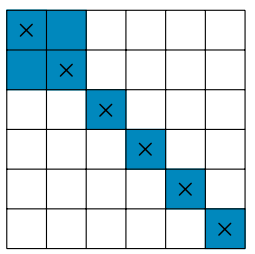
Pokażemy indukcyjnie, że nie możemy dokonać żądanego przestawienia wierszy i kolumn.
Dla \(n = 2\) jest to oczywiste (wszystkie pola kwadratu są zaznaczone). Załóżmy, że istnieje pożądane przegrupowanie wierszy i kolumn dla \(n > 2.\) Wybierzmy rząd zawierający tylko jeden zaznaczony kwadrat \(s.\) Wówczas kolumna zawierająca \(s\) nie zawiera innych zaznaczonych kwadratów. Jeżeli \(s\) nie znajduje się na głównej przekątnej, czyli znajduje się na prawo od niej, to kolumnę zawierającą \(s\) można przesunąć w lewo tak, aby \(s\) znalazł się na głównej przekątnej; wszystkie pozostałe kolumny albo pozostają na swoich miejscach, albo przesuwają się w prawo, więc warunek nie jest naruszony. Gdy \(s\) znajduje się już na głównej przekątnej, można go usunąć i zastosować założenie indukcyjne.
Pytanie: Co, jeśli zaznaczymy \(n+1\) kwadratów?
Początkiem astronomicznej wiosny jest dzień równonocy wiosennej, a astronomicznej jesieni – równonocy jesiennej. Są to dni, w których Słońce świeci prostopadle do osi ziemskiej. W tym roku (2025) wiosna rozpoczęła się 20 marca i także 20 marca rozpocznie się w roku przyszłym. Jesień rozpocznie się 22 września. Jak łatwo obliczyć, wiosna i lato potrwają łącznie 186 dni, a jesień i zima będą w sumie o tydzień krótsze i potrwają 179 dni. Skąd bierze się ta różnica?
Pełną ilościową analizę zagadnienia zawiera tekst: Jak wygląda orbita Ziemi?, \(\Delta^5_{84}\).
W dniach równonocy wiosennej (20 marca) i jesiennej (22 września), co łatwo sprawdzić w kalendarzu podającym godziny wschodu i zachodu Słońca, dzień trwa kilka minut dłużej niż następująca po nim noc, a rzeczywiste zrównanie czasu trwania dnia i nocy następuje około 3 dni przed dniem równonocy wiosennej i około 3 dni po równonocy jesiennej. Co jest przyczyną tego zjawiska?
Pełniejszą analizę można znaleźć w tekście: Kiedy zaczyna się jesień?, \(\Delta^8_{85}\).