Bartłomiej Pawlik
Matematyka lubi parkietaże. Do najprostszych należą te złożone z identycznych wielokątów foremnych. Pozwalają na to jedynie trójkąty równoboczne, kwadraty i sześciokąty foremne.

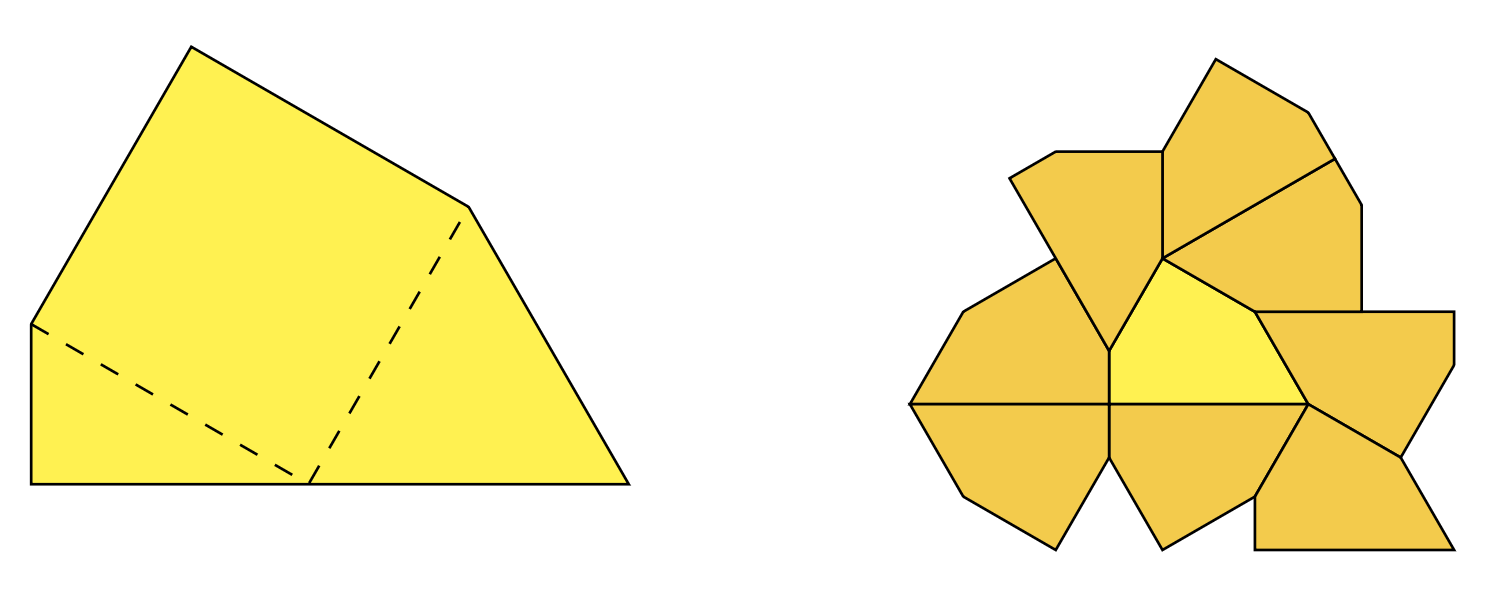
Do parkietaży interesujących matematycznie można zaliczyć te zbudowane za pomocą niedawno odkrytego „kapelusza Einsteina” (po lewej), a do interesujących estetycznie – te występujące w pracach M.C. Eschera (po prawej).

Co oczywiste, nie z każdej figury da się zrobić parkietaż. Rozluźnijmy zatem nasze wymaganie i zapytajmy o figury, których kopie mogą przynajmniej szczelnie otoczyć oryginalny egzemplarz. A jak to już się uda, to zastanówmy się, jak wiele warstw można w ten sposób utworzyć. Największy możliwy wynik będziemy nazywać liczbą Heescha danej figury.
Przyjmujemy, że liczba Heescha każdej figury tworzącej parkietaż płaszczyzny to \(\infty.\) Wskazanie figury o liczbie Heescha \(0\) nie jest zadaniem trudnym. Przedstawimy natomiast kilka takich, których liczba Heescha jest skończona i dodatnia.
W 1968 roku niemiecki matematyk Heinrich Heesch zaproponował prostą figurę, na którą można nałożyć dokładnie jedną warstwę: kwadrat z dołączonymi dwoma trójkątami – równobocznym oraz \(30^\circ\)–\(60^\circ\)–\(90^\circ\):
Odnotujmy, że krajan Heescha, Walther Lietzmann, 40 lat wcześniej przedstawił figurę na bazie koła, którą też da się otoczyć tylko jedną warstwą.
Jeżeli chcesz, Czytelniku Dociekliwy, odtworzyć rozwiązanie Lietzmanna, to wystarczy, że narysujesz fragment optymalnego upakowania identycznych kół na płaszczyźnie i spróbujesz tworzyć „łezki” poprzez łączenie każdego koła z jednym z przylegających do niego obszarów nienależących do żadnego koła. Szybko dojdziesz do wniosku, że parkietażu w ten sposób nie uzyskasz, a najlepsze, co możesz zrobić w tym kierunku, to otoczenie pojedynczej łezki jedną warstwą.
Ponad 20 lat po konstrukcji Heescha Anne Fontaine przedstawiła rodzinę figur, których liczba Heescha wynosi \(2.\) Niech \(a,b,c\) będą takimi liczbami całkowitymi, że \(0<a<b<c.\) Rozważmy następującą figurę o kształcie „spłaszczonej” litery \(\mathtt{U}\) (odcinki o wspólnym końcu są prostopadłe).
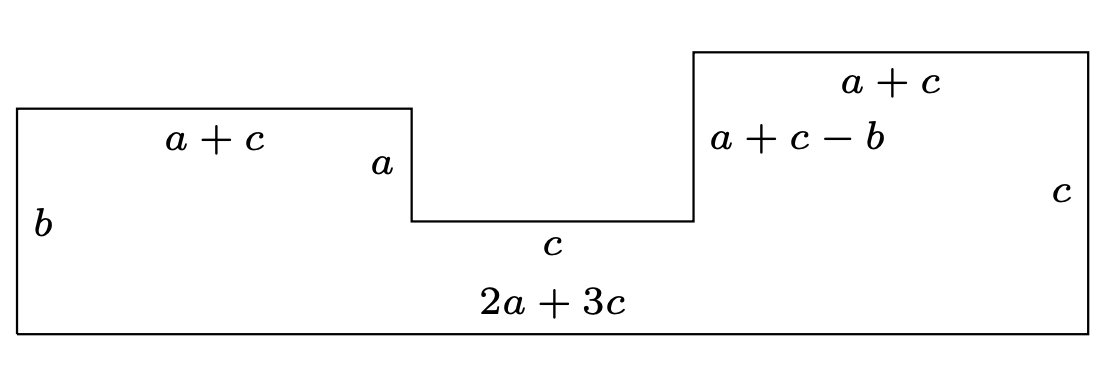
Poniższa ilustracja powinna przekonać Czytelnika, że liczba Heescha rozważanej figury faktycznie jest równa 2.
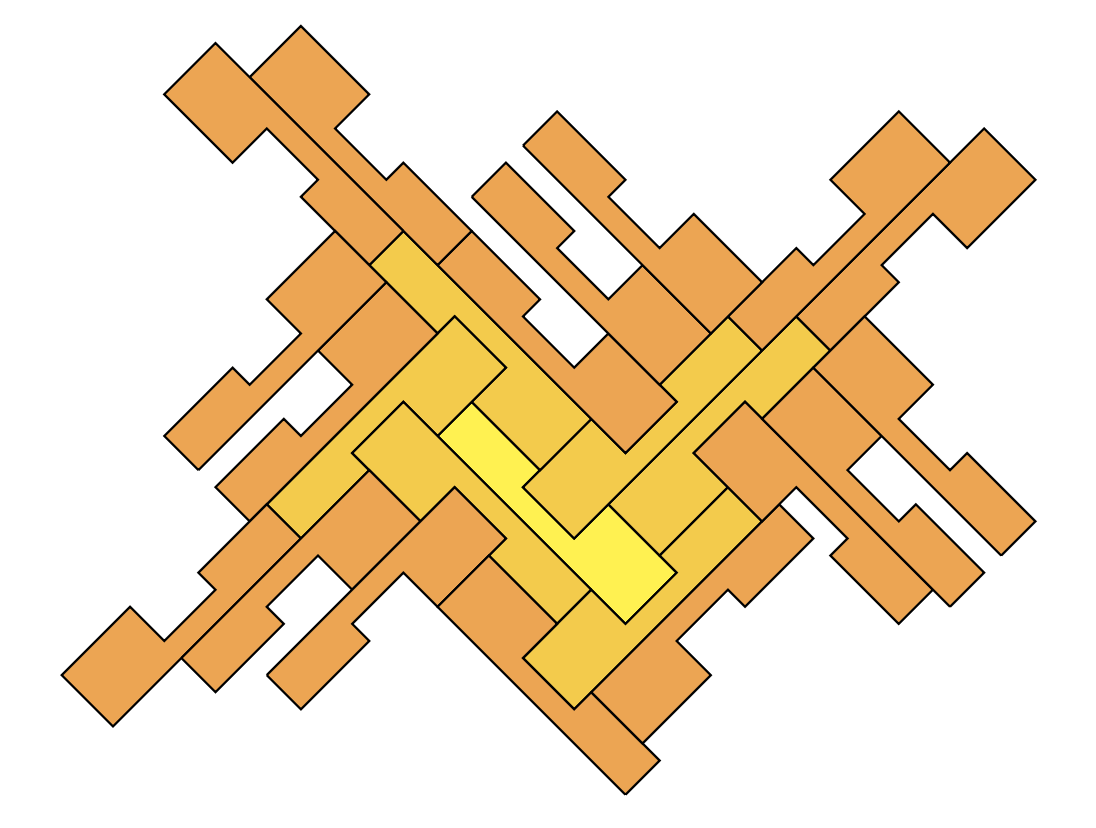
Warto zauważyć, że w przedstawionej reprezentacji graficznej druga warstwa pokrywa pierwszą w sposób nieoptymalny pod względem liczby użytych figur.
W ciągu ostatnich trzydziestu lat pojawiały się kolejne konstrukcje figur z liczbami Heescha równymi \(3,\) \(4\) i \(5.\) Najnowszym wynikiem jest zaprezentowana w 2020 roku figura o liczbie Heescha 6, której odkrywcą jest Bojan Bas̆ić.
Obecnie nie znamy żadnej figury o liczbie Heescha równej 7. Nie wiadomo też, czy dla każdej liczby naturalnej \(k\) istnieje figura o liczbie Heescha równej \(k\) – to zagadnienie znane jest jako problem Heescha.
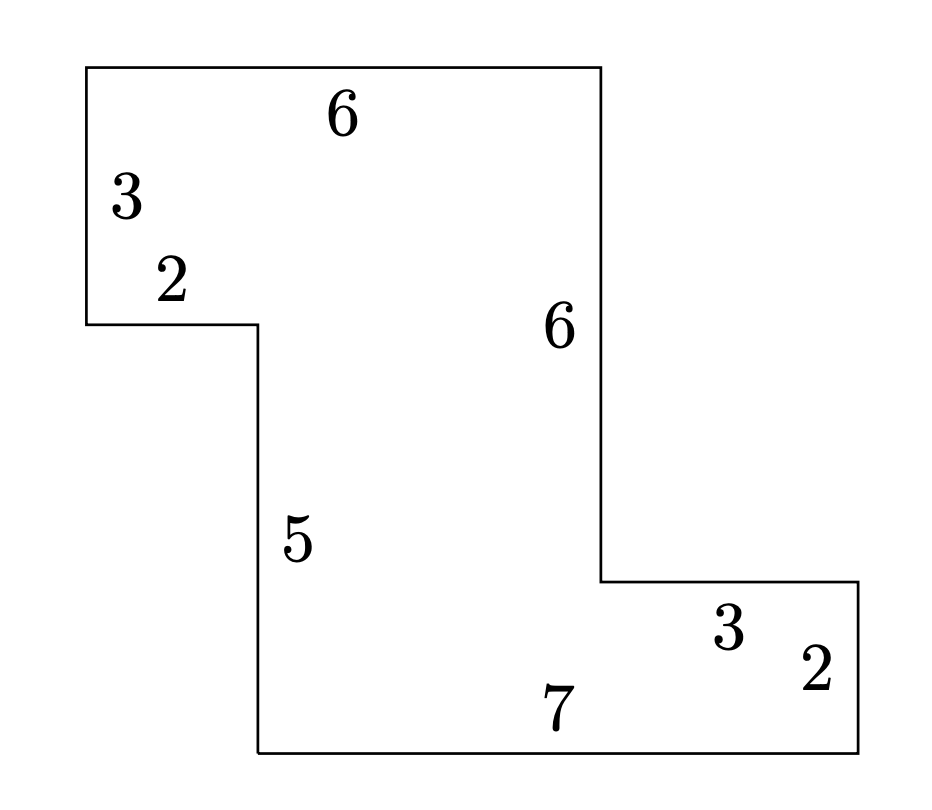
Na koniec wróćmy do artykułu Anne Fontaine. Autorka stwierdziła w nim, że zna też inne figury o liczbie Heescha 2, w tym poniższą figurę w kształcie litery \(\mathtt{Z}.\) Czy potrafisz, Czytelniku, zbudować obie warstwy na tej figurze?