Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Plotkare humanum est. Każdy z nas lubi być dystrybutorem plotek, choć niekoniecznie ich obiektem. W artykule Plotki, ploteczki, plotunie… z \(\Delta^{12}_{22}\) zastanawialiśmy się, jak szybko mogą roznosić się plotki w grafach. Przypomnijmy rozważany tam model: w pewnym mieście znajduje się \(n\) plotkarzy, z których każdy zna każdego. Podczas rozmowy telefonicznej dwóch plotkarzy wymienia się wszystkimi posiadanymi informacjami. Na początku dnia każdy z plotkarzy jest w posiadaniu pewnej informacji, której nie ma żaden z pozostałych. Jaka jest najmniejsza liczba rozmów telefonicznych, które należy przeprowadzić, aby wszyscy wszystko wiedzieli?
Dla przykładu, przy czterech plotkujących \(A,\) \(B,\) \(C,\) \(D\) wystarczą cztery połączenia: najpierw \(A\) rozmawia z \(B,\) potem \(C\) rozmawia z \(D,\) następnie \(A\) rozmawia z \(D\) (dzięki czemu obaj wiedzą wszystko o wszystkich) i na koniec \(B\) rozmawia z \(C\) (przez co oni również stają się wszechwiedzący). Można nietrudną analizą uzasadnić, że w tym wypadku trzy połączenia to za mało.
W przytoczonym artykule pada odpowiedź: \({2n-4}\), wraz z bardzo chytrym uzasadnieniem. W niniejszym tekście zastanowimy się, co by było, gdyby fabuła zadania rozgrywała się 300 lat wcześniej, w czasach gdy jedyną formą plotkowania na odległość było pisanie listów.
Na początek pewna rozsądnie brzmiąca intuicja: w kontekście wymieniania się plotkami jedna rozmowa telefoniczna jest równoważna wysyłce dwóch listów. Skoro współcześnie potrzebujemy \(2n-4\) połączeń telefonicznych do zrealizowania plotkarskich zamierzeń, to można by oczekiwać, że w czasach przedtelefonowych wymagana liczba listów to około dwukrotność tej liczby, czyli \(4n-4\) („około” bierze się z dopuszczenia drobnych subtelności, mogących zmienić wynik o stałą).
Czytelnik Podejrzliwy przeczuwa zapewne, że przedstawienie na początku artykułu „rozsądnie brzmiącej intuicji” zwiastuje jej rychłe obalenie – i tak też jest w tym przypadku. Wystarczy bowiem \({2n-2}\) listów, czyli tylko o dwa więcej niż połączeń telefonicznych! Uzasadnimy najpierw, dlaczego tyle wystarczy. Ustawmy naszych plotkarzy w ciąg \(P_1,\ldots,P_n\) i niech \(i\)-tym wysłanym listem będzie \(P_i\to P_{i+1}\) dla \(i\leq n-1\) oraz \(P_{2n-i}\to P_{2n-i-1}\) dla \(n\leq i\leq 2n-2.\) Innymi słowy, puszczamy najpierw „łańcuszek” od \(P_1\) do \(P_n,\) tak by \(P_n\) stał się wszechwiedzący, a potem pozwalamy \(P_n\) odesłać tę wiedzę pozostałym, aż do \(P_1.\)
Intensywność strzałki odpowiada kolejności, w jakiej plotkarze powinni wysłać listy, żeby wszyscy dowiedzieli się wszystkiego o wszystkich
Pokażemy teraz, że mniejsza liczba listów nie wchodzi w grę. Zauważmy najpierw, że po \(n-2\) wysłanych listach żaden z plotkarzy nie wie wszystkiego o wszystkich. Rzeczywiście, aby taki plotkarz zaistniał, każdy z pozostałych \(n-1\) plotkarzy musiał rozstać się ze swoją tajemnicą, a to następuje wyłącznie na skutek wysłania do kogoś listu. Począwszy od \((n-2)\)-go listu, każdy kolejny zwiększa liczbę „wszechwiedzących” plotkarzy o co najwyżej 1, gdyż tylko odbiorca wiadomości powiększa w wyniku jej wysłania swoją wiedzę (w przypadku telefonicznym jest inaczej, co utrudnia jego analizę). Ponieważ dążymy do uzyskania \(n\) wszechwiedzących plotkarzy, musi być wysłanych jeszcze co najmniej \(n\) listów, co daje szukane ograniczenie \(2n-2.\)
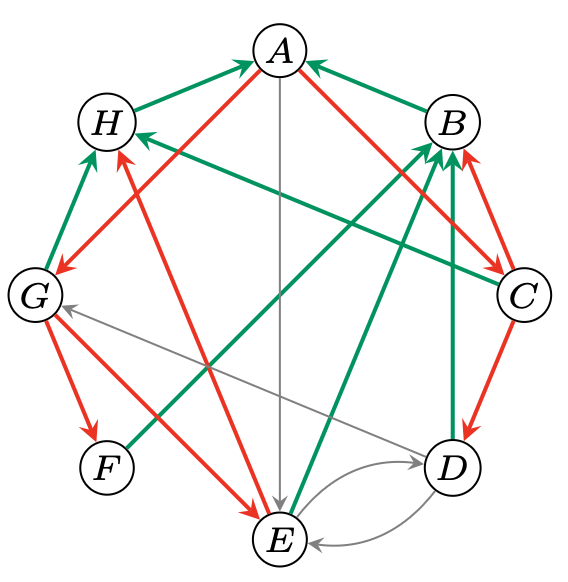
Tak mógłby wyglądać graf skierowany możliwych połączeń między ośmioma plotkarzami. Na zielono zaznaczono połączenia odpowiadające 7 listom, dzięki którym \(A\) dowiaduje się wszystkiego od pozostałych, zaś na czerwono – 7 listów, za pośrednictwem których pozostali plotkarze dowiadują się następnie wszystkiego od \(A.\) Zielone i czerwone krawędzie nie muszą być rozłączne, jednak zostały tak wybrane dla czytelności
Zastanówmy się jeszcze, czy odpowiedź na nasze pytanie uległaby zmianie, gdyby każdy z plotkarzy miał „czarną listę” innych plotkarzy, do których na pewno nigdy nie wyśle korespondencji (bo na przykład kiedyś rozpuszczali o nim kłamliwe plotki). Wyobraźmy sobie graf, którego wierzchołkami są plotkarze, zaś strzałka od plotkarza \(A\) do \(B\) oznacza, że ten pierwszy dopuszcza wysłanie listu do tego drugiego. Żeby w opisanej sytuacji pełna wymiana informacji była w ogóle możliwa, przedstawiony graf musi być silnie spójny – z każdego wierzchołka możemy dojść do dowolnego innego, poruszając się po strzałkach. Załóżmy zatem, że tak jest, i wybierzmy dowolnego plotkarza \(A.\) Z założenia o silnej spójności wynika, że z wszystkich plotkarzy i wybranych połączeń między nimi możemy utworzyć „drzewo skierowane w górę”, do znajdującego się na szczycie \(A.\) W takim grafowym drzewie o \(n\) wierzchołkach mamy zawsze \(n-1\) krawędzi, zatem tyle listów wystarczy, aby \(A\) dowiedział się wszystkiego o wszystkich (listy wysyłane są w kolejności wyznaczonej przez „drzewową” odległość od \(A\)). Możemy też utworzyć inne drzewo z \(A\) na szczycie, w którym wszystkie krawędzie będą skierowane „w dół”. To drzewo pozwoli \(A\) rozdystrybuować swoją wszechwiedzę wśród pozostałych plotkarzy za pomocą kolejnych \(n-1\) listów. Wniosek: jeśli tylko plotkarze mogą w pełni wymienić się informacjami, wystarczy im do tego celu \(2n-2\) wysłanych listów. Niezależnie od tego, kto, z kim, dlaczego, na co, po co i w jakim celu.