Delta 10/2025

Zadania

Dominik Burek i Andrzej Majhofer

image

image

Zadanie M 1831

Na tablicy zapisana jest cyfra \(7.\) Wanda i Staś na zmianę dodają jedną cyfrę do aktualnej liczby na tablicy, zaczyna Wanda. Cyfrę można dodać na początku liczby (z wyjątkiem zera), na jej końcu lub pomiędzy dowolnymi dwiema cyframi. Zwycięzcą zostaje ta osoba, po ruchu której liczba na planszy jest kwadratem liczby całkowitej. Udowodnić, że żaden z graczy nie może być pewien wygranej.

Rozwiązanie
W pierwszym ruchu Wanda nie przegra, ponieważ nie ma dwucyfrowych kwadratów liczb całkowitych z cyfrą 7. Pokażemy teraz, że każdy z graczy może mieć pewność, że nie przegra, wybierając jedną z cyfr 7 lub 8 i dodając ją na końcu bieżącej liczby w grze.

Istotnie, kwadrat liczby całkowitej nie może kończyć się cyfrą 7 ani 8, więc przy tej strategii przeciwnik może wygrać jedynie poprzez dodanie nowej cyfry na końcu liczby. Załóżmy, że po dopisaniu cyfry 7 do aktualnej liczby \(A\) istnieje zwycięska odpowiedź – dopisanie cyfry \(x,\) a poprzez dopisanie cyfry 8 istnieje zwycięska odpowiedź – przypisanie cyfry \(y.\) W tym przypadku liczby \(\overline{A7x}\) i \(\overline{A8y}\) byłyby kwadratami liczb całkowitych. Różnica między nimi wyniosłaby mniej niż \(20,\) ale każda z tych liczb jest co najmniej trzycyfrowa i różnica między sąsiednimi kwadratami takich liczb całkowitych wynosi co najmniej \(11^2-10^2>20.\)

Zadanie M 1832

Niech \(n \geq 3\) będzie liczbą całkowitą. Udowodnić, że dla dowolnej liczby całkowitej \(1 \leq k \leq \binom{n}{2}\) istnieje zbiór \(\mathcal{A}\) składający się z \(n\) takich liczb całkowitych dodatnich, że zbiór \[\{\textup{NWD}(x, y)\colon x, y \in \mathcal{A},\; x \neq y \}\] zawiera dokładnie \(k\) różnych elementów.

Rozwiązanie
Rozpatrzmy dowolny graf \(\mathcal{G}\) o \(k-1\) krawędziach oraz \(n\) wierzchołkach ponumerowanych kolejno \(1, 2, \ldots, n,\) i mający \(k-1\) krawędzi. Niech \(p_{n}\) oznacza \(n\)-tą liczbę pierwszą. Każdej krawędzi \(\mathcal{G}\) przypiszmy pewną liczbę pierwszą ze zbioru \(\{p_1, p_{2}, \ldots, p_{k-1}\}.\) Natomiast wierzchołkowi o numerze \(i\) przypiszmy iloczyn liczb pierwszych odpowiadających krawędziom wychodzącym z tego wierzchołka oraz liczby \(p_{k+i}.\)

Liczby przypisane wierzchołkom są parami różne, gdyż wierzchołek o numerze \(i\) ma przypisaną liczbę, która jako jedyna jest podzielna przez \(p_{k+i}.\) Ponadto zbiór największych wspólnych dzielników par tych \(n\) liczb składa się dokładnie z liczb \(p_1,\) \(p_2,\) \(\ldots,\) \(p_{k-1}\) oraz \(1.\) Wobec tego zbiór \(\mathcal{A}\) wszystkich liczb przypisanych wierzchołkom \(\mathcal{G}\) spełnia warunki zadania.

Zadanie M 1833

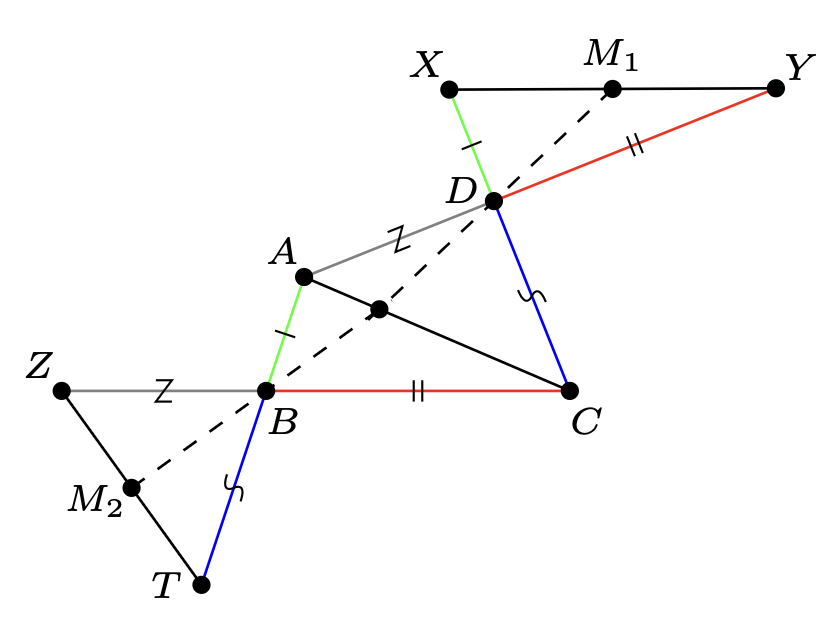
Niech \(ABCD\) będzie czworokątem wypukłym. Punkty \(X\) i \(Y\) leżą na przedłużeniach boków, odpowiednio, \(CD\) i \(AD\) (przedłużamy od strony punktu \(D\)) w taki sposób, że \(DX = AB\) i \(DY = BC.\) Podobnie punkty \(Z\) i \(T\) leżą na przedłużeniach boków, odpowiednio, \(CB\) i \(AB\) (od strony \(B\)) w taki sposób, że \(BZ = AD\) i \(BT = DC.\) Niech \(M_1\) będzie środkiem \(XY,\) a \(M_2\) środkiem \(ZT.\) Udowodnić, że proste \(DM_1, BM_2\) i \(AC\) przecinają się w jednym punkcie.

Rozwiązanie
W rozwiązaniu użyjemy dobrze znanej (i bardzo przydatnej!) konsekwencji twierdzenia sinusów w trójkącie (zob. też KPO z numeru \(\Delta^{10}_{25}\)):

W trójkącie \(ABC\) punkt \(D\) leży na odcinku \(BC.\) Wówczas \[\frac{BD}{DC}=\frac{\sin \measuredangle BAD}{\sin \measuredangle DAC}\cdot \frac{BA}{AC}.\]

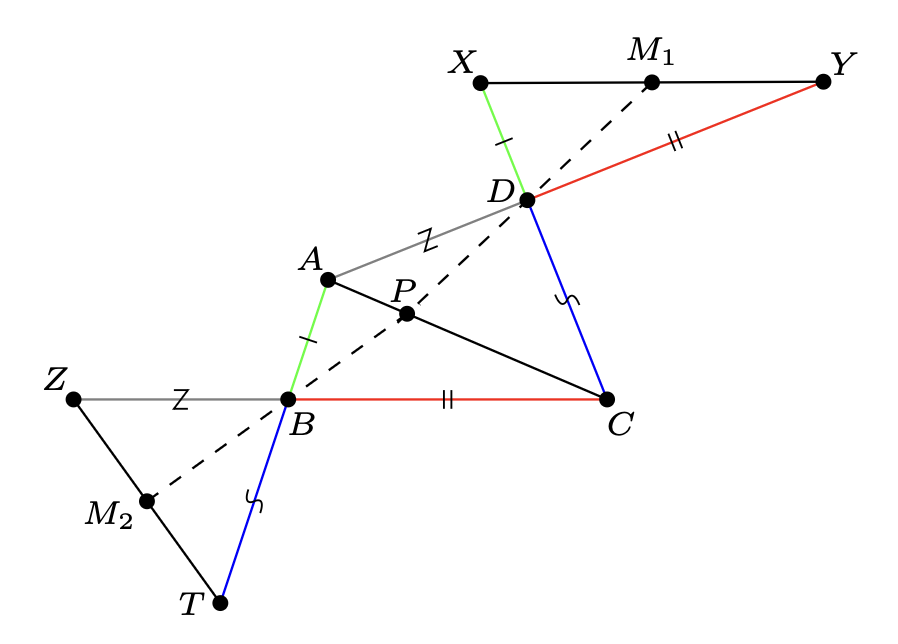
Niech \(DM_1\) przecina \(AC\) w punkcie \(P.\) Wówczas \[\begin{aligned} \frac{AP}{PC} & =\frac{\sin \measuredangle ADP}{\sin \measuredangle PDC}\cdot \frac{AD}{DC}=\frac{\sin \measuredangle YDM_1}{\sin \measuredangle M_1DX}\cdot \frac{AD}{DC} \\&=\frac{YM_1}{M_1X}\cdot \frac{XD}{DY}\cdot \frac{AD}{DC}=\frac{XD}{DY}\cdot \frac{AD}{DC}. \end{aligned}\]

Podobnie, jeśli \(BM_2\) przecina \(AC\) w punkcie \(P',\) uzyskamy \[\frac{AP'}{P'C}=\frac{ZB}{BT}\cdot \frac{AB}{BC}.\] Jednakże na podstawie danych w zadaniu zależności prawe strony ostatnich dwóch równości mają tę samą wartość, więc \(P=P'.\)

image

Zadanie F 1129

W najniższej warstwie atmosfery (w troposferze) temperatura powietrza jednostajnie maleje z wysokością, po czym (w stratosferze) zaczyna rosnąć wraz ze wzrostem wysokości nad powierzchnią Ziemi. Wysokość tropopauzy – granicy między troposferą i stratosferą – zależy od szerokości geograficznej i zmienia się od około 18 km nad równikiem do około 6 km nad biegunami (średnia to ok. 13 km). Natężenie dźwięku samolotu lecącego w obszarze tropopauzy, w warstwie powietrza o grubości rzędu 1 km, maleje z odległością \(R\) od źródła jak \(1/R.\) Z czego wynika taka zależność?

Rozwiązanie
Prędkość \(c\) dźwięku w gazie o temperaturze bezwzględnej \(T,\) molowej masie \(\mu\) i wykładniku adiabaty \(\kappa\) wynosi: \[c = \sqrt{\frac{\kappa RT}{\mu}}\] (\(R\) jest stałą gazową). Wraz z oddalaniem się od tropopauzy w górę lub w dół temperatura powietrza rośnie, a więc rośnie też prędkość dźwięku. Oznacza to, że fale dźwiękowe wzbudzone w tropopauzie są załamywane zawsze w stronę tropopauzy, a więc dźwięk efektywnie rozprzestrzenia się w dwuwymiarowym obszarze tropopauzy, co prowadzi do malenia jego natężenia z odległością od źródła jak \(1/R.\)
Zadanie F 1130

Stacja kosmiczna ma kształt walca o promieniu \(r_0.\) W dążeniu do stworzenia astronautom warunków możliwie zbliżonych do warunków na Ziemi stację wypełniono powietrzem i nadano jej ruch obrotowy z prędkością kątową \(\omega\) dobraną tak, żeby na brzegu walca przyspieszenie było równe przyspieszeniu ziemskiemu, \(g.\) Jaki jest stosunek \(p_0\) ciśnienia powietrza na brzegu stacji do ciśnienia \(p_c\) w jej centrum (tj. na osi walca)? Średnia molowa masa powietrza wynosi \(\mu,\) a wewnątrz stacji temperatura jest stała i w skali Kelvina wynosi \(T.\)

Rozwiązanie
Obracająca się stacja jest układem nieinercjalnym. W jej wnętrzu przyspieszenie odśrodkowe \(a(r)\) zmienia się z odległością \(r\) od osi walca: \(a(r) = \omega^2 r.\) Na brzegu walca \(a(r_0) = \omega^2 r_0 = g,\) czyli: \[a(r) = \frac{gr}{r_0}.\] Po ustaleniu równowagi powietrze obraca się wraz z całą stacją, a przyspieszenie \(a(r)\) odgrywa rolę pola grawitacyjnego. Znajdziemy rozkład ciśnienia \(p(r)\) w polu \(a(r).\) Niech \(\rho(r)\) oznacza gęstość powietrza w odległości \(r\) od osi obrotu. Mamy: \[\frac{dp}{dr} = a(r)\rho(r).\] Powietrze spełnia równanie gazu doskonałego, a więc: \[\rho(r) = \frac{p(r)\mu}{RT}.\] \(R\) oznacza tu stałą gazową. Otrzymujemy równanie: \[\frac{dp}{dr} = \left(\frac{\mu gr}{r_0RT}\right)p,\] którego rozwiązaniem jest (\(p_c = p(0)\)): \[p(r) = p_c\exp\left(\frac{\mu gr^2}{2r_0RT}\right).\] Szukany stosunek ciśnień wynosi więc: \[\frac{p_c}{p_0} = \exp\left(-\frac{\mu gr_0}{2RT}\right).\]