Matematyka i literatura: OuLiPo

Afiliacja: Instytut Matematyki Stosowanej i Mechaniki, Uniwersytet Warszawski

Czy ma sens szukanie związków matematyki z literaturą? Czy to, co znajdziemy, nie będzie zbyt naciągane i powierzchowne? Już sam fakt, że zadanie to nie wydaje się łatwe, powinien jednak zachęcić wiele osób poszukujących, w tym związanych z matematyką, do jego zgłębienia. Wszak, jak coś trudne, to wartościowe: trudność jest największą wartością, przynajmniej w matematyce. Czy nauka nie polega właśnie na łączeniu odległych bytów? Wymieńmy na przykład takie czasopisma, jak Journal

of Mathematics and the Arts oraz Journal of Humanistic Mathematics, w których regularnie pojawiają się artykuły tropiące takie związki. Matematyka i literatura są zbyt stare, by nie było okresu, kiedy to „miały się ku sobie”.

Bardzo lubię następującą metaforę. Matematyka i literatura są jak dwie strony tej samej monety. Nigdy się nie spotkają, ale razem tworzą całość. Matematyka i literatura przetwarzają rzeczywistość, są wynikiem naszego doświadczenia i obserwacji świata. Są czystymi produktami naszych umysłów.

W tym artykule przedstawię francuską grupę literacką OuLiPo. Czytelników Zainteresowanych dodatkowymi informacjami odsyłam do pracy Davida Bellosa oraz bibliografii w niej zamieszczonej. OuLiPo powstało w Paryżu w latach 60. ubiegłego stulecia. Jednym z celów działania grupy było opracowanie zasad matematycznych w literaturze. Próbowano opierać literaturę na wzorcach matematycznych, szczególnie inspirując się kombinatoryką, logiką, ale też regułami szachowymi.

D. Bellos, Mathematics, poetry, fiction: the adventure of the OuLiPo, BSHM Bulletin, vol. 25, 2010, 104–118.

Za twórców grupy uchodzą pisarz Raymond Queneau (1903–1976) oraz François Le Lionnais (1901–1984), inżynier, matematyk i pisarz. Obok przykład prowokacji literackiej Le Lionnais’a – utwór Wiersz w stanie śladowym – zdecydowanie lepiej wychodzi, gdy się go deklamuje i jednocześnie interpretuje, zwracając uwagę na interpunkcję. Bardziej znanym w świecie literatury jest zapewne Queneau. Ma nawet „swoją” stację metra w Paryżu.

Wiersz w stanie śladowym
1, 2, 3, 4, 5,
6, 7, 8, 9, 10,
12?
11!

Nazwa „OuLiPo” pochodzi od Ouvroir de Literature Potentielle, czyli Warsztaty Literatury Potencjalnej. Grupa działała długo i jest, być może, jedną z najdłużej działających grup literackich. Trudno się dziwić, skoro zasady organizacyjne głoszą, że członkiem zostaje się na wieczność. Zebrania grupy gromadziły licznych widzów, zachwyconych prowadzonymi dyskusjami. Do grupy należeli także George Perec (1936–1982) oraz Italo Calvino (1923–1985), ten ostatni jako członek honorowy. Pełną listę wiecznych członków OuLiPo można znaleźć w Internecie lub w wymienionej wcześniej pracy. Warto tu zwrócić uwagę, że rodzina George’a Pereca pochodziła z Polski (znajdująca się w Warszawie ulica Pereca wzięła jednak swoją nazwę od Icchoka Pereca, również pisarza).

Queneau zainteresował się utworem zwanym sekstyną liryczną, zapewne wymyśloną przez XIII–wiecznego trubadura Arnaut Daniela. Sekstyny pisali m. in. Dante, Petrarka i Barańczak. Jest to utwór o specyficznej strukturze, składający się z 6 strof 6-wersowych i końcowej strofy 3–wersowej. Ostatnie wyrazy w wersach każdej strofy są różne. Powtarzają się jednak między strofami, za każdym razem w innym porządku. Zmiana kolejności w stosunku do poprzedniej strofy odbywa się według tego samego, „spiralnego”, sposobu, na przykład zamieszczonego obok. Postępując według tego schematu, otrzymamy następującą strukturę (w kolumnach przedstawiona jest kolejność ostatnich wyrazów w poszczególnych strofach): 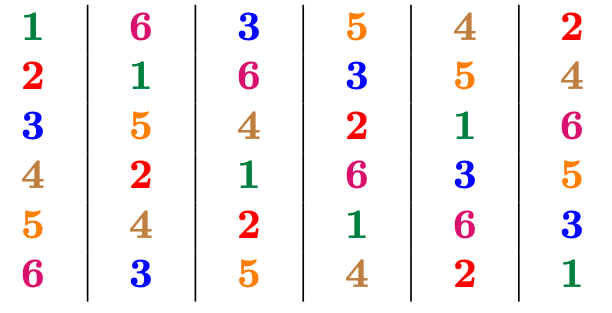Gdybyśmy dokonali kolejnego kroku, wrócilibyśmy do układu w pierwszej strofie. Otrzymaliśmy zatem strukturę okresową o okresie \(6,\) przy czym każdy wyraz końcowy był za każdym razem w wersie o innym numerze. Queneau zadał sobie pytanie, czy taki spiralny schemat wciąż ma przedstawioną własność, jeżeli \(6\) zamienić na inną liczbę naturalną \(n\)? Jeśli tak, liczbę \(n\) nazywamy dopuszczalną lub liczbą Queneau, zaś samą wynikającą strukturę: \(n\)-iną lub \(n\)-queniną. Rozważmy dla przykładu \(n=4.\) Spiralny sposób mieszania daje nam kolejność 4, 1, 3, 2. Ostatni wyraz z 3 wersu pozostał na swoim miejscu, a zatem 4 nie jest liczbą dopuszczalną.

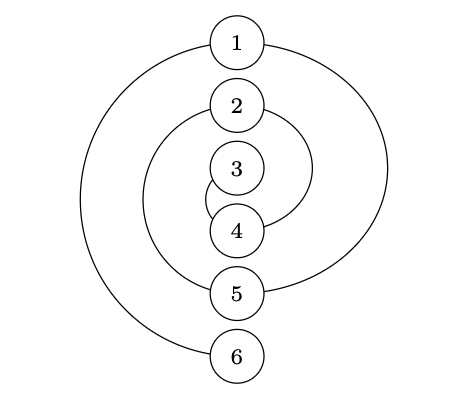
Idąc wzdłuż spirali, zaczynając od dołu, odczytujemy kolejne wiersze, z których mamy zaczerpnąć kończące słowa: 6, 1, 5, 2, 4, 3.

M.P. Saclolo, How a Medieval Troubadour Became a Mathematical Figure, 2011, Notices of the American Mathematical Society, 2011, 58(5); correction–addition in Letters to the Editor, Notices of the American Mathematical Society, 2011, 58(7).

Sam Queneau (literat, ale też członek Francuskiego Towarzystwa Matematycznego!) udowodnił, że liczby postaci \(\, n \, =\, 2jk+j+k\„\) dla liczb naturalnych \(j\) i \(k,\) nie są dopuszczalne, np. \(4,\) \(7,\) \(10,\) 12 nie są, oraz znalazł wszystkich \(31\) liczb nie większych od \(100,\) które są dopuszczalne, np. \(69.\) Badania nad tymi liczbami były przeprowadzone w kilku zaawansowanych matematycznie pracach. Odnośniki można znaleźć w bibliografii do pracy M.P. Saclolo (patrz margines). Zagadnienie to stało się źródłem inspiracji do rozwoju interesujących idei matematycznych. Zatem literatura odegrała tu podobną rolę, jaką w historii niejednokrotnie odgrywała fizyka, dając impuls do badań matematycznych. Interesującym pytaniem jest, czy A. Daniel mógł w XIII wieku zdawać sobie sprawę z wewnętrznego bogactwa jego sekstyny? Podobne wrażenie intuicji wychodzącej ponad możliwą wiedzę odnajdujemy u Dantego.

M. Lachowicz, Intuicja matematyczna w Raju?, \(\Delta^9_{21}\).

Bardzo znanym dziełem Queneau jest utwór Sto tysięcy miliardów wierszy. Jest to zbiór 10 sonetów. Każdy sonet składa się z 14 wersów, w taki sposób, że kolejne wersy są ze sobą wymienialne. Jeżeli ponumerujemy wszystkie wersy od \(1\) do \(14,\) to następnie możemy wymienić każdy wers \(k\) z każdym innym (tzn. z innego sonetu) wersem \(k\) bez utracenia rymów i sensu (poetyckiego) całości. W rezultacie możemy sobie złożyć „własny” sonet, mając 10 możliwości do utworzenia każdego wersu. Ponieważ wersów jest \(14,\) więc mamy \(10^{14}\) możliwości i tyleż różnych możliwych sonetów. Liczba \(10^{14}\) to właśnie sto tysięcy miliardów, \(10^{14} = 10^2 \times 10^3 \times 10^9.\) Czas potrzebny na przeczytanie wszystkich możliwych sonetów Queneau to około 200 milionów lat bezustannego czytania, a zatem z punktu widzenia życia ludzkiego jest porównywalny z nieskończonością. W ten sposób autor stworzył dzieło, którego sam w pełni nie mógł kontrolować. Może to przyczynek do dyskusji o sztucznej inteligencji?

R. Queneau, Sto tysięcy miliardów wierszy, Halart 2008. Zdjęcie: Thomas Guest, CC BY 2.0, via Wikimedia Commons

Edward Stachura, Się, 1977, str. 171.

Na mniejszą skalę zasady kombinatoryki stosował Edward Stachura w powieści Się. Zdanie (jakże mi bliskie) „Się szło powolutku skrajem drogi straszliwie i cudownie samotnym” pojawia się \(22\) razy z przestawionymi (spermutowanymi) wyrazami, w taki sposób, że tworzy całość poetycką. Oczywiście wszystkich możliwych permutacji jest dużo więcej niż 22, ale sens poetycki miał wartość nadrzędną.

R. Queneau, Ćwiczenia stylistyczne, Czuły Barbarzyńca, 2005.

Dorota Kassjanowicz, 30 znikających trampolin, Albus, 2016; II wydanie, 2022.

W Ćwiczeniach stylistycznych Queneau opowiada banalną historyjkę o mężczyźnie w autobusie paryskim na \(99\) sposobów, od „ścisłego”, „filozoficznego”, „trzynastozgłoskowego” po „obraźliwy”. Wielokrotnie spotkałem opinię, że jest to jedna z najśmieszniejszych książek. Napisana zgodnie z zasadą OuLiPo, wedle której nic tak nie sprzyja literaturze jak ograniczenia formalne. Czyżby znowu to było wyabstrahowanie naszego odczucia świata? W podobny sposób konstruuje swoją książkę dla dzieci Dorota Kassjanowicz. Jest to historia znikającej ogrodowej trampoliny opowiedziana na \(30\) sposobów, pełna zabawy słowami i odniesień do różnych konwencji. Książka, która może być źródłem zabawy zarówno dla dzieci, jak i dorosłych, w domu, na lekcjach polskiego czy na zajęciach teatralnych. Gorąco polecam każdej wrażliwej osobie, lubiącej językowe niespodzianki i wyzwania!

George Perec, Zniknięcia, Lokator, 2022.

Oto fragment znanego utworu z polskiego tłumaczenia Zniknięcia:
Litwo! Ojczyzno moja! Tyś jak zdrowia okaz,
Ów tylko cię dozgonną miłością pokocha,
Kto cię stracił. Dziś urok twój całą osobą
Widzę i opisuję, bo tęsknię za tobą.
...
Nie pojawia się tu litera „e”, natomiast pojawia się litera „ę”. Wyjaśnienie znajdzie Czytelnik w posłowiu książki.

Twórczość Georga Pereca jest bardzo trudna do skrótowego przedstawienia. Niedawno ukazały się tłumaczenia na język polski dwóch jego książek, które chciałbym przybliżyć Czytelnikom Delty. Pierwszą jest La Disparition, czyli Zniknięcia. Po jej ukazaniu się w roku 1969 we Francji niektórzy krytycy byli pełni uznania za swoisty, nowatorski język. Zapewne nie wszyscy zauważyli, że to, co w książce znika, to litera „e”, która, wraz z wersjami akcentowanymi, jest najczęściej występującą literą w języku francuskim (ok. \(14\%\)). Dla porównania, w języku polskim najczęściej pojawia się „a” – z częstotliwością w przybliżeniu \(9\%.\) Bez litery „e” w języku francuskim nie da się powiedzieć podstawowych słów, jak „matka”, „ojciec”, „rodzina” (nie da się też rzucić merde!). Nie można też wypowiedzieć się bezpośrednio o sobie.

Są różne interpretacje owego „skazania” litery „e” na zagładę. Odniesienie się do nich znacznie przerastałoby rozmiary tego artykułu, jak i kompetencje autora. Warto, po przeczytaniu książki, zwrócić uwagę na posłowie, w którym tłumacze Renè Koelblen i Stanisław Waszak (matematyk i filolog, tłumacze piosenek) wyjaśniają różne aspekty książki i jej tłumaczenia. Tłumacze zrobili to, czego nie mógł zrobić Perec – korzystali z programu komputerowego. Podobnie jak Perec, skazali na zagładę literę „e”. Stosowali na przykład zasadę, że zamiast „zrobiłem” występuje „zdarzyło mi się zrobić”. W hiszpańskim tłumaczeniu unicestwieniu uległa litera „a”.

Plac Pereca w Paryżu

G. Perec, Życie instrukcja obsługi, Lokator, 2021.

Michał Paweł Markowski, Georges Perec: zapisywanie pustki, Tygodnik Powszechny, nr 28, 2766, 14 lipca 2002.

Omówienie skomplikowanej struktury matematycznej w książce Pereca Życie instrukcja obsługi zdecydowanie wykracza poza ramy tego artykułu. Perec opisuje w niej historię mieszkańców \(10\)–piętrowej kamienicy, gdzie na każdym piętrze jest \(10\) mieszkań. Perec narzucił sobie pewne ścisłe reguły, których w większości Czytelnik zapewne nie zauważy. Niemniej reguły te są skrupulatnie przestrzegane. Na przykład sposób poruszania się po mieszkaniach kamienicy oparty jest na ruchu konika szachowego, każde pole (mieszkanie) przechodzimy tylko raz.

R. C. Bose, E.T. Parker, S.S. Shrikhande, Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler’s conjecture, Canadian Journal of Mathematics 12, 1960.

H.H. Frisinger, The solution of a famous two–centuries–old problem: The Leonhard Euler–Latin Square Conjecture, Historia Mathematica 8, 1981.

Aspektem kombinatorycznym struktury książki jest rozmieszczenie w mieszkaniach elementów różnych rodzajów: kolorów, biżuterii, tkanin… Perec stworzył listy 10 elementów wybranych rodzajów i połączył te listy w pary. W ramach każdej takiej pary starał się tak rozmieścić wszystkie możliwe dwójki elementów (po jednym z obu rodzajów) w mieszkaniach, by „możliwości nie powtarzały się w wierszach i kolumnach”. Zagadnienie nawiązuje do hipotezy Eulera, który przypuszczał, że taki sposób rozmieszczania jest niemożliwy (dla układu \(10\times 10\) czy ogólniej \((4k+2)\times(4k+2)\)). W roku 1959 Bose, Parker, Shrikhande udowodnili, że Euler nie miał racji: jest to możliwe! Więcej informacji o tej ciekawej historii można znaleźć w artykule Karola Gryszki z \(\Delta^{7}_{24}\), a także w tekstach przytoczonych na marginesie.

Książka Życie instrukcja obsługi została uznana przez opiniotwórcze czasopismo francuskie Le Monde za jedną ze 100 najważniejszych powieści XX wieku.

I. Calvino, Jeżeli \(t=0\), PIW, Warszawa 2021.

Jednym z najwybitniejszych pisarzy włoskich był Italo Calvino. W Opowieściach kosmikomicznych są wprost fajerwerki fantazji i humoru. Bohaterem i narratorem jest mający wiek Wszechświata Qfwfq, przeżywający niesamowite przygody. Bazą są naukowe, lub paranaukowe, teorie. Na przykład historia „Wszystko w jednym punkcie” odnosi się do Wielkiego Wybuchu. Książka pokazuje, że ścisłość i abstrakcję naukową można połączyć z finezją i dowcipem. Opowiadanie „Hrabia Monte Christo” w zbiorku Jeżeli \(t=0\) nawiązuje do książki Alexandra Dumasa z 1844 roku. Jest to historia więźnia osadzonego w hipersferycznym więzieniu, z którego nie może się wydostać. Jeżeli zdołam zbudować w myśli twierdzę, z której nie sposób uciec, ta wymyślona twierdza albo będzie tożsama z prawdziwą – w takim przypadku jest pewne, że nigdy się stąd nie wydostaniemy; ale przynajmniej zyskamy spokój kogoś, kto wie, że tkwi tutaj, ponieważ nie mógłby znajdować się gdzie indziej…

I. Calvino, Opowieści kosmikomiczne, Muza, 1996.

I. Calvino, Niewidzialne miasta, WAB, Warszawa 2013.
Polski tytuł zbiorku odbiega od włoskiego – Ti con zero, czyli \(T_0.\)

Niewidzialne miasta, to książka opowiadająca o spotkaniu Marca Polo z Kubilaj-Chanem (Kubłaj-Chanem). Obie postacie są historyczne i rzeczywiście mogło dojść do ich spotkania. Marco Polo był podróżnikiem z Wenecji opisującym (i, jak się uważa, „kolorującym”) swoje podróże, a Kubilaj-Chan – wnukiem Czyngis-Chana i władcą jednego z największych imperiów w historii świata. Marco Polo opowiada władcy o miastach jego imperium, których on, władca, nigdy nie widział. Każdy rozdział zawiera pięć opisów miast, z których każde ma nazwę będącą żeńskim imieniem i każde jest z odniesieniem do kultury, języka, czasu, pamięci, śmierci i doświadczenia ludzkiego. Struktura książki jest wyraźnie oparta na wzorcach matematycznych. Oto kończący fragment z książki Niewidzialne miasta, odpowiedni na ponure czasy: Piekło żyjących nie jest czymś, co nastanie; jeśli istnieje, jest już tutaj, jest piekłem, w którym żyjemy na co dzień, które tworzymy, przebywając razem. Są dwa sposoby, aby nie sprawiało ono cierpień. Pierwszy jest nietrudny dla wielu ludzi: zaakceptować piekło i stać się jego częścią, aż przestanie się je dostrzegać. Drugi jest ryzykowny i wymaga ciągłej uwagi i ćwiczenia: odszukać i umieć rozpoznać, kto i co pośród piekła piekłem nie jest, i utrwalić to, i rozprzestrzenić.