Afiliacja: Politechnika Śląska
Jedną z najbardziej ludzkich cech jest kolekcjonerstwo. Gromadzenie
i porządkowanie przedmiotów może dawać poczucie ładu w – bywa, że dość
chaotycznej – codzienności. Ludzie od niepamiętnych czasów kolekcjonują najrozmaitsze rzeczy: od znaczków pocztowych po tosty z wizerunkami
świętych.
Skoro o znaczkach mowa, nie sposób przy tej okazji nie wspomnieć, że pewne małżeństwo matematyków z Krakowa słynie m.in. z bardzo pokaźnej kolekcji znaczków pocztowych o tematyce matematycznej.
Amerykański podróżnik i dziennikarz Marcus Baker, jeden z założycieli National Geographic, w 1885 roku – kilka lat przed powstaniem tego popularnego czasopisma – zasłynął jako osobliwy kolekcjoner. W prestiżowym Annals of Mathematics opublikował dwuczęściowy artykuł pod tytułem A collection of formulæ for the area of a plane triangle, zawierający \(110\) różnych wzorów na pole trójkąta (zliczając je zgodnie z zasadą mówiącą, że pole trójkąta wyrażone przez połowę iloczynu długości boku i opadającej na niego wysokości to jeden wzór, a nie trzy!).
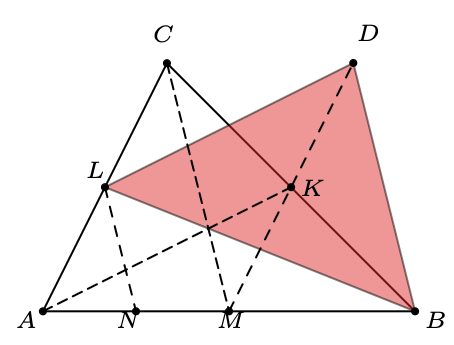
Mimo kilku błędów kolekcja jest bardzo urokliwa. Zaczyna się od trzech wariantów wzoru Herona – wersji z bokami (czyli tej najbardziej znanej), po której zaprezentowano warianty ze środkowymi i z wysokościami. Mamy zatem \[\mathtt{{\bf 1.}}\ \Delta=\sqrt{s(s-a)(s-b)(s-c)},\] gdzie \(a,b,c\) są długościami boków, a \(s\) oznacza połowę obwodu. Następnie, jeżeli \(m_a,\) \(m_b\) i \(m_c\) to środkowe odpowiednich boków, a \(\sigma\) to połowa ich sumy, to \[\mathtt{{\bf 2.}}\ \Delta=\frac43\sqrt{\sigma(\sigma-m_a)(\sigma-m_b)(\sigma-m_c)}.\] Poprawność tego wzoru można sprawdzić na przykład poprzez porównanie z polem trójkąta o bokach \(m_a,\) \(m_b\) i \(m_c.\) Istotnie, na rysunku na marginesie punkty \(K,\) \(L\) i \(M\) są środkami odpowiednich boków trójkąta \(ABC,\) punkt \(N\) to środek odcinka \(AM,\) zaś punkt \(D\) to odbicie symetryczne punktu \(M\) względem \(K.\) Boki trójkąta \(LBD\) przystają do odpowiednich środkowych trójkąta \(ABC.\) Jednocześnie pole \(LBD\) jest równe polu \(NBD,\) a ono z kolei jest równe 3/4 pola trójkąta \(ABC.\) Uzupełnienie szczegółów tego rozumowania pozostawiam Czytelnikowi.
Artykuł został napisany dość nonszalancko – Baker podał listę wzorów, nie dowodząc ani jednego z nich. W kolekcji znajduje się około trzydziestu wzorów z błędami.
Trzeci wzór Herona został przez Bakera zapisany w trochę innym stylu: \[\mathtt{{\bf 3.}}\ \Delta=\frac1{\sqrt{\left({\frac1{h_a}+\frac1{h_b}+\frac1{h_c}}\right)\left({-\frac1{h_a}+\frac1{h_b}+\frac1{h_c}}\right)\left({\frac1{h_a}-\frac1{h_b}+\frac1{h_c}}\right)\left({\frac1{h_a}+\frac1{h_b}-\frac1{h_c}}\right)}}.\] Można go uzasadnić poprzez zastosowanie we wzorze Herona podstawień typu \(h_a=\frac{2\Delta}a.\)
Trzeci wzór w duchu dwóch poprzednich można wyrazić następująco: Jeżeli \(\frac1{h_a},\ \frac1{h_b}\) i \(\frac1{h_c}\) to odwrotności wysokości trójkąta, a \(\frac1h\) to połowa ich sumy, to pole trójkąta wynosi: \[\Delta=\frac1{4\sqrt{\frac1h\left(\frac1h-\frac1{h_a}\right)\left(\frac1h-\frac1{h_b}\right)\left(\frac1h-\frac1{h_c}\right)}}.\] Ze względu na ograniczenia przestrzenne Kąta Otwartego pomińmy 106 formuł i przedstawmy ostatni okaz z listy Bakera: \[\mathtt{{\bf 110.}}\ \Delta=\frac{2R}r\cdot N,\] gdzie \(r\) i \(R\) to promienie okręgów, odpowiednio, wpisanego i opisanego, oraz \(N\) to pole trójkąta, którego wierzchołkami są punkty styczności okręgu wpisanego z bokami trójkąta.
Czytelnika Zaintrygowanego tą opowieścią zachęcam do odnalezienia artykułu Bakera i samodzielnego sprawdzenia, co się kryje między trzecim a sto dziesiątym wzorem w tej osobliwej kolekcji.