Zadania z matematyki nr 911, 912
Redaguje Marcin E. KUCZMA
911. Dane są liczby naturalne \(m\) (parzysta), \(n\) (nieparzysta); \(n\ge3.\) Prostokąt o bokach długości \(m,n,\) podzielony na \(mn\) pól (kwadratów jednostkowych) należy pokryć płytkami dwóch typów \(L\) i \(N,\) nakrywającymi (odpowiednio) trzy oraz cztery pola: płytka typu \(L\) to kwadrat \({2\times2}\) z usuniętym jednym polem; płytka typu \(N\) to prostokąt \({3\times2}\) z usuniętymi dwoma przeciwległymi polami narożnymi (dotykającymi końców przekątnej prostokąta \({3\times2}\)). Płytki mogą być dowolnie obracane, ale nie mogą na siebie nachodzić ani wystawać poza obręb danego prostokąta \({m\times{n}}.\) Wyznaczyć minimalną liczbę płytek typu \(L,\) jaka może być użyta w takim parkietażu.
912. W czworościanie \(ABCD\) krawędzie \(AB\) i \(CD\) są równej długości, a prosta przechodząca przez środki tych krawędzi jest prostopadła do każdej z nich. Udowodnić, że dla każdej liczby \({r>0}\) istnieje taka sfera o promieniu \(r,\) że dla wszystkich punktów \(P,\) leżących na tej sferze, suma \({PA^2+PB^2+PC^2+PD^2}\) ma jednakową wartość.
Zadanie 912 jest nieznacznie rozszerzoną wersją propozycji, jaką przysłał pan Mirosław Matlęga ze Skoczowa.
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
901 (\(WT = 1{,}33\)) i 902 (\(WT = 1{,}90\))
z numeru 5/2025
Krzysztof Maziarz Londyn 44,20 Jerzy Cisło Wrocław 43,28 Szymon Kitowski 41,11 Andrzej Daniluk Warszawa 40,76 Barbara Mroczek 40,24 Krzysztof Kamiński Pabianice 38,09 Mikołaj Znamierowski 37,87 Marian Łupieżowiec Gliwice 37,09 Roksana Słowik 35,92 Michał Adamaszek Kopenhaga 34,49 Stanisław Bednarek Łódź 34,43 Pan Krzysztof Maziarz: drugie okrążenie, czekamy na dalsze!
Zadania z fizyki nr 808, 809 Termin nadsyłania rozwiązań: 28 II 2026
Redaguje Elżbieta ZAWISTOWSKA
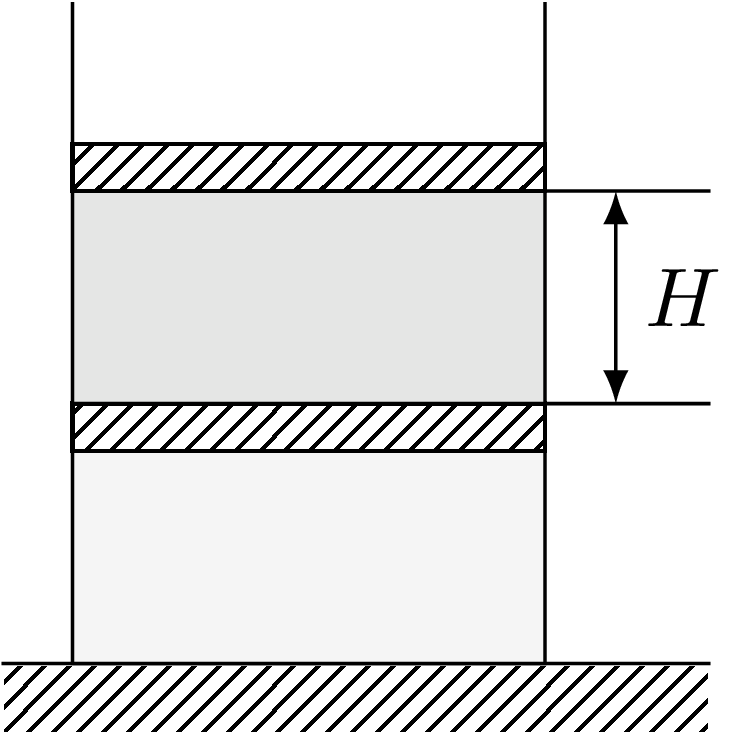
808. Pionowe naczynie zawiera dwie porcje gazu w stanie równowagi oddzielone od siebie i otaczającej przestrzeni dwoma jednakowymi ciężkimi tłokami. W górnej części naczynia znajduje się tlen, w dolnej hel. Na zewnątrz naczynia jest próżnia, gaz nie oddaje ciepła do otoczenia. Przewodnictwo cieplne tłoka rozdzielającego naczynia jest bardzo małe. Na początku objętości gazów są jednakowe, a odległość między tłokami wynosi \(H.\) Hel jest wolno ogrzewany i jego objętość rośnie dwukrotnie. Jaka będzie odległość między tłokami po długim czasie, gdy osiągnięty zostanie ponownie stan równowagi? Ciepło przekazywane do górnej części naczynia w czasie ogrzewania możemy zaniedbać.
809. W ustalonym położeniu obiektywu w aparacie fotograficznym głębia ostrości obejmuje zakres odległości przedmiotów od \(d_{1}=15\) m do \(d_{2}=30\) m. Po zmniejszeniu otworu przesłony dolna granica głębi ostrości osiągnęła wartość \(d'_{1}=10\) m. Znaleźć jej górną granicę.
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
798 (\(WT=2{,}97\)), 799 (\(WT=3{,}01\))
z numeru 5/2025
Jacek Konieczny Poznań 41,41 Jan Zambrzycki Białystok 4 – 37,68 Ryszard Woźniak Kraków 34,00 Andrzej Nowogrodzki Chocianów 3 – 32,28 Paweł Perkowski Ożarów Maz. 6 – 25,64 Krzysztof Zygan Lubin 22,09 Tomasz Wietecha Tarnów 18 – 20,06 Paweł Kubit Kraków 19,62