Afiliacja: V Liceum Ogólnokształcące im. Augusta Witkowskiego w Krakowie
Czy wiedzieliście, że pole trójkąta prostokątnego można obliczyć ze wzoru \(P=ab\)? Nie, nie zapomnieliśmy tutaj o dzieleniu przez 2. I nie, ani \(a,\) ani \(b\) nie są tu sztucznymi wielkościami w stylu „długość boku podzielona przez \(\sqrt{2}\)”. Nie są to również żadne magiczne długości, lecz po prostu odległości końców przeciwprostokątnej od punktu jej styczności z okręgiem wpisanym. Na pierwszy rzut oka wzór może wydawać się podejrzanie prosty, jak się jednak za chwilę okaże, kryje się za nim elegancka, elementarna geometria.
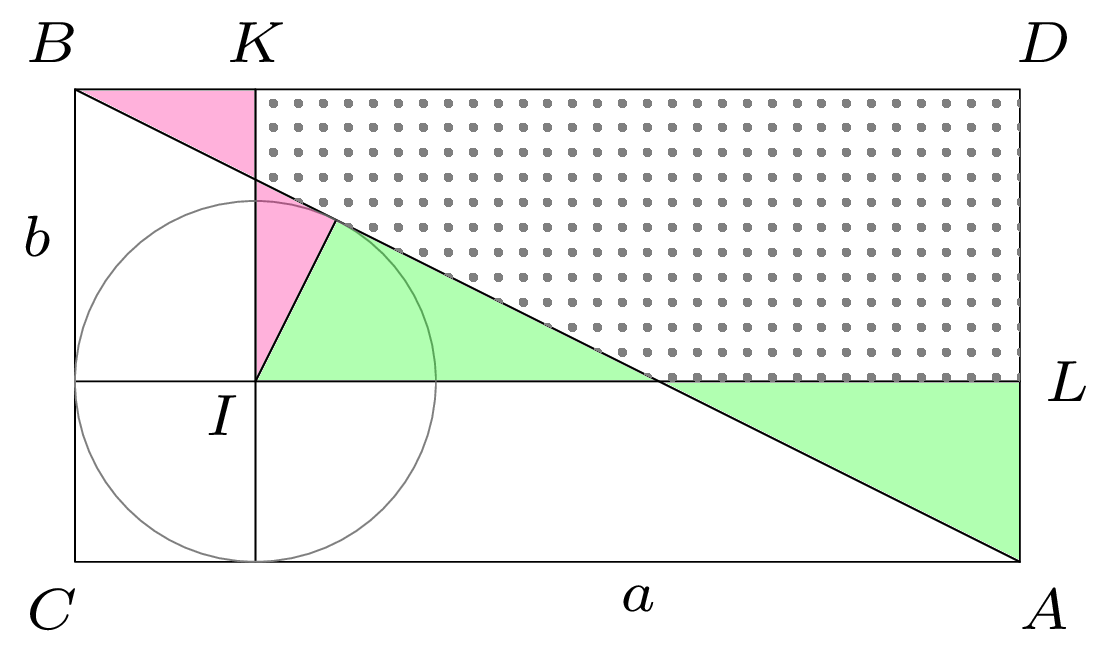
Rozważmy trójkąt prostokątny \(ABC\) o kącie prostym w wierzchołku \(C\) i niech \(a\) i \(b\) będą odległościami punktów, odpowiednio, \(A\) i \(B\) od punktów styczności okręgu wpisanego w trójkąt. Wybierzmy punkt \(D\) tak, by \(ACBD\) był prostokątem, ponadto przez środek \(I\) okręgu wpisanego poprowadźmy proste równoległe do przyprostokątnych trójkąta. Zaznaczone na rysunku pary trójkątów różowych i zielonych są przystające (cecha kąt-bok-kąt). Z jednego trójkąta różowego, jednego zielonego i zakropkowanego pięciokąta można złożyć zarówno prostokąt \(KILD\) o polu \(ab,\) jak i trójkąt \(BAD,\) przystający do trójkąta \(ABC.\) Prawda, że ładne?