Zadania

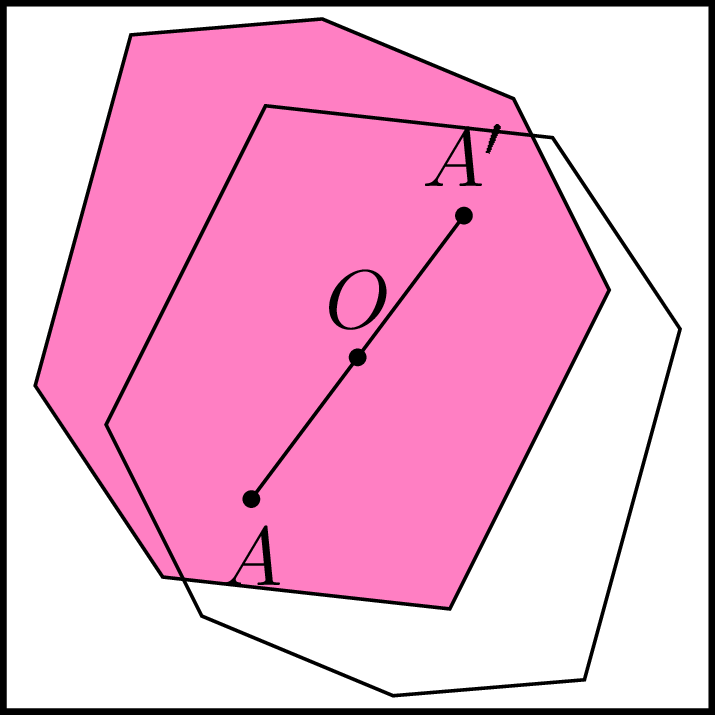
Niech \(\mathcal{R}\) będzie dowolną kopią \(\mathcal{P}\) umieszczoną w kwadracie \(\mathcal{K}.\) Rozważmy figurę \(\mathcal{R}'\) będącą obrazem figury wypukłej \(\mathcal{R}\) przy symetrii względem środka \(O\) kwadratu. Wówczas \(\mathcal{R}'\) znajduje się wewnątrz \(\mathcal{K}\) oraz zgodnie z założeniem \(\mathcal{R}\) i \(\mathcal{R}'\) mają punkt wspólny \(A.\) Obraz \(A'\) punktu \(A\) przy symetrii względem \(O\) również znajduje się w przecięciu wielokątów \(\mathcal{R}\) i \(\mathcal{R}'.\) Ponieważ punkt \(O\) leży na odcinku łączącym dwa punkty należące do wielokąta wypukłego \(\mathcal{R},\) sam też do niego należy. Pokazaliśmy, że dowolna kopia wielokąta \(\mathcal{P}\) umieszczona w kwadracie \(\mathcal{K}\) zawiera punkt \(O,\) skąd w prosty sposób wynika teza.

Niech dla \(m=1,2,\ldots,n-1\)\[S_{m}:=\sum\limits_{i=1}^m a_i-\sum\limits_{i=m+1}^n a_i\] i przyjmijmy \(S_{n}=-S_0=\sum\limits_{i=1}^n a_i.\) Wtedy \[S_{m}-2a_{m}=S_{m-1}.\] Rozpatrzmy ciąg \[S_{n},\;S_{n-1}, \;\ldots,\;S_{1},\;S_{0}.\] Bez straty ogólności możemy założyć, że \(S_{n}>0.\) Wówczas \(S_0<0,\) możemy zatem znaleźć takie \(i\geq 1,\) że \(S_{i}\geq 0\geq S_{i-1}.\)

Przypuśćmy, że \(S_{i}=|S_{i}|> | a_{i}|\) i \(-S_{i-1}=| S_{i-1} |> | a_{i} |.\) Ponieważ \(S_{i}-2a_{i}=S_{i-1}\), to \(-S_{i}+2a_{i}> | a_{i} |,\) więc \(2a_{i}>S_{i}+ | a_{i} |>2 | a_{i} |,\) co jest niemożliwe.

Załóżmy przeciwnie, czyli \[\omega(an + c) < \omega(bn + c).\] dla dowolnej liczby całkowitej \(n>0.\) Dla ustalonej liczby całkowitej \(k>0,\) w powyższej nierówności, podstawiając za \(n\) liczby \[a^{k-1},\; a^{k-2}b,\; a^{k-3}b^2,\; \ldots,\; ab^{k-2},\; b^{k-1},\] dostajemy ciąg nierówności \[\omega(a^k + c)<\omega(a^{k-1}b + c)<\ldots <\omega(b^k + c).\] Wynika stąd, że \(\omega(b^k + c)\geq k+1.\) Ponieważ iloczyn \(k+1\) liczb pierwszych jest większy niż \(k!,\) więc \[k!<b^k+c <b^k + c^k <(b+c)^k.\] Jednakże \[\lim_{n\to +\infty}\sqrt[k]{k!}=+\infty \;\;\; \textup{(sprawdź to!),}\] więc \(\sqrt[k]{k!}\) dla dużych \(k\) przekracza \(b+c\) – sprzeczność.

W komorze silnika rakietowego następuje bardzo gwałtowne spalanie paliwa. Gazowe produkty tego spalania wypływają z dużą prędkością przez dyszę silnika. Prędkość \(u,\) z jaką wylatują z dyszy, odpowiada w przybliżeniu średniej prędkości cząsteczek gazu – produktu spalania – o temperaturze \(T\) panującej w komorze silnika. Na podstawie twierdzenia o ekwipartycji energii znamy średnią energię kinetyczną cząsteczek gazu: \[\frac{1}{2}mu^2 = \frac{3}{2}kT.\] W powyższym wzorze \(m\) oznacza masę cząsteczki, a \(k\) stałą Boltzmanna. Otrzymujemy oszacowanie: \[u = \sqrt{\frac{3kT}{m}} = \sqrt{\frac{3RT}{\mu}}.\] W ostatniej równości \(R\) oznacza uniwersalną stałą gazową, \(R = 8{,}3145\) J/(mol\(\cdot\)K), a \(\mu\) molową masę produktów spalania. Wynika stąd, że produkty spalania powinny być jak ,,najlżejsze” (o małej warotści \(\mu\)), a temperatura \(T\) w komorze spalania powinna być jak najwyższa. Maksymalna wartość temperatury ograniczana jest przez wytrzymałość scianek silnika – zwykle niewielkie kilka tysięcy kelwinów. W silniku RS-25 napędzającym promy kosmiczne (Space-Shuttle) paliwem jest mieszanina ciekłego tlenu (O\(_2\)) i wodoru (H\(_2\)). Produktem spalania jest woda (H\(_2\)O) o molowej masie \(\mu = 18\) g. W komorze silnika (poza atmosferą) osiągana jest temperatura około 3250 K. Według naszego oszacowania \({u \approx 2{,}1}\) km/s. W rzeczywistości osiągana prędkość gazów to około 4,4 km/s. Różnica wynika głównie z przemian stanu gazu zachodzących w odpowiednio ukształtowanej dyszy silnika (tzw. dyszy Lavala) podczas wypływu gazu zwiększających uzyskiwaną prędkość.

Zgodnie z tzw. wzorem Ciołkowskiego prędkość rakiety o masie początkowej \(m_0\) wzrasta o \(\Delta v,\) zgodnie ze wzorem: \[\Delta v = u\ln\biggl(\frac{m_0}{m_f}\biggr),\] w którym \(u\) oznacza prędkość gazów wyrzucanych przez silnik, a \(m_f\) masę końcową rakiety. Oznacza to, że po osiągnięciu I prędkości kosmicznej, \(\Delta v = v_1,\) masa rakiety \(m_f\) będzie wynosiła: \[m_f = m_0\exp\biggl(-\frac{v_1}{u}\biggr).\] Stosunek masy zużytego paliwa \(m_0 - m_f\) do masy początkowej \(m_0\) wyniesie więc: \[\frac{m_0 - m_f}{m_0} = 1 - \exp\biggl(-\frac{v_1}{u}\biggr).\] Liczbowo, dla danych z treści zadania, stosunek masy paliwa do początkowej masy rakiety \({(m_0 - m_f)/m_0 \approx 0{,}865}.\) Podczas startu z powierzchni Ziemi, ze względu na konieczność pokonania przyciągania ziemskiego i oporu powietrza, stosunek ten byłby jeszcze bliższy jedności.