* Instytut Matematyki, Uniwersytet Jagielloński
W latach 1991–1997 redaktor naczelny samodzielnej kolumny Epsilon w Delcie.
Od 1996 roku członek Komitetu Redakcyjnego Delty, w latach 2004–2019 jego wiceprzewodniczący, od roku 2019 przewodniczący.
Jednym z moich ulubionych numerów Delty jest ten z czerwca 1986 roku (\(\Delta^{6}_{86}\)). Z okazji jubileuszu (był to numer 150) został praktycznie w całości wypełniony krótkimi ciekawostkami matematycznymi, fizycznymi i astronomicznymi, których, jak nietrudno zgadnąć, Redakcja umieściła 150.
Czy coś opisanego w opublikowanych wówczas matematycznych ciekawostkach mogło po 37 latach ulec zmianie? Jedną z największych zalet matematyki jest dla mnie to, że twierdzenie raz udowodnione (poprawnie) pozostaje prawdziwym do końca świata. Na przykład w ciekawostce nr 122 podano, że jeśli obrócimy sześcian wokół jego przekątnej, to otrzymamy bryłę złożoną z dwóch stożków i hiperboloidy obrotowej. Tak było wówczas, gdy terminu ,,hiperboloida obrotowa” jeszcze nie wprowadzono, tak było w 1986 roku, tak jest teraz i tak będzie zawsze. Jednak w ciągu tych 37 lat w matematyce także co nieco (a nawet wiele) się zmieniło. Wtedy nie wiedzieliśmy jeszcze, że Wielkie Twierdzenie Fermata jest prawdziwe (o nim w numerze 6/1986 mowy nie było), a największą znaną liczbą pierwszą (tego tematu też nie poruszono) była wówczas \(2^{216091}-1\); we wrześniu 2023 tę rolę pełni \(2^{82589933}-1\). Postęp w tym zakresie zobrazowany jest na przykład przez to, że gdybyśmy największą znaną w 1986 roku liczbę pierwszą zapisali na pasku papieru taką czcionką, jaką wydrukowany jest ten tekst w Delcie, zajęłoby to około 114 metrów. W przypadku obecnej rekordzistki – ponad 43 kilometry. A liczby to wielkie nad wyraz – napisana na takim pasku szacunkowa liczba atomów we Wszechświecie nie wypełniłaby nawet jednej linijki kartki A4.
O związku między sześcianem a hiperboloidą obrotową pisze również Marek Kordos na stronie 3 – przyp. red.
Także w przypadku kilku ,,deltowych ciekawostek” sprzed 37 lat można dziś powiedzieć coś więcej… O tym będzie mowa.
Oczywiste jest, że w kwadracie o wymiarach \(n \times n\) możemy tak ułożyć \(n^2\) kwadratów o boku 1, by ich wnętrza były parami rozłączne – nazwijmy takie umieszczenie małych kwadratów ,,dobrym”. Czy w sytuacji, gdy nieznacznie (o mniej niż 1) zwiększymy bok dużego kwadratu, można weń w dobry sposób włożyć więcej kwadratów jednostkowych? Nie da się tego zrobić, gdy będziemy je układać ,,standardowo”, czyli tak, by ich boki były równoległe do boków dużego kwadratu. Można je jednak umieścić inaczej… Na rysunkach poniżej pokazane są schematy takiego ułożenia. W kwadracie o boku \(3 + \frac{\sqrt{2}}{2}\) (w przybliżeniu \(3{,}71\)) zmieścimy \(3^2 + 1\) kwadratów jednostkowych (rys. 1). W kwadrat o boku \(5 + \frac{5\sqrt{2}}{2}\) (w przybliżeniu \(8{,}54\)) można włożyć \(8^2 + 1\) kwadratów jednostkowych (rys. 2). W tej sytuacji niepokryte pole w kwadracie wynosi \(\frac{50\sqrt{2}-55}{2}\), czyli w przybliżeniu \(7{,}86\).
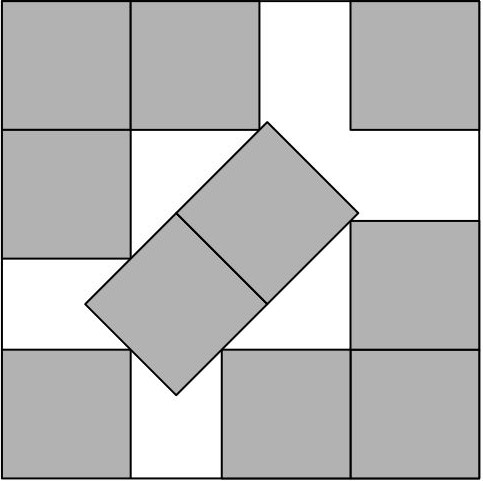
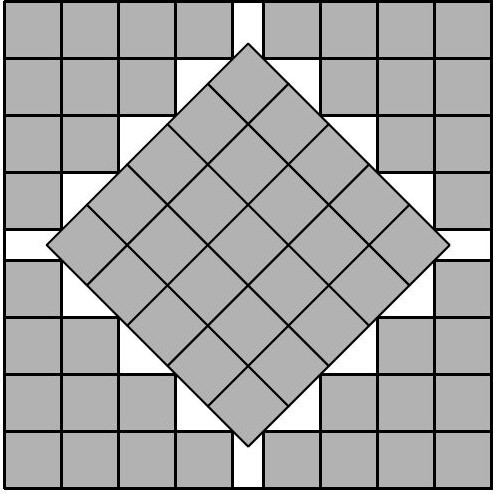
Gdy \(n\) jest odpowiednio duże, można wkładać małe kwadraty jeszcze bardziej oryginalnymi metodami, a w konstrukcji odpowiednio wykorzystywać równoległoboki, trapezy… Powstaje naturalne pytanie: jak małe może być pole (oznaczmy je przez \(W(x)\)), które musi pozostać niepokryte przy umiejętnym ułożeniu kwadratów jednostkowych w kwadracie o boku \(x\), przy czym \(x\) nie musi być liczbą naturalną. Formalnie:
\(W(x) = x^2 - \sup\{ P \colon P\) jest liczbą kwadratów jednostkowych, które możemy umieścić w ,,dobry” sposób w kwadracie o boku \(x\}\).
Wymienieni w tekście matematycy mają w swym dorobku liczne znaczące osiągnięcia. Na marginesie podam jedynie ich daty życia.
Paul Erdős (1913–1996)
Ronald Lewis Graham (1935–2020)
Hugh Lowell Montgomery (ur. 1944)
Tę liczbę zaczęli badać Paul Erdős i Ronald Graham. W 1974 roku wykazali oni istnienie takiej stałej \(C\), że dla odpowiednio dużych \(x\) zachodzi oszacowanie \(W(x) \le C\cdot x^{7/11}\) (jeśli użyjemy ciut bardziej zaawansowanej terminologii, zapisujemy to jako \(W(x) = O(x^{7/11})\)). W 1986 roku znano oszacowanie nieznacznie wzmocnione (o tym była mowa w ciekawostce nr 4). Liczba \(x^{7/11}\) została zastąpiona przez \(x^{(3-\sqrt{3})/2}\); dokonał tego Hugh Montgomery, który jednak swojego rezultatu nie opublikował.
Można rozważać oszacowanie niepokrytego pola od dołu. Klaus Roth (medalista Fieldsa z 1958 roku) i Robert Vaughan podali w 1978 roku odpowiednie ograniczenia, rozwiązując problem postawiony przez Erdősa i Grahama. Z ich rezultatu wynikało, że \(W(n+\frac{1}{2})\) zawsze jest większe od \(\sqrt{n}\).
Klaus Friedrich Roth (1925–2015)
Robert Vaughan (ur. 1945)
Fan Chung (ur. 1949)
Oszacowanie Montgomery’ego w kolejnych latach wzmacniano. Ronald Graham i jego żona Fan Chung udowodnili, że \(W(x) = O(x^{(3+\sqrt{2})/7}\cdot \log x)\). A ,,jeszcze ciepły” wynik Chung i Grahama, opublikowany w 2020 roku, mówi, że \(W(x) = O(x^{3/5})\).
Liczba \(\frac{7}{11}\) to w przybliżeniu \(0{,}6364\), w oszacowaniu Montgomery’ego mamy w wykładniku \(0{,}6334\). Chung i Graham doszli do liczby \(0{,}6\). W swojej pracy stawiają kolejne problemy. W szczególności stwierdzili, że rezultat Rotha i Vaughana pozwala zapytać, czy przypadkiem nie zachodzi związek \(W(x) = O(x^{\frac{1}{2}})\), niemniej oni w to nie wierzą… Za wykazanie (lub obalenie) tego, że \(W(x) = O(x^{\frac{3}{5}-c})\) dla pewnej stałej \(c,\) zaoferowali 250 dolarów.
Przejdźmy teraz do ciekawostki nr 86. Zacytujmy: Spróbujmy ustawić 36 wojskowych (po 6 z sześciu jednostek i po sześciu w tym samym stopniu, przy czym reprezentację jednostki stanowią wojskowi różnych stopni) na polach szachownicy \(6 \times 6\) tak, by wszyscy stojący w szeregu czy w kolumnie byli różnych stopni i z różnych jednostek. Albo lepiej nie próbujmy – to na pewno się nie uda. Podana została też informacja, że w przypadku pewnych kwadratów \(n \times n\) da się to zrobić, ale w przypadku np. 10-osobowych reprezentacji dziesięciu jednostek problem jest wciąż otwarty.
A \(\alpha\) B \(\gamma\) C \(\beta\) C \(\gamma\) A \(\beta\) B \(\alpha\) B \(\beta\) C \(\alpha\) A \(\gamma\) Rys. 3
Nie zostało wtedy w Delcie wspomniane, że autorem zadania o 36 wojskowych jest nie kto inny, jak Leonhard Euler. Pytanie to postawił w 1779 roku. W przypadku dwóch jednostek łatwo zauważyć, że odpowiednie ustawienie nie jest możliwe, w przypadku trzech zadanie jest bardzo proste (rys. 3). Euler potrafił stosownie rozmieścić żołnierzy dla \(n=4\) i \(n=5\), jednak po bezskutecznych próbach konstrukcji dla \(n=6\) wyraził w 1782 roku przypuszczenie, że w tym przypadku jest to niewykonalne. Na dowód trzeba było czekać ponad 100 lat… Opublikował go w 1901 roku Gaston Tarry. Obecnie za pomocą komputerów poradzilibyśmy sobie z problemem bez większych kłopotów.
Leonhard Euler (1707–1783)
Gaston Tarry (1843–1913)
Raj Chandra Bose (1901–987)
Sharadchandra Shankar Shrikhande (1917–2020)
Ernest Tilden Parker (1926–1991)
Już Euler wiedział, że można odpowiednio rozlokować żołnierzy w przypadkach \(n\) nieparzystych oraz podzielnych przez 4. Sądził, że jest to niemożliwe dla liczb postaci \(4k+2\). Okazało się jednak, że jest inaczej.
W 1986 roku w Polsce dostęp do rozmaitych czasopism matematycznych był nad wyraz ograniczony – okazuje się, że Redakcja Delty nie dysponowała pełną informacją, gdyż problem w przypadku \({n=10}\) był już wtedy (jak zresztą we wszystkich innych przypadkach) rozstrzygnięty. W 1959 roku Raj Bose, Sharadchandra Shrikhande i Ernest Parker udowodnili, że można odpowiedniego ustawienia dokonać dla wszystkich parzystych \(n\) niepodzielnych przez 4 i większych od 6. Warto wspomnieć, że artykuł (artykuł, nie krótka wzmianka) opowiadający o ich wyniku został opublikowany 26 kwietnia 1959 roku na łamach dziennika New York Times.
Odpowiednie ustawienie dla \(n=10\) pokazane jest na marginesie.
B C J D F E A I H G \(\beta\) \(\delta\) \(\alpha\) \(\vartheta\) \(\varepsilon\) \(\iota\) \(\eta\) \(\gamma\) \(\lambda\) \(\zeta\) A J G F D I E C B H \(\vartheta\) \(\lambda\) \(\delta\) \(\alpha\) \(\beta\) \(\varepsilon\) \(\gamma\) \(\eta\) \(\zeta\) \(\iota\) E A F H I D C G J B \(\eta\) \(\beta\) \(\zeta\) \(\delta\) \(\alpha\) \(\lambda\) \(\varepsilon\) \(\vartheta\) \(\iota\) \(\gamma\) G E G I B C D H F J \(\varepsilon\) \(\vartheta\) \(\lambda\) \(\iota\) \(\delta\) \(\alpha\) \(\zeta\) \(\beta\) \(\gamma\) \(\eta\) D H E A C J G B I F \(\iota\) \(\varepsilon\) \(\beta\) \(\zeta\) \(\gamma\) \(\delta\) \(\alpha\) \(\lambda\) \(\eta\) \(\vartheta\) H D B E A G F J C I \(\alpha\) \(\gamma\) \(\varepsilon\) \(\lambda\) \(\iota\) \(\eta\) \(\delta\) \(\zeta\) \(\vartheta\) \(\beta\) I B D J E A H F G C \(\delta\) \(\alpha\) \(\eta\) \(\varepsilon\) \(\zeta\) \(\gamma\) \(\vartheta\) \(\iota\) \(\beta\) \(\lambda\) J F I C G H B D A E \(\gamma\) \(\eta\) \(\vartheta\) \(\beta\) \(\lambda\) \(\zeta\) \(\iota\) \(\delta\) \(\alpha\) \(\varepsilon\) F I C G H B J A E D \(\lambda\) \(\zeta\) \(\iota\) \(\gamma\) \(\eta\) \(\vartheta\) \(\beta\) \(\varepsilon\) \(\delta\) \(\alpha\) C G H B J I F E D A \(\zeta\) \(\iota\) \(\gamma\) \(\eta\) \(\vartheta\) \(\beta\) \(\lambda\) \(\alpha\) \(\varepsilon\) \(\delta\) Rys. 4
O kwantowej wersji problemu ustawiania wojskowych można przeczytać w artykule 36 splątanych oficerów z Petersburga
w \(\Delta^3_{23}\).
Kolejną, której poświęcimy tu uwagę, jest ciekawostka nr 52. Rozważamy liczbę naturalną \(n\) i tworzymy rekurencyjnie ciąg: jeśli wyraz \(k\) jest liczbą parzystą, to następnym jest \(\frac{k}{2}\), jeśli nieparzystą – to \(3k+1\). W znanych przypadkach zawsze w pewnym momencie pojawia się jedynka (i potem konsekwentnie, okresowo, układ \(4, 2, 1\)). Czy tak jest zawsze? W 1986 roku wiadomo było, że tak się dzieje, jeśli pierwszy wyraz jest mniejszy od \(2^{40}\).
Hipotezę, że zawsze dojdziemy do jedynki, postawił w 1937 roku Lothar Collatz. Nazywana jest hipotezą Collatza, ale łączona jest też w nazwach z Ulamem, Kakutanim, Thwaitesem i Hassem… Żadne z tych nazwisk nie pojawiło się wtedy w Delcie, ale ciekawostki musiały być krótkie. Stanisław Ulam oraz Shizuo Kakutani zainteresowali się problemem i go rozpowszechniali, a Bryan Thwaites postawił go niezależnie od Collatza w 1952 roku. Można też w języku angielskim spotkać nazwę Syracuse Problem (tę nazwę zaproponował Helmut Hasse, gdy przedstawił go w latach pięćdziesiątych podczas wizyty na uniwersytecie w Syracuse; według innej wersji, problem przyciągnął uwagę matematyków z Syracuse na Międzynarodowym Kongresie Matematyków w Cambridge w 1950 roku – wtedy Collatz mówił o nim różnym uczestnikom Kongresu). Inna angielska nazwa to Hailstone Problem (hailstone to ziarenko gradu, a wyrazy ciągu się zwiększają i zmniejszają, jak ziarenka gradu w chmurze). Pojawiają się również terminy hailstone numbers oraz wondrous numbers (wondrous to cudowny, niezwykły). Paul Erdős, który wielokrotnie fundował nagrody za rozwiązanie rozmaitych problemów, za rozstrzygnięcie hipotezy Collatza oferował 500 dolarów. Nie był jedyny; przed nim, w 1970 roku, H.S.M. Coxeter ogłosił nagrodę w wysokości 50 dolarów, a później, w 1982 roku, Thwaites – 1000 dolarów.
Lothar Collatz (1910–1990)
Stanisław (Stan) Ulam (1909–1984)
Shizuo Kakutani (1911–2004)
Bryan Thwaites (ur. 1923)
Helmut Hasse (1898–1979)
Harold Scott MacDonald Coxeter (1907–2003)
David Bařina (ur. 1984)
Jedyną rzeczą, która w tym przypadku się zmieniła, jest katalog pierwszych wyrazów ciągów, dla których hipoteza jest prawdziwa. We wrześniu 2023 wiadomo, że dojdziemy do jedynki, jeśli zaczniemy od jakiejkolwiek liczby mniejszej od \(2^{70}\) (w przybliżeniu \(1{,}18\cdot 10^{21}\)). Prace nad większymi liczbami trwają (oczywiście z wykorzystaniem komputerów); intensywnie prowadzi je David Bařina z Brna.
Ciąg badany w hipotezie Collatza związany jest z wieloma pasjonującymi problemami i wynikami, ale to oddzielna sprawa.
Ostatnią ciekawostką, do której nawiążę, jest ta o numerze 115. Zacytuję w dokładnym brzmieniu: Niektórzy nazywają twierdzenie o trzech ciągach (jeśli \(a_n \le b_n \le c_n\) oraz \(\lim\limits_{n \to \infty} a_n = \lim\limits_{n \to \infty} c_n =g\), to ciąg \((b_n)\) jest zbieżny i \(\lim\limits_{n \to \infty} b_n =g\)) twierdzeniem o milicjantach i formułują je tak: Jeśli znajdziesz się między dwoma milicjantami idącymi do tego samego komisariatu, to też tam trafisz.
Tu też mamy istotną zmianę, bo milicji od dawna w Polsce nie ma…
Lat temu 37 – oprócz tego, że mi się to bardzo spodobało – zastanawiałem się, jak cenzura dopuściła do opublikowania tych słów. Wskazane jest wyjaśnienie dla młodszych Czytelników: przed 1989 rokiem wszystko, co miało zostać wydane drukiem, musiało być zatwierdzone przez Główny Urząd Kontroli Prasy, Publikacji i Widowisk, popularnie nazywany cenzurą. A kontrole przeprowadzano skrupulatnie i dotyczyły one także czasopism popularnonaukowych. Marek Kordos w wywiadzie udzielonym Epsilonowi opowiadał, że ingerencja cenzury pojawiła się już przy okazji tworzenia pierwszego numeru Delty. Umieszczono tam artykuł o Instytucie Badań Jądrowych w Krakowie i podano między innymi, ile Instytut zajmuje hektarów. Ta informacja okazała się wagi państwowej i należało ją skreślić. A na temat milicji – wracam do ciekawostki – można było wtedy pisać wyłącznie absolutnie pozytywnie, żarty nie wchodziły w grę…
Szczegóły: Z Markiem Kordosem o Delcie, Epsilon 11a, [w]: D.Ciesielska, K.Ciesielski, Z.Pogoda, Epsilon, Wydawnictwo Szkolne Omega, 2002. Angielska wersja wywiadu: European Mathematical Society Newsletter No. 41 (dostępne na stronie www European Mathematical Society).
Jak się później dowiedziałem, analogiczna nazwa istnieje (i nawet jest używana) w języku włoskim – teorema dei due carabinieri. Nie wiem, czy te nazwy powstały niezależnie od siebie i nie wiem, która jest wcześniejsza.
Może z okazji sześćdziesięciolecia Delty warto będzie sprawdzić, co się ewentualnie zmieniło w przypadku ciekawostek fizycznych i astronomicznych?