Klub 44

Oznaczmy $\measuredangle CAB=\alpha .$ Weźmy dowolną prostą $\ell$ i punkty $P,Q,X,$ jak w treści zadania. Rachunek kątów w trójkącie $ACP$ pokazuje, że $\measuredangle CPQ={90}^{\circ }-\alpha .$ Skoro $\measuredangle CPQ<{90}^{\circ },$ to punkt $X$ leży na półprostej $P{Q}^{\to }$ (na odcinku $PQ$ lub na jego przedłużeniu). Zatem także $\measuredangle CPX={90}^{\circ }-\alpha .$

Prowadzimy wysokość $CD.$ Usytuowanie punktów $A,D,P$ na prostej $AB$ może być różne (rysunki ilustrują dwie wybrane możliwości), ale dalsze rozumowanie nie zależy od konfiguracji. Okrąg o średnicy $CP$ przechodzi przez punkty $D$ oraz $X.$ Punkty $P$ i $D$ leżą po jednej stronie prostej $CX,$ skąd wynika, że $\measuredangle CDX=\measuredangle CPX={90}^{\circ }-\alpha .$

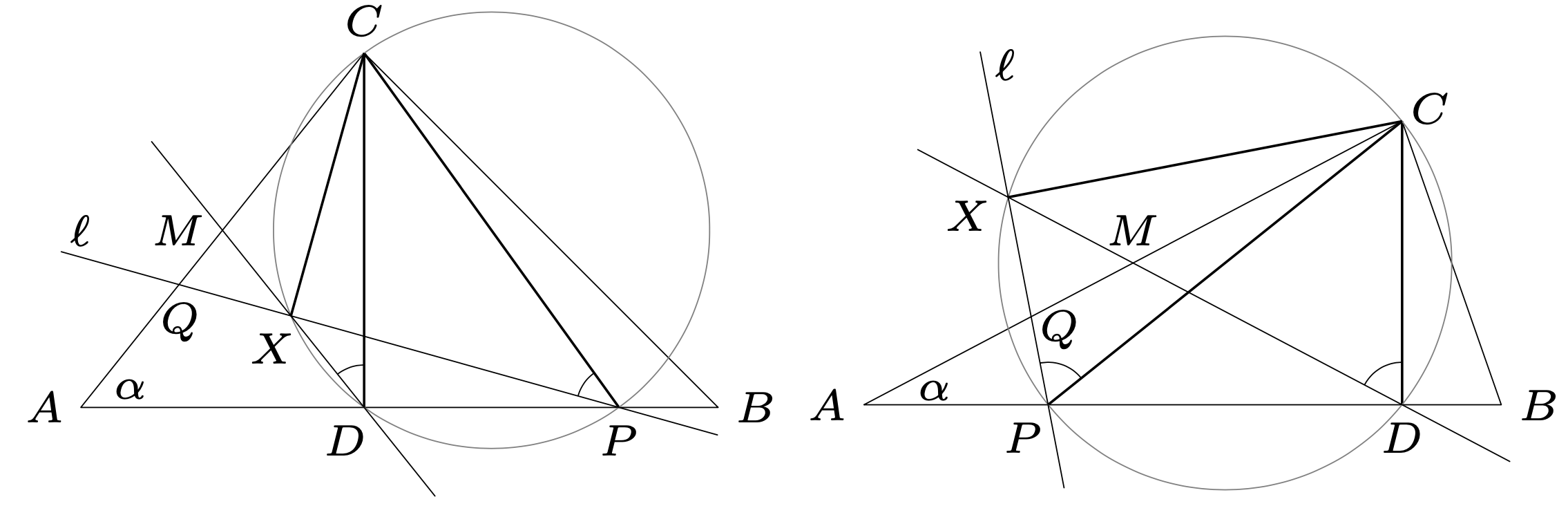
Prosta $DX$ przecina bok $AC$ w punkcie, który nazwiemy $M.$ Tak więc $\measuredangle ADM={90}^{\circ }-\measuredangle CDX=\alpha ,$ i wobec tego trójkąt $ADM$ jest równoramienny: $AM=DM.$ To oznacza, że w trójkącie prostokątnym $ADC$ punkt $M$ jest środkiem przeciwprostokątnej $AC.$

W ustalonym trójkącie $ABC$ punkty $D$ i $M$ są jego ustalonymi punktami; spodek wysokości z wierzchołka $C$ i środek boku $AC.$ Punkt $X$ leży na prostej wyznaczonej przez te dwa charakterystyczne punkty trójkąta $ABC.$ Jest to prosta, o którą chodzi w tezie zadania.

Przypuśćmy, wbrew tezie zadania, że dla pewnego $n\ge 1$ cyfry (binarne) $c_i$ o numerach $i=n,\dots ,2n$ są wszystkie zerami. Niech $$A_n=2+\sum _{i=1}^{n-1}{2}^{-i}{c}_i.$$ Dostajemy dwustronne oszacowanie: $$0<\sqrt{7}-A_n<\sum _{i=2n+1}^{\mathrm{\infty }}{2}^{-i}{c}_i\le 4^{-n}.$$ Mnożymy uzyskaną nierówność podwójną przez $\sqrt{7}+A_n,$ biorąc ponownie pod uwagę, że $A_n<\sqrt{7}$: $$0<7-A_n^2<4^{-n}(\sqrt{7}+A_n)<4^{-n}\cdot 2\sqrt{7}.$$ Po pomnożeniu jeszcze przez $4^{n-1}$ otrzymujemy $$0<4^{n-1}\cdot 7-(2^{n-1}{A}_n{)}^2<\frac{1}{2}\sqrt{7}.$$ Liczba w nawiasie jest całkowita, więc powyższa różnica musi być równa 1 (to jedyna liczba całkowita w przedziale $(0,\frac{1}{2}\sqrt{7})$). Zatem $$(2^{n-1}{A}_n{)}^2=4^{n-1}\cdot 7-1.$$ Ale kongruencja $x^2\equiv -1$ (mod 7) nie ma rozwiązań. Sprzeczność kończy dowód.

Napełnianie naczynia zachodzi szybko, można więc zaniedbać wymianę ciepła między powietrzem wchodzącym do naczynia a powietrzem atmosferycznym. Powietrze wchodzi do naczynia w postaci strumienia, którego energia kinetyczna uzyskana zostaje dzięki pracy $W$ wykonanej przez siłę parcia powietrza atmosferycznego. Energia ta zamienia się na energię chaotycznego ruchu cząsteczek powietrza w naczyniu, więc zmiana energii wewnętrznej powietrza, które dostało się do naczynia, równa jest pracy $W.$ $$\begin{array}{}\text{(1)}& \mathrm{\Delta }U=n{c}_V(T-T_0)=W,\end{array}$$ gdzie $n$ jest liczbą moli powietrza, które weszło do naczynia, a $c_V$ jego ciepłem molowym przy stałej objętości.

Aby obliczyć pracę $W,$ możemy wyobrazić sobie, że nasze opróżnione naczynie znajduje się wewnątrz wypełnionego powietrzem dużego cylindra z ruchomym tłokiem (rys. 1).

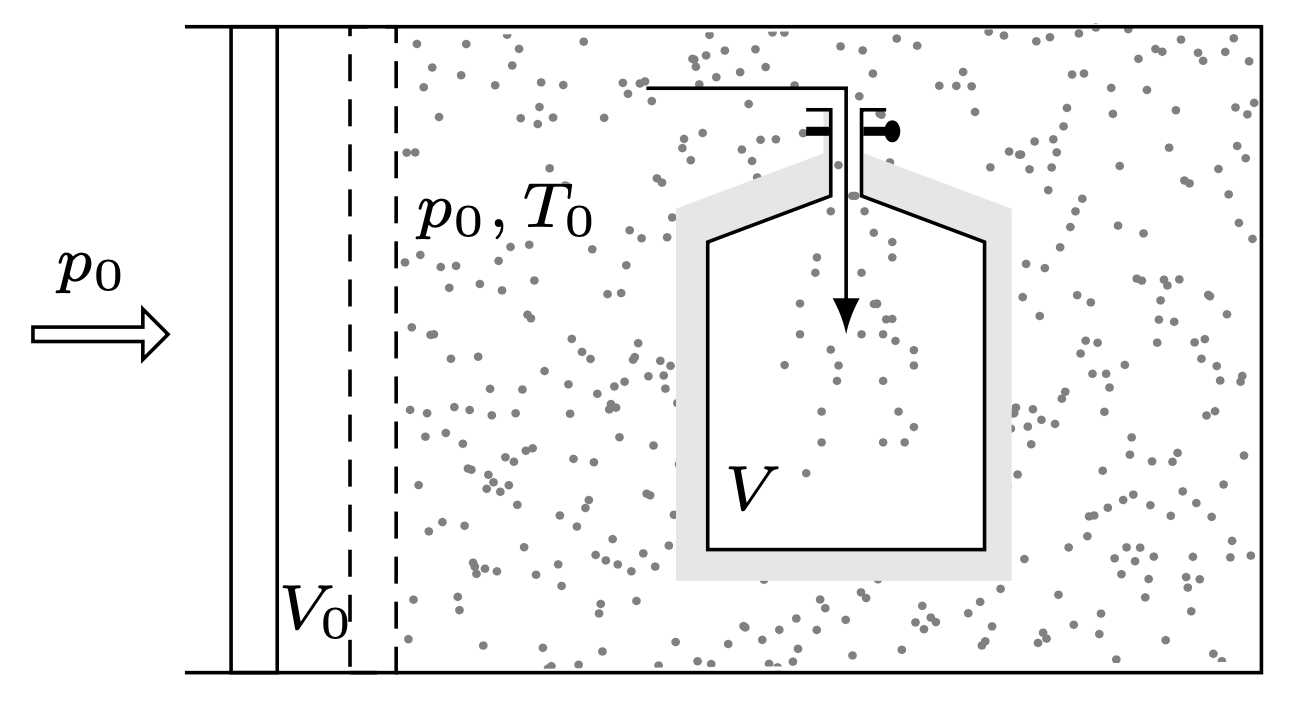
Rys. 1

Ciśnienie i temperatura wewnątrz cylindra są takie same jak w atmosferze. Procesowi napełniania naczynia towarzyszy przemieszczanie tłoka, przy zachowaniu stałego ciśnienia $p_0.$ Ponieważ do opróżnionego naczynia weszło dokładnie tyle powietrza, ile wyparł przemieszczający się tłok, możemy napisać: $$\begin{array}{}\text{(2)}& W=p_0{V}_0=nR{T}_0,\end{array}$$ gdzie $V_0$jest zmniejszeniem objętości cylindra, a $R$ stałą gazową.

Z $\text{(1)}$ i $\text{(2)}$ temperatura końcowa wyraża się zależnością: $$T=T_0(1+R/c_V)=\gamma T_0.$$ Wynik nie zależy od objętości naczynia ani od wartości ciśnienia atmosferycznego. Nie zależy też od tego, czy zapełnianie naczynia zostanie doprowadzone do końca, gdy ciśnienie w nim wyrówna się z ciśnieniem atmosferycznym, czy też naczynie zamkniemy wcześniej.

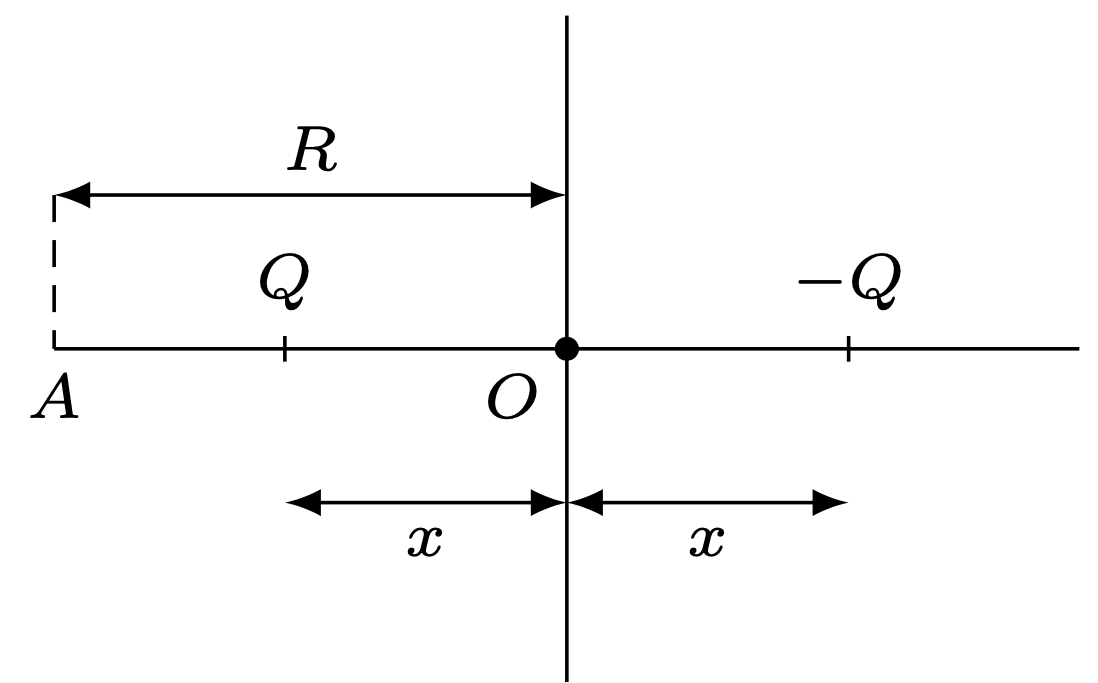
Rys. 2

W obecności cząstki naładowanej na płaszczyźnie przewodzącej pojawiają się ładunki przyciągane przez tę cząstkę. Ich działanie równoważne jest działaniu ładunku obrazu o wartości $-Q$ umieszczonego w takiej samej odległości od płaszczyzny po jej drugiej stronie.

Ponieważ zarówno siła Coulomba, jak i siła grawitacji są odwrotnie proporcjonalne do kwadratu odległości między oddziałującymi obiektami, możemy wykorzystać naszą wiedzę z grawitacji. Wprowadźmy masę $M$ umieszczoną w punkcie $O$ (rys. 2), której siła oddziaływania grawitacyjnego z cząstką o masie $m$ odległą o $x$ od punktu $O$ jest taka sama, jak siła oddziaływania kulombowskiego cząstki o ładunku $Q$ z ładunkiem obrazem: $$F=GMm/x^2=k{Q}^2/4x^2,\text{ stąd }M=k{Q}^2/4Gm.$$ Rozważmy teraz cząstkę o masie $m,$ która krąży wokół nieruchomej masy $M$ po orbicie kołowej o promieniu $R.$ Jej okres obiegu $T_0=2\pi \sqrt{R^3/GM}.$

Zmniejszając prędkość tej cząstki w punkcie $A,$ otrzymujemy tory eliptyczne, których jedno z ognisk znajduje się w punkcie $O,$ a drugie dąży do punktu $A,$ gdy prędkość początkowa cząstki dąży do zera. Ta graniczna elipsa o półosi wielkiej równej $a=R/2$ to tor cząstki o masie $m$ spadającej na masę $M.$ Zgodnie z trzecim prawem Keplera okres obiegu po tej elipsie $$T=T_0\sqrt{a^3/{a_0}^3}=T_0/2\sqrt{2},\text{ gdzie }{a}_0=R.$$ Szukany czas, po którym cząstka naładowana doleci do płaszczyzny, jest dwa razy krótszy: $$t=\frac{T}{2}=\frac{\pi R}{Q}\sqrt{\frac{Rm}{2k}}.$$