W 1875 roku Carl Johannes Thomae (1840–1921) [1] podał elementarny przykład funkcji nieciągłej w nieskończenie wielu punktach, która jest całkowalna w sensie Riemanna. Funkcja ta stała się koronnym argumentem świadczącym o wyższości całki Riemanna (1854) nad całką Cauchy’ego (1823).
Bernhard Riemann (1826–1866) w 1854 roku przedstawił Wydziałowi Filozoficznemu Uniwersytetu w Getyndze pracę habilitacyjną „Üeber die Darstellbarkeit einer Function durch eine trigonometrische Reihe” (praca została opublikowana w 1867 r., po śmierci Riemanna). W tej pracy nakreślona została koncepcja całki Riemanna, ale przykład funkcji ilustrującej jej istotę okazał się trochę skomplikowany.
Fundamentalne pytania Riemanna: Jak nieciągła może być funkcja całkowalna? – nadal czekało na odpowiedź. Dopiero po blisko pięćdziesięciu latach powstała teoria miary i całki Lebesgue’a (1902), ogólniejsza od całki Riemanna!
Oj, myślę sobie czasem od samego rana,
W czym jest całka Lebesgue’a lepsza
od Riemanna,
Głupio będzie Riemannowi,
Jak się w grobie o tym dowi.
Z „Hymnu matematyków”
(lata 60. XX wieku)
O mierze i całce Lebesgue’a pisał Michał Miśkiewicz w \(\Delta^4_{22}\).
W międzyczasie panowało przekonanie o możliwości tworzenia najdziwniejszych funkcji. Na brak przykładu funkcji ciągłej w punktach wymiernych, a nieciągłej w punktach niewymiernych odpowiadano, że to tylko kwestia czasu i właściwego pomysłu, którego teraz brakuje.
Kłam tego typu spekulacjom zadał dziewiętnastoletni Vito Volterra (1860–1940) w pracy [2], gdy był studentem Scuola Normale Superiore di Pisa.
Zanim przedstawimy obserwację Volterry, wykazaną elementarnymi środkami, popatrzmy na funkcję Thomae.
Przykład (C.J. Thomae, 1875). Niech \(f\colon\mathbb{R}\rightarrow [0,1]\) będzie funkcją opisaną wzorem \[\begin{gathered} f(x)= \begin{cases} 1 & \text{dla}~ x=0, \\ \frac{1}{q} & \text{dla}~x=\frac{p}{q},~~\text{gdzie}~p\neq 0,~q>0~\text{i~ułamek}~ \frac{p}{q}~\text{jest nieskracalny}, \\ 0 & \text{dla liczb niewymiernych}~ x. \end{cases} \end{gathered}\] Funkcja \(f\) jest ciągła dla każdej niewymiernej wartości \(x\) i jest nieciągła w każdym punkcie wymiernym \(x,\) co poniżej sprawdzimy.
Zauważmy, że \(f\) jest funkcją okresową o okresie podstawowym równym \(1.\) Ponieważ dla liczby niewymiernej \(x\) liczba \(x+1\) też jest niewymierna, więc \(f(x)=f(x+1)=0.\) Dla \(x=0,\) \(f(0)=f(1)=1.\) Gdy \(x=\frac{p}{q}\) i ułamek \(\frac{p}{q}\) jest nieskracalny, to \(x+1=\frac{p+q}{q}\) i ułamek \(\frac{p+q}{q}\) pozostaje nieskracalny. Zatem \(f(\frac{p}{q})=f(\frac{p+q}{q})=\frac{1}{q}.\)
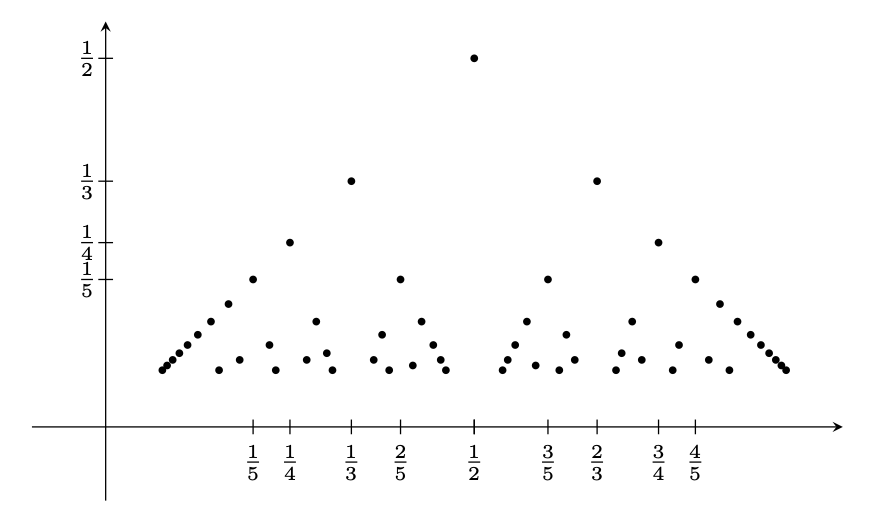
Rys. 1. Przybliżenie funkcji \(f\) w przedziale \((0,1)\)
Literatura
C.J. Thomae, „Ein Beispiel einer Function, welche in keinem Intervalle beschränkt ist, aber doch Riemann’sche Integral besitzt”, Sitzungsber, Berliner Math. Gesellschaft, 1875.
V. Volterra, „Alcune osservazioni sulle funzioni punteggiate discontinue”, Giornale di matematiche 19 (1881), 76-87.
W punkcie \(x=0\) funkcja \(f\) nie jest ciągła, bo \(f(\frac{1}{q})=\frac{1}{q}\rightarrow 0\neq 1=f(0)\) przy \(q\rightarrow\infty.\) Niech \(x_0\in (0,1).\) Dla każdego \(\varepsilon>0\) istnieje skończona liczba takich liczb naturalnych \(q,\) że \(q\leqslant\frac{1}{\varepsilon}.\) To oznacza, że w przedziale \((0,1)\) jest tylko skończenie wiele liczb wymiernych \(\frac{p}{q},\) dla których \(f(\frac{p}{q})=\frac{1}{q}\geqslant \varepsilon.\) Istnieje więc taka \(\delta >0,\) że w otoczeniu \({(x_0-\delta,x_0+\delta)}\) nie ma punktów \(x,\) dla których \(f(x)\geqslant \varepsilon\) (być może z wyjątkiem punktu \(x_0\)). Zatem dla wszystkich punktów \(x\) takich, że \(0<\vert x-x_0\vert<\delta\) mamy \(\vert f(x)\vert <\varepsilon.\) Dowolność wyboru \(\varepsilon >0\) oznacza, że \(\lim\limits_{x \to x_0} f(x) = 0\) dla każdego punktu \(x_0 \in (0,1).\)
W konsekwencji, jeśli \(x_0\) jest liczbą niewymierną, to \(f(x_0)=0,\) więc funkcja \(f\) jest w tym punkcie ciągła. Jeśli \(x_0\) jest liczbą wymierną, to \(f(x_0)\neq 0,\) więc funkcja \(f\) w tym punkcie nie jest ciągła.
Okresowość funkcji \(f\) rozciąga te własności na całą dziedzinę \(\mathbb{R}.\) \(\Box\)
Mamy więc przykład funkcji \(f\colon\mathbb{R}\rightarrow\mathbb{R},\) w której punkty ciągłości oraz punkty nieciągłości tworzą zbiory gęste, i to dość dokładnie wymieszane.
Zbiór \(A\subset \mathbb{R}\) jest gęsty, gdy każdy niepusty przedział otwarty zawiera co najmniej jeden element zbioru \(A.\)
Vito Volterra (1860–1940), Piza 1881Vito Volterra był jednym z prekursorów analizy funkcjonalnej, stworzył teorię funkcji, których argumentami są funkcje (1887). Miał znaczące osiągnięcia w teorii równań całkowych. W 1931 roku z powodu odmowy złożenia przysięgi lojalności wobec faszystowskiego rządu Benito Mussoliniego został usunięty z zajmowanych stanowisk.
Przyjmijmy następujące określenie. Funkcję \(f\colon(a,b)\rightarrow\mathbb{R}\) nazywamy punktowo nieciągłą, gdy jest nieciągła w nieskończenie wielu punktach, pozostając funkcją ciągłą na gęstym podzbiorze dziedziny.
Oto zapowiedziany rezultat odkryty przez dziewiętnastoletniego Volterrę.
Twierdzenie (V. Volterra, 1881). Nie istnieją dwie funkcje punktowo nieciągłe \(f,g\colon(a,b)\rightarrow \mathbb{R},\) dla których zbiór punktów ciągłości jednej jest zbiorem punktów nieciągłości drugiej, i vice versa.
Dla ustalonej funkcji \(f\) niech \(C_f=\{x\in (a,b): f\) jest funkcją ciągłą w \(x\},\) \(D_f=\{x\in (a,b): f~ \text{nie jest funkcją ciągłą w}~ x\}.\) Są to takie zbiory niepuste, że \(C_f\cup D_f=(a,b)\) i \(C_f\cap D_f=\emptyset.\)
Załóżmy, że \(f\) i \(g\) są takimi funkcjami punktowo nieciągłymi, że \(C_f=D_g\) i \(D_f= C_g.\) Skoro \(f\) jest funkcją punktowo nieciągłą, to istnieje punkt \(x_0,\) w którym \(f\) jest ciągła. Wtedy z definicji ciągłości funkcji w punkcie dla \(\varepsilon =\frac{1}{2}\) istnieje taka \(\delta >0,\) że przedział otwarty \((x_0-\delta,x_0+\delta)\subset (a,b)\) i jeśli \(0<\vert x - x_0\vert <\delta,\) to \(\vert f(x)-f(x_0)\vert <\frac{1}{2}.\) W przedziale \((x_0-\delta,x_0+\delta)\) wybieramy przedział domknięty \([a_1,b_1],\) \(a_1<b_1.\) Wówczas, korzystając z nierówności trójkąta, dla dowolnych \(x,y\in [a_1,b_1]\) mamy \[\vert f(x)-f(y)\vert \leqslant \vert f(x)-f(x_0)\vert +\vert f(x_0)-f(y)\vert <\frac{1}{2}+\frac{1}{2}=1.~~(1)\]
Ponieważ \(g\) też jest funkcją punktowo nieciągłą, więc w przedziale otwartym \((a_1,b_1)\) istnieje punkt \(x_1,\) w którym \(g\) jest ciągła. Stosując podaną wyżej argumentację do funkcji \(g,\) znajdujemy taki przedział domknięty \([a_1',b_1']\subset (a_1,b_1),\) że dla dowolnych \(x,y\in [a_1',b_1']\) mamy \(\vert g(x)-g(y)\vert <1.\) Łącznie z warunkiem (1), dla dowolnych \(x,y\in [a_1',b_1']\) otrzymujemy \[\vert f(x)-f(y)\vert <1 ~~\text{i}~~\vert g(x)-g(y)\vert < 1.\] Powtarzając to rozumowanie dla kolejnych wartości \(\varepsilon\) równych, odpowiednio, \(\frac{1}{2^2}, \frac{1}{2^3},\dots,\frac{1}{2^k},\dots\) otrzymujemy ciąg takich przedziałów domkniętych \[[a_1',b_1']\supset [a_2',b_2']\supset [a_3',b_3']\supset \dots,\] że jeśli \(x,y\in [a_k',b_k'],\) to \[\vert f(x)-f(y)\vert <\frac{1}{2^{k-1}}~~\text{i}~~\vert g(x)-g(y)\vert <\frac{1}{2^{k-1}}.~~(2)\] Twierdzenie Cantora (zob. margines obok) gwarantuje istnienie punktu \(c\in \bigcap\limits_{k=1}^{\infty}[a_k',b_k'].\)
Twierdzenie (G. Cantor). Niech \(\{F_k\}\) będzie ciągiem zstępującym \(F_k\supset F_{k+1}\) niepustych przedziałów domkniętych i ograniczonych na prostej euklidesowej \(\mathbb{R}.\) Wtedy \(\bigcap\limits_{k=1}^{\infty}F_k\neq\emptyset.\)
W punkcie \(c\) funkcja \(f\) jest ciągła. Istotnie, dla danego \(\varepsilon >0\) tak wybieramy liczbę naturalną \(k,\) aby \(\frac{1}{2^{k-1}}<\varepsilon.\) Ponieważ \(c\in [a_{k+1}',b_{k+1}'],\) a przedział \([a_{k+1}',b_{k+1}']\) zawarty jest w przedziale otwartym \((a_k',b_k'),\) więc istnieje taka \(\delta >0,\) że \((c-\delta,c+\delta)\subset (a_k',b_k')\subset [a_k',b_k'].\) Wtedy z warunku (2) dla dowolnego \(x\) takiego, że \(0<\vert x-c\vert <\delta,\) mamy \(\vert f(x)-f(c)\vert <\frac{1}{2^{k-1}}<\varepsilon.\) Oznacza to, że \(\lim\limits_{x\rightarrow c}f(x)=f(c),\) czyli \(f\) jest funkcją ciągłą w punkcie \(c.\) Identyczna argumentacja pokazuje, że funkcja \(g\) też jest ciągła w punkcie \(c.\) Zatem \(c\in C_f\cap C_g=C_f\cap D_f=\emptyset.\) Sprzeczność.
Przykład Thomae w połączeniu z wynikiem Volterry zapewnia następujący wniosek:
Wniosek ten można również uzyskać, rozważając zbiory \(F_{\sigma}\) i \(G_{\delta}\) (pisał o tym Jerzy Ryll w \(\Delta_{83}^8\)) lub korzystając z twierdzenia Baire’a (1899).
Wniosek. Nie istnieje funkcja \(f\colon\mathbb{R}\rightarrow\mathbb{R},\) która jest ciągła w każdym punkcie wymiernym i nieciągła w każdym punkcie niewymiernym dziedziny.
Przynajmniej w matematyce istnieją granice osobliwości!

