Uniwersytet im. A. Mickiewicza w Poznaniu
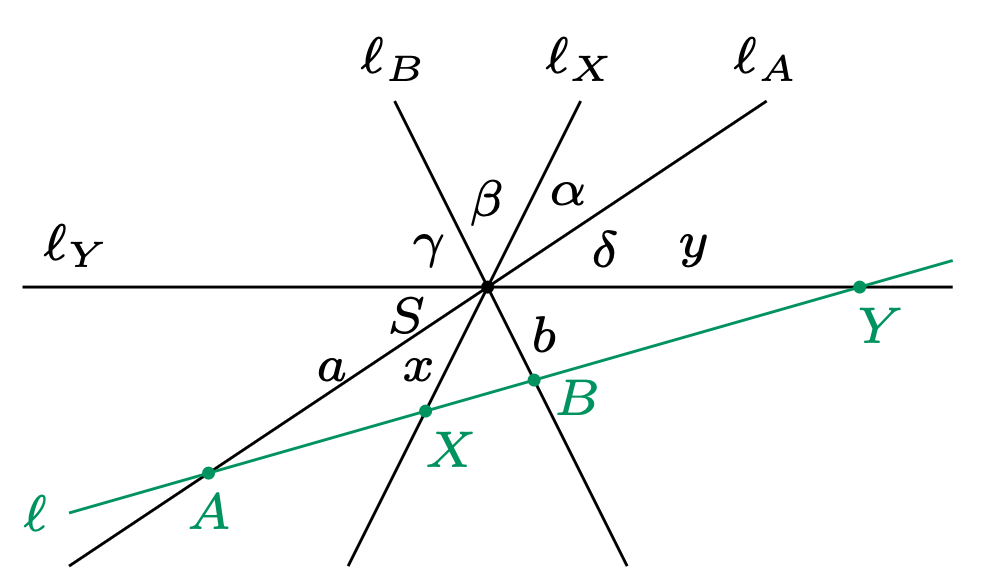
Rys. 1
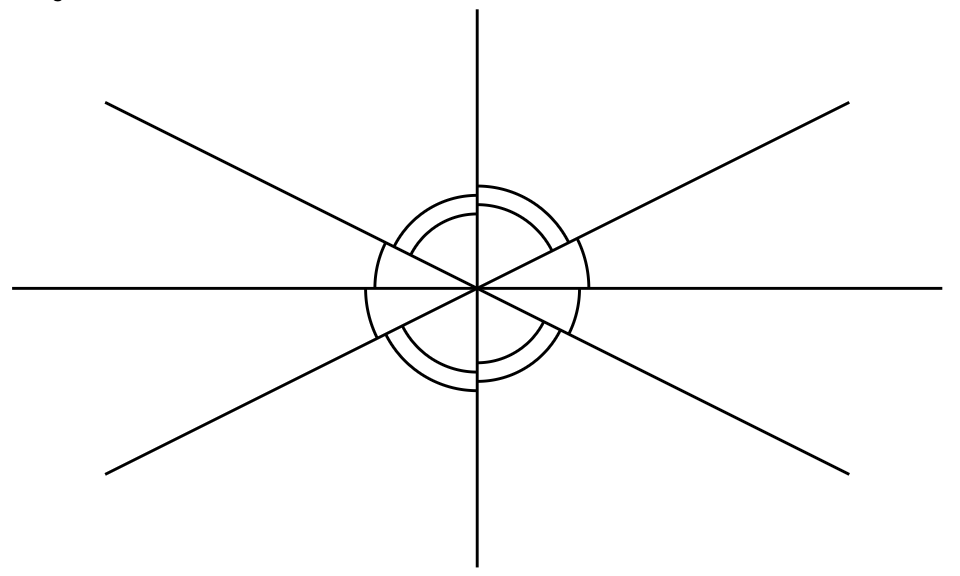
Rys. 2
Przed przystąpieniem do lektury zachęcam Czytelnika do zapoznania się z poprzednim odcinkiem.
Rozważmy konfigurację geometryczną z rysunku 1. Obliczając na dwa sposoby pola trójkątów \(AXS\) i \(BXS,\) otrzymujemy \[\frac{|AX|}{|BX|} = \frac{[AXS]}{[BXS]} = \frac{\frac12ax\sin\alpha}{\frac12bx\sin\beta}=\frac{a\sin\alpha}{b\sin\beta}.\] Analogicznie \(\frac{|AY|}{|BY|} = \frac{a\sin(\alpha+\beta+\gamma)}{b\sin\gamma} = \frac{a\sin\delta}{b\sin\gamma}.\) Mamy więc równoważność:
Odcinki \(AB\) i \(XY\) są harmonicznie sprzężone \(\iff\) \(\sin\alpha\sin\gamma = \sin\beta\sin\delta.\)
Powyższa równość nie zależy od położenia prostej \(\ell\) (nawet gdy przecina proste \(\ell_A,\) \(\ell_X,\) \(\ell_B,\) \(\ell_Y\) w innej kolejności), więc jest ona własnością pęku. Wnioskujemy zatem, że każda prosta przecinająca te cztery w punktach kolejno \(A,\) \(X,\) \(B,\) \(Y,\) sprezentuje nam harmonicznie sprzężone odcinki \(AB\) i \(XY.\) Taki pęk czterech prostych nazywamy pękiem harmonicznym, a punkt \(S\) – jego środkiem.
Rozważania te należy uzupełnić o prostą \(\ell\) równoległą do, powiedzmy, \(\ell_Y\) – wówczas \(Y=\infty.\) W tej sytuacji harmoniczne sprzężenie odcinków \(AB\) i \(XY\) jest równoważne równości \(|AX|=|BX|.\) Z równoległości \(\ell_Y\parallel\ell\) mamy \(|\measuredangle SAX|=\delta\) i \(|\measuredangle SBX|=\gamma.\) Z twierdzenia sinusów dla trójkąta \(ABS\) mamy \(a\sin \delta=b\sin \gamma,\) skąd \[\frac{|AX|}{|BX|}=\frac{a\sin\alpha}{b\sin\beta}= \frac{a\sin\alpha}{b\sin\beta}\cdot \frac{b\sin\gamma}{a\sin\delta}= \frac{\sin\alpha\sin\gamma}{\sin\beta\sin\delta}.\] Dlatego \(|AX|=|BX|\) wtedy i tylko wtedy, gdy \(\sin\alpha\sin\gamma = \sin\beta\sin\delta.\) W końcu wykazaliśmy:
Twierdzenie 1. Przecięcie pęku pewną prostą daje parę odcinków harmonicznie sprzężonych wtedy i tylko wtedy, gdy przecięcie go każdą prostą daje parę odcinków harmonicznie sprzężonych.
Na koniec jeszcze o pewnym szczególnym pęku harmonicznym. Na potrzeby kącika będę go nazywał prostokątnym (nie jest to nazwa oficjalna, ale mogłaby taką być), ponieważ pewne dwie proste należące do niego przecinają się pod kątem prostym (rys. 2). Poniższe twierdzenie szczegółowo opisuje tę konfigurację.
Twierdzenie \(\frac23.\) Dany jest trójkąt \(ABS.\) Punkty \(X\) i \(Y\) leżą na prostej \(AB.\) Jeśli spełnione są pewne dwa z poniższych warunków, to zachodzi także trzeci:
odcinki \(AB\) i \(XY\) są sprzężone harmonicznie;
kąt \(XSY\) jest prosty;
prosta \(SX\) jest dwusieczną kąta \(ASB.\)
Dowód. Załóżmy najpierw, że zachodzą warunki (b) i (c). Prosta \(SY\) jest dwusieczną kąta zewnętrznego \(ASB,\) więc odcinki \(AB\) i \(XY\) są sprzężone harmonicznie na mocy twierdzenia 2(3) z poprzedniego kącika. Załóżmy teraz, że zachodzi (a) – pokażemy, że wówczas (b) i (c) są równoważne, czym zakończymy dowód twierdzenia. Poprowadźmy prostą \(\ell'\) prostopadłą do \(SX,\) przecinającą proste \(AS,\) \(BS,\) \(XS,\) \(YS\) w punktach, odpowiednio, \(A',\) \(B',\) \(X',\) \(Y'.\) Zachodzą następujące równoważności: \[|\measuredangle XSY|=90^\circ \iff Y'=\infty \iff |X'A'|=|X'B'| \iff |\measuredangle ASX|=|\measuredangle BSX|.\]
Zadania
-
Dany jest trapez \(ABCD.\) Punkty \(P\) i \(Q\) są środkami podstaw, odpowiednio, \(AB\) i \(CD.\) Przekątne tego trapezu przecinają się w punkcie \(R,\) a przedłużenia ramion – w punkcie \(S.\) Okręgi o średnicach \(PQ\) i \(RS\) przecinają się w punktach \(K\) i \(L.\) Udowodnić, że \(|\measuredangle QKR|=45^\circ.\)
Wskazówka Odcinki \(PQ\) i \(RS\) są harmonicznie sprzężone (twierdzenie 2(1) z poprzedniego kącika). Mamy \(|\measuredangle PKQ|=|\measuredangle RKS|=90^\circ,\) więc wystarczy zastosować twierdzenie \(\frac 23.\)
-
Punkt \(X\) leży na wysokości \(AD\) trójkąta \(ABC.\) Proste \(BX\) i \(CX\) przecinają, odpowiednio, odcinki \(AC\) i \(AB\) w punktach \(E\) i \(F.\) Udowodnić, że prosta \(AD\) jest dwusieczną kąta \(EDF.\)
Wskazówka Niech prosta \(EF\) przecina proste \(BC\) i \(AD\) w punktach odpowiednio \(Y\) i \(Z.\) Odcinki \(BC\) i \(DY\) są harmonicznie sprężone (twierdzenie 2(2) z poprzedniego kącika), a więc \(EF\) i \(ZY\) również są harmonicznie sprzężone (twierdzenie 1). Teraz wystarczy zauważyć, że proste \(DF,\) \(DZ,\) \(DE,\) \(DY\) tworzą prostokątny pęk harmoniczny i zastosować twierdzenie \(\frac 23.\)
-
Okrąg wpisany w trójkąt \(ABC\) jest styczny do odcinków \(BC,\) \(CA,\) \(AB\) w punktach, odpowiednio, \(D,\) \(E,\) \(F.\) Dwusieczna kąta \(BAC\) przecina odcinek \(DE\) w punkcie \(P.\) Wykazać, że \(AP\bot BP.\)
Wskazówka Niech \(K\) będzie przecięciem prostych \(AB\) i \(DE.\) Na mocy twierdzenia Cevy odcinki \(AD,\) \(BE\) i \(CF\) przecinają się w jednym punkcie, więc \(AB\) i \(KF\) są harmonicznie sprzężone. Ponadto trójkąty \(AEP\) i \(AFP\) są przystające. Korzystając dodatkowo z twierdzenia o dwusiecznej, możemy więc napisać: \(\frac{|PF|}{|PK|} = \frac{|EP|}{|PK|} = \frac{|AE|}{|AK|} = \frac{|AF|}{|AK|} = \frac{|BF|}{|BK|}.\) Pozostaje skorzystać z twierdzenia odwrotnego do twierdzenia o dwusiecznej.
-
Dany jest okrąg \(\omega\) o średnicy \(AB.\) Punkt \(P\) leży na prostej \(AB,\) przy czym punkt \(B\) znajduje się na odcinku \(AP.\) Na okręgu \(\omega\) wybrano taki punkt \(T,\) by prosta \(PT\) była do tego okręgu styczna. Punkt \(M\) jest środkiem odcinka \(PT,\) a punkt \(N\) jest rzutem prostopadłym punktu \(T\) na odcinek \(AB.\) Proste \(NT\) i \(BM\) przecinają się w punkcie \(Q.\) Dowieść, że \(AQ\parallel PT.\)
Wskazówka Niech \(R\) będzie punktem przecięcia \(AQ\) i \(PT\) (dopuszczamy \(R=\infty\)). Odcinki \(AB\) i \(NP\) są harmonicznie sprzężone (zadanie 1(b) albo 4 z poprzedniego kącika), zatem również odcinki \(TP\) i \(MR\) są harmonicznie sprzężone – więc \(R=\infty.\)