Afiliacja: Uniwersytet w Jyväskylä
Wyobraźmy sobie, że bierzemy do ręki naszą ulubioną foremkę w kształcie Muminka i wycinamy nią pierniczek. Muminek, jak wiemy, ma dość obłe kształty (podobno ich autorka, Tove Jansson, podczas tworzenia rysunków tych postaci inspirowała się kształtem zasp śnieżnych; fińskie lasy zimą zdają się roić od Muminków). Gdybyśmy nie mieli odpowiednich foremek, a bardzo chcieli mieć pierniczek w kształcie Muminka, moglibyśmy wyciąć szklanką kółko i zdeformować je do kształtu tego sympatycznego bohatera dziecięcych opowieści. Innymi słowy, znaleźlibyśmy funkcję \(f,\) która przekształca koło (dwuwymiarową kulę) na pewien obszar (dwuwymiarowego Muminka). Możemy wykonać to przekształcenie na wiele sposobów, ale na potrzeby naszej opowieści lepiej będzie zamienić koło w Muminka w sposób dyfeomorficzny.
Dyfeomorfizm to przekształcenie o wielu cechach pożądanych z punktu widzenia analizy matematycznej: jest odwracalne (czyli istnieje przekształcenie odwrotne) oraz zarówno ono samo, jak i jego odwrotność są różniczkowalne. Przegryźmy tę definicję powoli, jakby to był ostatni pierniczek w tym roku. Żeby przekształcenie było odwracalne, każde dwa różne punkty ciasta muszą zostać przekształcone na dwa różne punkty (muminkowego) ciasta. Innymi słowy, nie wolno nam sklejać ze sobą kawałków ciasta. Wówczas będziemy mogli, po uformowaniu Muminka, wykonać ruchy odwrotne do wcześniejszych i wrócić do pierwotnego kształtu koła. Różniczkowalność to trochę trudniejsze słowo, znane licealistom przygotowującym się do matury rozszerzonej. Nie będziemy tu przytaczać definicji, spróbujemy natomiast opisać, jak wygląda takie przekształcenie, które jest różniczkowalne (i którego odwrotność również taka jest). Otóż takie przekształcenie wygląda trochę jak Muminek – jest obłe, pełne krągłości, nie przyczynia się do powstawania kantów ani szpiczastych elementów (zaokrągla, choćby delikatnie, nawet muminkowe uszy!). Biorąc to wszystko pod uwagę, możemy stwierdzić, że jeśli uformujemy Muminka z kółka poprzez rozciąganie ciasta w odpowiednich miejscach, to deformacja koła w Muminka będzie dyfeomorfizmem. Co więcej, w podobny sposób możemy przekształcić koło na kształt płaskiej Małej Mi lub płaskiego Ryjka.
Musimy uściślić jeszcze pewną cechę dyfeomorfizmów. Dyfeomorfizmy możemy podzielić na zachowujące orientację i odwracające orientację. Wyobraźmy sobie, że nasze ciastowe kółko z wierzchu pomalowane jest na różowo, a od spodu na niebiesko. Jeśli przekształcimy kółko dyfeomorficznie w Muminka tak, że przód Muminka będzie różowy, to będzie to dyfeomorfizm zachowujący orientację. Jeśli natomiast nasz dyfeomorfizm wypluje Muminka, którego przód jest niebieski, oznacza to, że mieliśmy do czynienia z dyfeomorfizmem odwracającym orientację. Zastanówcie się, proszę, jaki dyfeomorfizm wyobraziliście sobie, gdy w poprzednich akapitach zamienialiście kółko w Muminka? No właśnie – od teraz trzymajmy się jedynie dyfeomorfizmów zachowujących orientację.
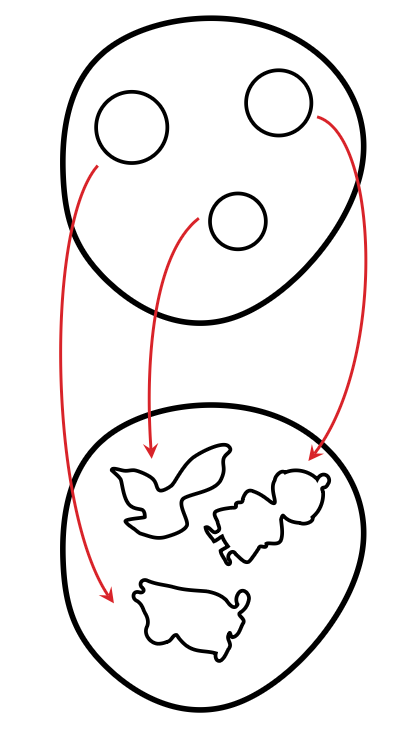
Wyobraźmy sobie dwa identyczne, okrągławe placki rozwałkowanego ciasta. Na jednym z nich zaznaczamy szklanką trzy nieprzecinające się kółka, a na drugim odciskamy foremką kształty Muminka, Małej Mi i Ryjka (które się również nie przecinają). Wiemy, że każde kolejne kółko możemy przekształcić dyfeomorfizmem na odpowiedni kształt. A czy znajdziemy dyfeomorfizm przekształcający cały lewy placek ciasta na prawy placek ciasta tak, aby wszystkie trzy kółka zostały jednocześnie przekształcone na odpowiadające im kształty? Dorzućmy do tego jeszcze jeden warunek: szukamy takiego dyfeomorfizmu, który nie będzie od nas wymagał ruszania ciasta w okolicy brzegu naszego ciastowego placka.
Ci z nas, którzy nie mają pod ręką rozwałkowanego ciasta ani foremek do pierniczków, muszą wytężyć swoją wyobraźnię: Czy na moim wyimaginowanym stole uda się tak porozciągać to ciasto, żeby powstały trzy żądane kształty jednocześnie? I to tak, żeby nie rozciągać ciasta przy brzegu? Czy udałoby się to na takim prawdziwym, kuchennym stole, na którym wycinamy pierniczki z mąki, masła i miodu? Nie wiem. Ale na wyimaginowanym stole w mojej lub Twojej głowie się uda.
Sformułujmy to pytanie trochę precyzyjniej, bo używając Muminka, Małej Mi i Ryjka, daleko nie zajedziemy. Nasz placek rozwałkowanego ciasta symbolizuje zbiór otwarty \(U\) (który jest podzbiorem płaszczyzny); kółka to będą zbiory \(D_i\) (w naszym przykładzie \(i = 1,2,3\)), a kształty Muminka, Małej Mi i Ryjka oznaczymy \(D'_ i\) (\(i = 1,2,3\)). Zbiory \(D_i\) są parami rozłączne, zbiory \(D'_i\) są parami rozłączne, ale może się zdarzyć tak, że jakiś zbiór \(D_i\) przetnie jakiś zbiór \(D'_j.\) Niech \(F_i\) będzie dyfeomorfizmem przekształcającym \(D_i\) na \(D'_i.\) Przypominam, że ustaliliśmy już, że umiemy skonstruować każdy z tych dyfeomorfizmów, przekształcający jedno konkretne kółko na jeden konkretny kształt. Naszym zadaniem jest znalezienie dyfeomorfizmu \(F\) przekształcającego \(U\) na \(U,\) o następujących własnościach:
\(F = F_i\) na \(D_i\) (czyli \(F\) pokrywa się z już znalezionymi dyfeomorfizmami \(F_i\) na każdym z kółek \(D_i\)),
\(F(x) = x\) w okolicy brzegu \(U\) (czyli dyfeomorfizm \(F\) nic nie zmienia na pewnym cienkim pasku wokół brzegu placka \(U,\) zatem jest tam identycznością).
W znalezieniu powyższego dyfeomorfizmu \(F\) są dwie trudności. Po pierwsze taki dyfeomorfizm będzie przedłużeniem każdego z dyfeomorfizmów \(F_i.\) Przedłużenie dyfeomorfizmu \(F_i\) oznacza nowy dyfeomorfizm, określony na trochę większym kółku (niż to kółko, na którym określiliśmy \(F_i\)), który pokrywa się z \(F_i\) na wyjściowym kółku. Wracając do naszej pierniczkowej metafory, powiemy, że chodzi o znalezienie deformacji, która w dokładnie ten sam sposób rozciąga ciasto w muminkowy kształt na wyjściowym kółku oraz kontynuuje rozciąganie tego ciasta poza granicami wyjściowego kółka. Co ważne, chcemy kontynuować rozciąganie tego ciasta w sposób dyfeomorficzny! Znajdowanie przedłużeń dyfeomorfizmów nie jest zadaniem łatwym. Co więcej, są dyfeomorfizmy, których nie da się przedłużyć, choćbyśmy nie wiem jak bardzo tupali nóżką. Dlatego też będziemy zakładać, że wszystkie nasze dyfeomorfizmy \(F_i\) da się rozszerzyć chociaż troszeczkę (na odrobinę większe koło).
Ktoś mógłby się zaśmiać, ha ha, niezły profesjonalizm w tej branży: zauważacie, że może wystąpić jakiś poważny problem, więc mówicie: załóżmy, że w naszym wypadku tenże problem nie wystąpi! Nie ma się co śmiać – takie myślenie jest w matematyce na porządku dziennym (nie należy jednak przykładać go do, chociażby, chodzenia samemu po zamarzniętym jeziorze. Kruchej tafli lodu nie interesuje to, że założyliśmy, że jest nie krucha, lecz gruba i wytrzymała). Zresztą, to nie jest tak, że dowodzimy nasze twierdzenie poprzez założenie tezy: zakładamy jedynie, że \(F_i\) da się trochę przedłużyć; wciąż pozostaje pytanie, jak przedłużyć je bardziej niż trochę. Wciąż pozostaje też druga trudność, którą teraz opiszemy. Musimy znaleźć sposób, żeby posklejać znalezione przedłużenia w jeden dyfeomorfizm. To sklejanie jest o tyle trudne, że musimy wymyślić, jak wygląda klej, którym sklejamy nasze dyfeomorfizmy. Brzmi to dość dramatycznie, ale o co chodzi?
Wyobraźmy sobie, że mamy nasze (już trochę przedłużone) dyfeomorfizmy \(F_i,\) i widzimy (z lewej) jedynie te kawałki ciasta, na których \(F_i\) są określone, oraz (z prawej) kawałki ciasta przekształcone przez poszczególne \(F_i.\) Po obu stronach widzimy też cienkie brzegi naszych ciastowych placków, których dyfeomorfizm \(F\) ma nie ruszać. Zarówno po lewej, jak i po prawej stronie spomiędzy kawałków ciasta wyziera kuchenny blat. Niestety do rozwiązania naszego zadania nie wystarczy to, że weźmiemy do ręki trochę ciasta i zakleimy nim blat kuchenny po lewej i prawej stronie. Musimy znaleźć dyfeomorfizm określony na doklejonym cieście po lewej stronie, który przekształca to ciasto na doklejone ciasto po prawej stronie. Co więcej, ten sklejający dyfeomorfizm musi się pokrywać z \(F_i\) w okolicy brzegu każdej z dziedzin \(F_i.\) Mam nadzieję, że znalezienie tego sklejającego dyfeomorfizmu nie wydaje się łatwym zadaniem – bo nim nie jest! Chyba że… Chyba że \(F_i (x) = x\) blisko brzegów przedłużeń swoich dziedzin! W takiej sytuacji znalezienie sklejającego dyfeomorfizmu jest bajecznie proste: będzie to dobrze nam już znany dyfeomorfizm-leniuszek, który nic nie robi, czyli identyczność.
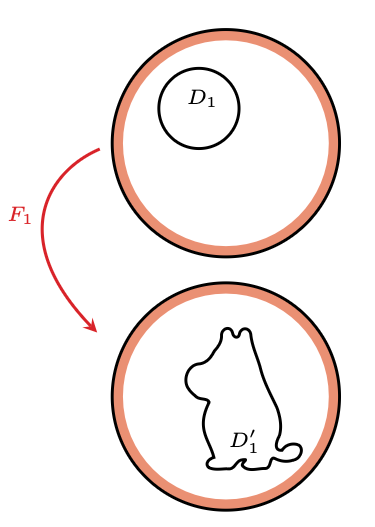
Dyfeomorfizm \(F_1\) przekształca \(D_1\) na \(D_1'\); szukamy jego przedłużenia, które jest identycznością na zaznaczonym na kolorowo obszarze
Wracamy zatem do problemu numer jeden: przedłużania dyfeomorfizmów \(F_i.\) Chcemy przedłużyć każdy z \(F_i\) w taki sposób, żeby to przedłużenie spełniało \(F_i(x) = x\) poza pewnym małym otoczeniem swojej wyjściowej dziedziny (oraz swojego oryginalnego obrazu). Innymi słowy, chcemy, żeby \(F_i\) było tam identycznością. I to, na szczęście dla naszej historii, da się zrobić – pokazał to Richard Palais, amerykański matematyk, w swojej pracy z 1960 roku (dla zainteresowanych podaję tytuł: Extending diffeomorphisms). Konstrukcja Palais jest jak zorza polarna: trzeba się trochę napracować, żeby ją zobaczyć (np. pojechać w nocy rowerem poza miasto), jest piękna i gdy się na nią patrzy, nie ma się pojęcia, skąd się wzięła. Podkreślam, że trzeba się napracować tylko trochę, bo dowód Palais może być zrozumiały dla zmotywowanego studenta drugiego roku matematyki, jest to elementarna konstrukcja używająca de facto jedynie definicji dyfeomorfizmu i różniczkowalności.
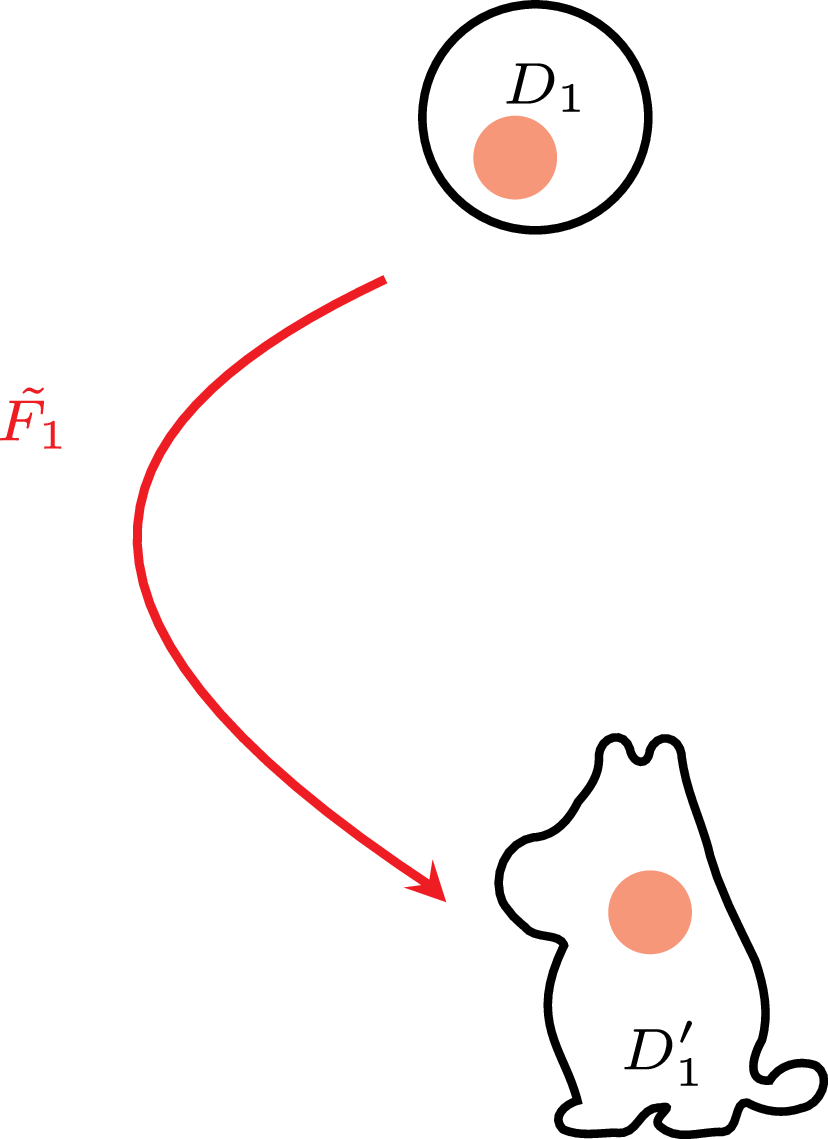
Występująca w dowodzie Palaisa modyfikacja \(\tilde{F}_i\) dyfeomorfizmu \(F_i\) jest przesunięciem na pewnej małej kulce (zaznaczonej kolorem) wewnątrz swojej dziedziny
Właśnie w elementarności tkwi piękno tego dowodu. A dlaczego jest tak zaskakująca? Palais konstruuje swoje przedłużenie w następujący sposób. Najpierw modyfikuje dyfeomorfizm \(F_i,\) nie zmieniając jego wartości przy brzegu swojej dziedziny, tak żeby ten zmodyfikowany dyfeomorfizm był zwykłym przesunięciem na pewnym małym kółku wewnątrz dziedziny. To da się zrobić, proszę mi wierzyć (wtajemniczony Czytelnik może zauważyć, że tu właśnie korzystamy z naszej umowy na dyfeomorfizmy zachowujące orientację). Używając tej modyfikacji, Palais pokazuje, jak skonstruować żądane przez nas przedłużenie, które jest identycznością poza pewnym otoczeniem swojej wyjściowej dziedziny (i swojego oryginalnego obrazu). Powtórzę to raz jeszcze, dla tych, którym szczęki jeszcze nie opadły ze zdumienia: konstruujemy przedłużenie – coś, co intuicyjnie dotyczy wartości przekształcenia przy brzegu – za pomocą przekształcenia, które ma żądane przez nas wartości wewnątrz swojej dziedziny! Za pomocą tej sztuczki możemy skonstruować odpowiednie przedłużenia dyfeomorfizmów \(F_i,\) które dają się łatwo posklejać. To sklejenie, szukany dyfeomorfizm \(F,\) będzie również spełniało warunek \(F(x) = x\) przy brzegu \(U\) (czyli \(F\) będzie identycznością przy brzegu \(U\)). W ten sposób udało nam się odpowiedzieć na nasze jakże praktyczne pierniczkowe pytanie: jest to teoretycznie możliwe, żeby dyfeomorficznie porozciągać rozwałkowane ciasto w ten sposób, żeby za jednym razem utworzyć z trzech kółek Muminka, Małą Mi i Ryjka!
No dobrze, jeszcze zastanówmy się, po co to wszystko. Te dziwne przekształcenia, to sklejanie. Mogłabym podać ileś przykładów innych matematycznych problemów, w których takie konstrukcje się przydają. Ale chyba najuczciwiej byłoby powiedzieć, że to po prostu trochę jak z pierniczkami. Piekę je, bo lubię je jeść. Wszystkich zaciekawionych (lub nieprzekonanych moimi nieprecyzyjnymi argumentami) zachęcam do lektury pracy Gluing diffeomorphisms, bi-Lipschitz mappings and homeomorphisms, w której w doborowym towarzystwie Pawła Goldsteina (z Uniwersytetu Warszawskiego) i Piotra Hajłasza (z Uniwersytetu w Pittsburghu) wyjaśniamy zawiłości tej konstrukcji i używamy jej do konstruowania innych pierniczkowych ekscesów.