Afiliacja: Nauczyciel, Warszawa
Nieczęsto zdarza się, żeby zadanie z Międzynarodowej Olimpiady Matematycznej (International Mathematical Olympiad, IMO) było dostępne dla ucznia szkoły podstawowej. Mamy na myśli coś, co da się wyjaśnić w ciągu, powiedzmy, jednego kółka matematycznego, bez konieczności wprowadzania trudnych pojęć, twierdzeń czy zaawansowanych narzędzi. Tym bardziej cieszą nas takie właśnie zadania, a jedno z nich pojawiło się nie tak dawno, bo w roku 2020. Przytoczmy (dość długą) treść w oryginalnym brzmieniu.
IMO 2020, zadanie 4. Dana jest liczba całkowita \(n > 1.\) Na zboczu góry znajduje się \(n^2\) stacji kolejki linowej, każda na innej wysokości. Każda z dwóch firm obsługujących kolejkę, \(A\) i \(B,\) posiada dokładnie \(k\) wyciągów; każdy z nich umożliwia bezpośredni przejazd z jednej ze stacji na pewną stację położoną wyżej (bez zatrzymywania się po drodze). Wszystkie \(k\) wyciągów firmy \(A\) mają \(k\) różnych stacji początkowych oraz \(k\) różnych stacji końcowych, a ponadto jeśli jeden wyciąg rozpoczyna trasę wyżej od pewnego innego, to również kończy trasę wyżej od niego. Te same warunki są spełnione przez połączenia obsługiwane przez firmę \(B.\) Powiemy, że dwie stacje są połączone przez firmę, jeśli rozpoczynając ze stacji położonej niżej, można dojechać do stacji położonej wyżej, z użyciem wyłącznie połączeń (jednego lub więcej) obsługiwanych przez tę firmę (żadne inne sposoby przemieszczania się pomiędzy stacjami kolejki nie są dozwolone).
Przyznajmy uczciwie, że połowa uczestników tych zawodów otrzymała maksymalną ocenę za to zadanie.
Wyznaczyć najmniejszą dodatnią liczbę całkowitą \(k,\) dla której z całą pewnością (niezależnie od układu połączeń) istnieje para stacji połączonych przez obydwie firmy.
Graf, jaki jest, każdy widzi. Pisaliśmy o nich już nie raz, np. w \(\Delta^{3}_{11}\), \(\Delta^{8}_{24}\) czy \(\Delta^{4}_{25}\).
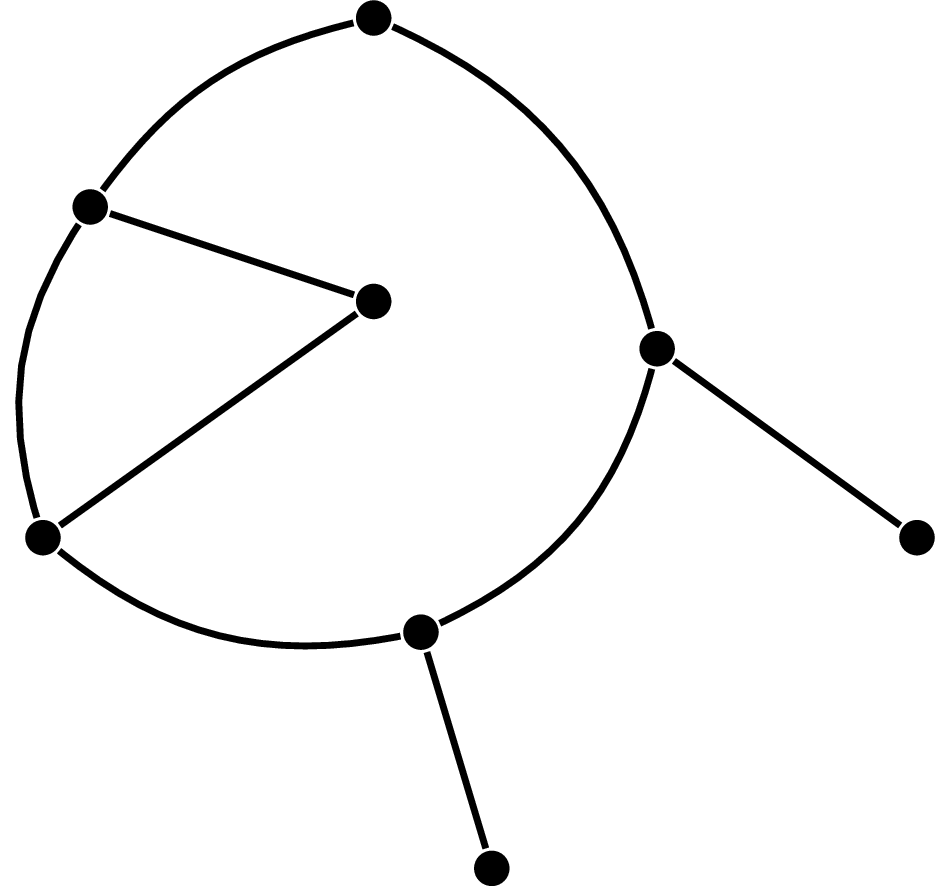
Dla matematyka jest czymś naturalnym przetłumaczenie treści tego zadania na język teorii grafów. Przy tym będziemy używać jedynie najprostszych jej pojęć. Graf jest strukturą złożoną z dwóch rodzajów elementów. Pierwszym z nich są wierzchołki, a drugim krawędzie, które stanowią połączenia między tymi pierwszymi. Każda krawędź łączy dwa wierzchołki, zwane jej końcami. Jest jasne, że taka struktura nadaje się do modelowania różnych rodzajów sieci, również tej niemal jawnie opisanej w zadaniu, złożonej ze stacji połączonych wyciągami.
Do rozwiązania naszego problemu użyjemy nie jednego, lecz dwóch grafów, \(A\) i \(B\) – po jednym dla każdej z dwóch firm. Wierzchołkami każdego z nich będą stacje kolejki linowej, natomiast krawędziami – wyciągi odpowiedniej firmy.
W danym grafie zbiór wierzchołków, które są między sobą połączone bezpośrednio lub pośrednio, nazywa się spójną składową lub po prostu składową tego grafu. Naszym celem jest więc pokazanie, że przy założeniach zadania i dla odpowiednio dużej liczby \(k\) pewne dwa wierzchołki należą do tej samej składowej grafu \(A\) oraz tej samej składowej grafu \(B.\) Korzystnie byłoby więc, gdyby w którymś z tych grafów zaistniała duża składowa (będzie wiele par stacji do wyboru), a w drugim składowych było niewiele (żeby dana para miała duże szanse znaleźć się w tej samej). Podany poniżej lemat jest sercem rozwiązania.
Lemat 1. Jeśli każdy z grafów \(A\) i \(B\) ma mniej niż \(n\) składowych, to pewne dwa wierzchołki należą do tej samej składowej grafu \(A\) oraz tej samej składowej grafu \(B.\)
Dwukrotnie objawia się tu zasada szufladkowa Dirichleta. Ten bardzo intuicyjny fakt głosi, że jeśli w \(s\) szufladach znajduje się łącznie \(p\) piłeczek, to w którejś szufladzie znajduje się ich co najmniej \(\frac{p}{s}.\) O zasadzie szufladkowej pisaliśmy na przykład w \(\Delta^{2}_{95}\) i \(\Delta^{9}_{18}\).
Dowód. Ponieważ graf \(A\) ma \(n^2\) wierzchołków podzielonych między mniej niż \(n\) składowych, więc któraś z jego składowych zawiera więcej niż \(n\) wierzchołków. W szczególności składowa ta ma więcej wierzchołków, niż istnieje składowych grafu \(B.\) Zatem pewne dwa z nich należą do tej samej składowej grafu \(B,\) spełniając tym samym warunki lematu. \(\square\)
Lemat 1 można udowodnić, stosując zasadę szufladkową tylko raz. Pozostawiamy to jako ćwiczenie dla Czytelnika Upraszczającego.
Być może większa część rozwiązania właśnie się dokonała. Pozostało jedynie określić, jak wielu wyciągów potrzeba, aby zagwarantować połączenie istniejących stacji w mniej niż \(n\) składowych.
Ponieważ stacje kolejki – wierzchołki grafów – położone są na różnych wysokościach, możemy ponumerować je liczbami naturalnymi \(1, 2, 3, \dots , n^2,\) od położonej najniżej do położonej najwyżej.
Lemat 2. Rozważamy wybrany z grafów \(A,\) \(B.\) Każda składowa tego grafu jest ścieżką, która nie zawraca. Ściślej, jeśli do pewnej składowej należą wierzchołki \(i_1 < i_2 < i_3 < \dots < i_t,\) to jedyne krawędzie tej składowej są postaci \(i_mi_{m+1}.\)
Dowód. Z definicji spójnej składowej wynika wprost, że żadna z tych stacji nie może być połączona z żadną spoza tej listy. Z drugiej strony, dana stacja może być połączona bezpośrednio tylko z jedną wyższą od siebie i jedną od siebie niższą; istotnie, połączenie \(a\) i \(b\) z \(c,\) gdzie \(a<b<c,\) przeczyłoby założeniu, że wyższy start oznacza wyższy koniec; analogicznie dla \(a>b>c.\) Zatem jeśli połączone są stacje \(i<j,\) a także \(j\) z \(l,\) to musi zachodzić \(j<l.\) Rozumując tak dalej, dostajemy dowód naszej obserwacji. \(\square\)
W szczególności żaden z grafów \(A, B\) nie zawiera cyklu. Możemy teraz powiązać liczbę \(k\) z liczbą składowych grafu, a więc z lematem 1.
Lemat 3. Graf bez cykli o \(N\) wierzchołkach i \(k\) krawędziach ma dokładnie \(N-k\) składowych.
Dowód. Skonstruujemy nasz graf, zaczynając od \(k=0\) i dodając krawędzie jedna po drugiej, w dowolnej kolejności. Oczywiście dla \(k=0\) każdy wierzchołek jest sam w swojej składowej, więc składowych jest \(N.\) Dodając nową krawędź (na dowolnym etapie konstrukcji), nie możemy połączyć nią pary wierzchołków należących do jednej składowej – wówczas powstałby cykl. Oznacza to, że każda dodawana przez nas krawędź łączy wierzchołki, które uprzednio należały do dwóch różnych składowych. Tym samym łączy ona te dwie składowe, zmniejszając łączną ich liczbę o 1. Dowód jest zakończony. \(\square\)
Jesteśmy już bardzo blisko rozwiązania. Z lematu 3 wynika, że dla \(k=n^2-n+1\) każdy z grafów \(A,\) \(B\) ma dokładnie \(n-1\) składowych, a wówczas na mocy lematu 1 istnieje para wierzchołków połączona przez każdą z dwóch firm. Bingo!
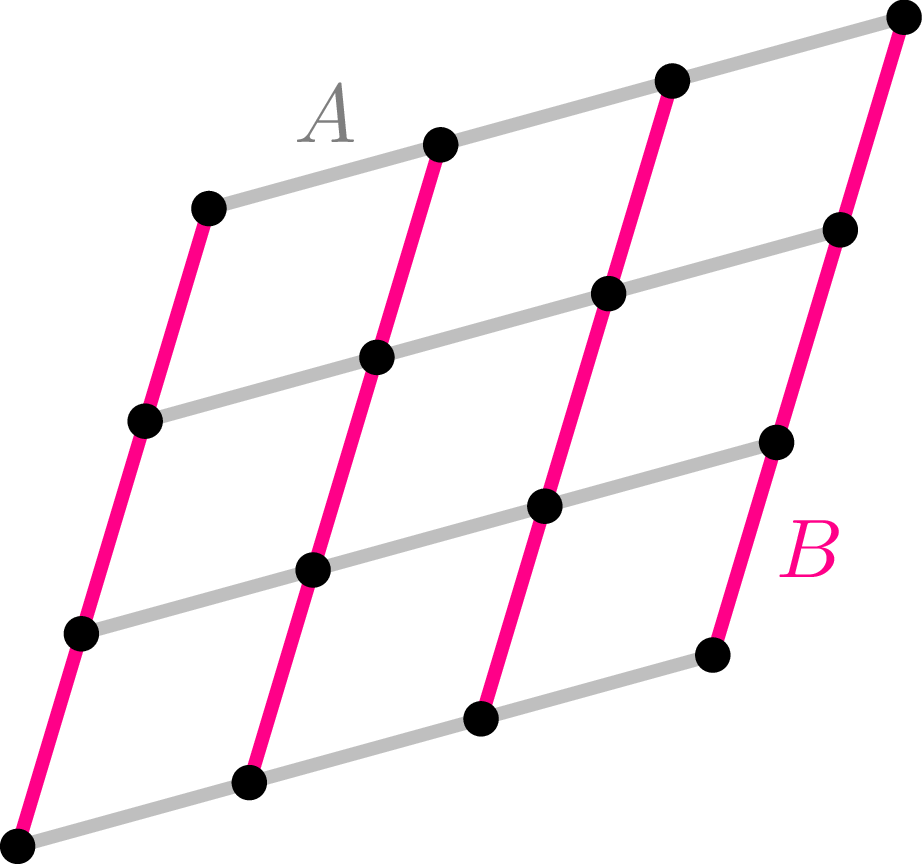
Pozostaje jeszcze jeden istotny szczegół. Czy jest to rzeczywiście minimalne \(k\)? Innymi słowy, czy może zdarzyć się, że dwóch stacji o żądanej własności nie znajdziemy przy \(k=n^2-n\)? Za odpowiedź niech posłuży schemat przedstawiony na marginesie (każdy kolor odpowiada połączeniom innej firmy).
Warto pokazywać uczniom zadania takie, jak to – wymagające, a jednak dostępne. Może nawet się zdarzyć, że zostanie rozwiązane przez samych uczniów. Ważne jest jednak, by nie zdradzać zbyt wcześnie jego źródła, aby problem nie został z góry uznany za niemożliwy do rozwiązania. Właściwie rozegrany, taki fortel może niejednej młodej osobie pokazać, jak wiele jest w jej zasięgu.