Afiliacja: Wydział Matematyki i Informatyki UJ
W artykule O obwodach poliomin (zob. \(\Delta^8_{22}\)) wyprowadziliśmy jawny wzór na minimalny obwód kształtu ułożonego z \(n\) kwadratowych kafelków (kwadratów jednostkowych), wynoszący \(2\left\lceil 2\sqrt{n}\right\rceil.\) Zapowiedzieliśmy wówczas, że po tym łagodnym wprowadzeniu w metody szacowania obwodów zmierzymy się z bardziej skomplikowanym przypadkiem kafelków trójkątnych. Słowa dotrzymujemy i zapraszamy do lektury.
Zapis \(\left\lceil x\right\rceil\) oznacza najmniejszą liczbę całkowitą nie mniejszą od \(x,\) czyli \(\left\lceil x\right\rceil-1<x\leq\left\lceil x\right\rceil.\) Wartość \(\left\lceil x\right\rceil\) nazywa się czasem sufitem liczby \(x.\)
Na początku wypadałoby jeszcze wyjaśnić pochodzenie obecnego w tytule terminu „poliapez”. Figury złożone z trójkątów równobocznych zwykło nazywać się „poliamondami”, ponieważ po angielsku dwa trójkąty tworzą „di-amond” (karo, \(\diamondsuit\)). Skoro jednak „diament” nie jest w Polsce zwyczajową nazwą rombu, możemy nazywać konfiguracje trójkątów „poliapezami”, ponieważ trzy tworzą „tr(i)-apez”.
Kształty ułożone z 1–5 trójkątów równobocznych, czyli
monapez, diapez, triapez, 3 tetrapezy
i 4 pentapezy
Początkowe wartości ciągu minimalnych obwodów odpowiadających kolejnym liczbom trójkątnych kafelków wynoszą: \(3, 4, 5, 6, 7\) i znowu \(6\) – z sześciu trójkątów możemy ułożyć sześciokąt foremny. Oczywiście dla tak małej liczby pól można ręcznie sprawdzać wszystkie układy, ale i tak warto się zastanowić, dlaczego „nagle” obwód się zmniejsza. Albo inaczej: czy minimalny obwód \(7\) dla pięciu pól można wyznaczyć prościej? Można: z układem kafelków skojarzmy graf odpowiadający temu, które pola posiadają wspólny bok. Zauważmy, że najkrótszy cykl, jaki może w takim grafie wystąpić, ma długość \(6,\) ponieważ zawsze skręcamy o \(60^\circ\) i potrzebujemy co najmniej \(6\) takich zakrętów, aby wykonać pełne okrążenie. Stąd pięć kafelków nie tworzy cyklu, a to prowadzi do wniosku, że krawędzi w grafie jest co najwyżej \(k\leq n-1=4.\) Obwód wynosi zatem co najmniej \(3n-2k\geq 15-8=7\) (od liczby wszystkich boków trójkątów odejmujemy krawędzie styku).
Na siatce kwadratowej mieliśmy bardzo użyteczne pojęcie wypukłości, które jednak nie przekłada się bezpośrednio na siatkę trójkątną. Łatwiej uogólnić „prostokąt ograniczający” – przecięcie najwęższego poziomego i pionowego pasa obejmującego poliomino. Na siatce trójkątnej musimy przeciąć trzy najwęższe pasy, równoległe do odpowiednich linii siatki i zawierające dany poliapez. W pierwszym odruchu można by nazwać taką otoczkę „sześciokątem ograniczającym” poliapez, ale liczba boków powstałej figury może być mniejsza od 6! Będziemy zatem używali określenia uwypuklenie poliapezu.
Zaznaczmy w tym miejscu, że dla uproszczenia zapisu w dalszych rozważaniach długości w kierunkach siatki mierzone będą długościami boków jej „oczek” (tzn. najmniejszych tworzonych przez nią trójkątów równobocznych), zaś długości w kierunkach prostopadłych do linii siatki (szerokości pasów) mierzymy wysokościami „oczek”. Oczywiście jednostką pola powierzchni będzie pole pojedynczego „oczka” siatki.
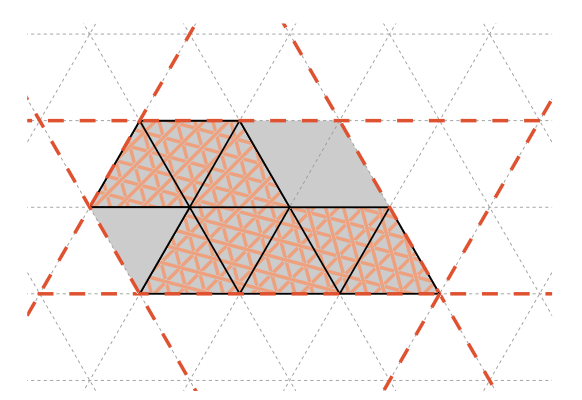
Przykładowy poliapez (oktapez) oraz jego uwypuklenie. Przerywane linie oznaczają brzegi minimalnych pasów. Zgodnie z przedstawioną w tekście konwencją ten poliapez ma obwód 10, pole 8, a ograniczają go pasy o szerokościach 2, 4 i 3.
Pokażemy teraz, że, podobnie jak dla kwadratowych kafelków, obwód poliapezu jest ograniczony z dołu przez obwód jego uwypuklenia (na siatce kwadratowej było to prawdą dla prostokąta ograniczającego). Bez straty ogólności załóżmy, że badana figura jest spójna, tzn. że żaden rząd nie jest pusty. Jest bowiem jasne, że minimalizując obwód, niczego nie tracimy, gdy stykamy ze sobą spójne składowe figury. Tym razem mamy jednak trzy kierunki wierszy/kolumn (rzędów). Rozważmy więc promienie wychodzące z każdej jednostkowej krawędzi uwypuklenia do jego wnętrza, w obu dostępnych kierunkach (trzeci jest równoległy do krawędzi). W daną krawędź wyjściowego poliapezu mogą trafić co najwyżej dwa promienie (zakładamy, że jest on nieprzezroczysty dla promieni), a liczba promieni to dwukrotność obwodu uwypuklenia. Stąd liczba wszystkich krawędzi nie może być mniejsza od wspomnianego obwodu. Zauważmy, że dla krawędzi poliapezu leżących na obwodzie jego uwypuklenia oba promienie zaczynają się i kończą w tym samym punkcie.
Rząd w poliapezie to jego część wspólna z pasem o szerokości 1, w dowolnym z trzech kierunków.
Czytelnik Obeznany z Geometrycznym Pojęciem Wypukłości może wykazać, że poliapez jest wypukłym podzbiorem płaszczyzny wtedy i tylko wtedy, gdy jest równy swojemu uwypukleniu. Warto zaznaczyć, że uwypuklenie nie jest w ogólności tożsame z klasyczną otoczką wypukłą.
Kolejny istotny fakt to stwierdzenie, że figura maksymalizująca pole przy danym obwodzie musi być wypukła (równa swojemu uwypukleniu), ponieważ w przeciwnym wypadku moglibyśmy ją uwypuklić, nie zwiększając obwodu. Formalnie ktoś mógłby zapytać: czy jeśli obwód się zmniejszy, to czy czegoś nie zepsujemy. Minimalny obwód nie jest przecież rosnącą funkcją liczby pól, więc może maksymalne pole nie musi rosnąć wraz z obwodem? Otóż okazuje się, że w tę drugą stronę zależność musi być rosnąca, ponieważ zawsze możemy dostawić jeden kafelek w taki sposób, aby zarówno pole, jak i obwód wzrosły o 1. Potencjalny spadek długości obwodu po uwypukleniu można zatem „odrobić” przy dalszym powiększaniu figury.
Kto uważa, że to zwiększanie obwodu o 1 nie jest oczywiste, ma nie tylko rację, ale i ćwiczenie do rozwiązania!
Teraz zastanówmy się, jak duże pole może mieć poliapez o danym obwodzie. Niech \(P_\triangleleft(l)\) będzie maksymalnym polem poliapezu o danym obwodzie \(l\geq 3.\) Takie maksymalne pole będzie dla nas dobrym punktem odniesienia w kontekście wyjściowego problemu, gdyż jeśli przez \(O_\triangleleft(n)\) oznaczymy minimalny obwód poliapezu o polu \(n\geq 1,\) to zachodzi \(O_\triangleleft(P_\triangleleft(l))=l,\) co teraz pokażemy. Ustalmy \(l\geq 3\) i niech \(S\) będzie wypukłym poliapezem o obwodzie \(l\) i polu \(P_\triangleleft(l).\) Gdyby istniał poliapez o obwodzie \(l'<l\) i polu \(P_\triangleleft(l),\) to jego uwypuklenie \(S'\) miałoby obwód mniejszy niż \(l\) i pole co najmniej \(P_\triangleleft(l).\) Do wypukłego poliapezu zawsze można dodać nowy rząd, zwiększając jego obwód o \(1.\) Pozwala to powiększyć \(S'\) do obwodu \(l,\) zwiększając przy tym jego pole ponad wartość \(P_\triangleleft(l)\) – uzyskujemy więc sprzeczność. Oznacza to, że faktycznie musi zachodzić \(O_\triangleleft(P_\triangleleft(l))=l.\)
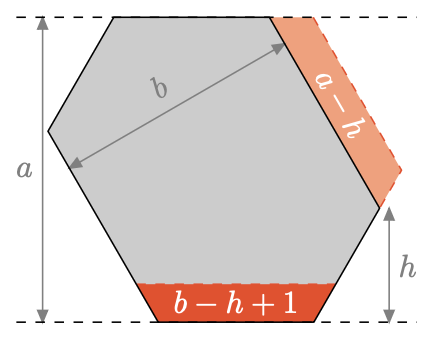
Ważną własnością takich maksymalnych poliapezów jest fakt, że ich szerokości (chodzi o szerokości trzech pasów, których przecięciem jest dany poliapez) nie mogą się różnić o więcej niż jeden. Gdyby bowiem wypukły poliapez miał szerokości \(a\geq c\geq b\) oraz \(a\geq b+2,\) to wówczas można by stworzyć poliapez o szerokościach \((a-1,c,b+1),\) który będzie miał większe pole, przy identycznym obwodzie: do tej konstrukcji wystarczy odciąć jeden rząd przy brzegu pasa o szerokości \(a\) oraz dołożyć rząd przy krawędzi pasa o szerokości \(b.\) Dalej, ponieważ \(a-1>b,\) to można tak dobrać krawędzie pasów, aby się nie spotykały nawet po odcięciu (nachodzenie na siebie pasów odcinanych i doklejanych skomplikowałoby porównywanie figur). Łatwo obliczyć, że długość odciętego pasa jest mniejsza od długości fragmentu doklejanego, czyli procedura faktycznie doprowadzi do zwiększenia pola figury.
Wypukły poliapez z odciętym i doklejonym rzędem. Podane długości rzędów odnoszą się do dłuższej podstawy trapezu. Ich pole to dwukrotność długości minus jeden.
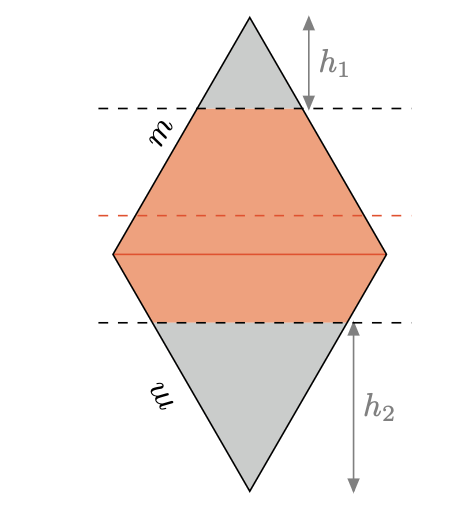
Skoro wiemy, że maksymalne poliapezy mają szerokości różniące się co najwyżej o 1, to kolejną istotną obserwacją będzie to, że osie pasów powinny przecinać się możliwie blisko siebie. Ponieważ trzy liczby różnią się co najwyżej o \(1,\) przynajmniej dwie są równe, czyli możemy myśleć o naszym poliapezie jako o wycinku rombu (części wspólnej dwóch pasów o szerokości \(m\)). Odcięliśmy od niego trójkąty o nieujemnych wysokościach \(h_1\) oraz \(h_2.\) Ponadto suma \(h_1+h_2\) jest stała. Figura składa się wówczas z \(2m^2-(h_1^2+h_2^2)\) pól. Łatwo sprawdzić, że w takiej sytuacji suma kwadratów jest tym mniejsza, im mniejsza jest różnica \(|h_1-h_2|,\) która jest dwukrotnością odległości osi trzeciego pasa od środka rombu. Jest to oczywiste, biorąc pod uwagę fakt, że w rombie im bliżej przekątnej, tym dłuższe rzędy. Pozwolimy sobie opuścić dowód algebraiczny tych obserwacji.
Ustalone dotąd własności maksymalnych poliapezów przy danym obwodzie pozwalają już dla każdego \(l\in\mathbb{N}\) wyznaczyć je jednoznacznie z dokładnością do izometrii. Okazuje się, że przedstawienie liczby naturalnej jako sumy trzech liczb różniących się o co najwyżej jeden jest jednoznaczne (kolejność nas nie interesuje), a kształt maksymalnego poliapezu o takich szerokościach również jest jednoznaczny. W zależności od reszty z dzielenia obwodu \(l\) przez \(6\) otrzymujemy więc dokładne wartości \(P_\triangleleft(l).\) Ponieważ nie rozważamy wypukłych poliapezów o szerokości \(0,\) wygodnie będzie oznaczać obwody jako \({l=6k-5, 6k-4,\ldots, 6k-1,6k}\) (ujemne reszty) dla \(k\geq 1.\)
Na rysunkach pole każdego dużego trójkąta to \(k^2,\) zaś zakolorowane trójkąty oznaczają obszary nakryte dwoma równoległobokami o polu \(2k.\)
\(2k, 2k, 2k\)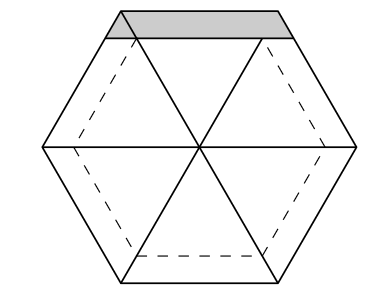
\(2k, 2k, 2k{-}1\)
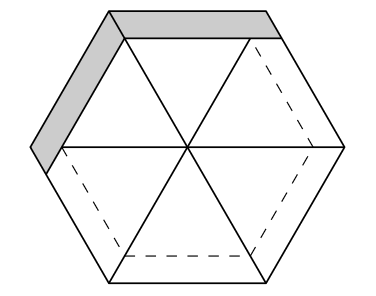\(2k, 2k{-}1, 2k{-}1\)
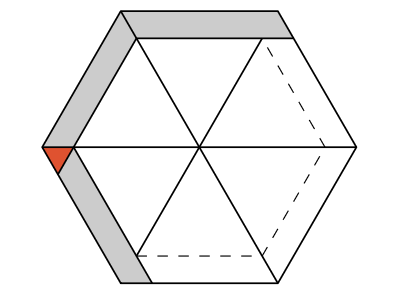\(2k{-}1, 2k{-}1, 2k{-}1\)
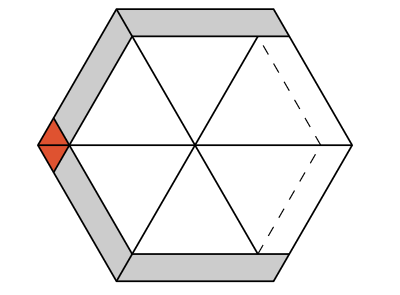\(2k{-}1, 2k{-}1, 2k{-}2\)
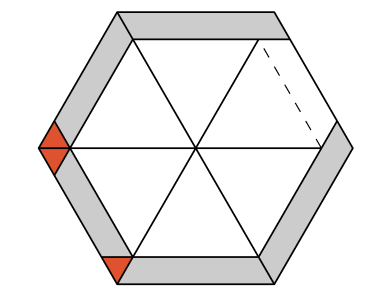\(2k{-}1, 2k{-}2, 2k{-}2\)Zauważmy, że po pomnożeniu pola przez \(6\) możemy je łatwo porównać z kwadratem liczby \(l\): \[\def\arraystretch{1.3}\begin{array}{rcll} 6P_\triangleleft(6k) = & 6^2 k^2 & = (6k)^2 & > (6k-1)^2 \\ 6P_\triangleleft(6k-1)= & 6^2 k^2-12k-6 & =(6k-1)^2 -7 & = (6k-2)^2 + 12k-10 \\ 6P_\triangleleft(6k-2)= & 6^2 k^2-2\cdot12k & =(6k-2)^2 -4 & = (6k-3)^2 + 12k-9 \\ 6P_\triangleleft(6k-3)= & 6^2 k^2-3\cdot12k+6 & =(6k-3)^2 -3 & = (6k-4)^2 + 12k-10 \\ 6P_\triangleleft(6k-4)= & 6^2 k^2-4\cdot12k+12 & =(6k-4)^2 -4 & = (6k-5)^2 + 12k-13 \\ 6P_\triangleleft(6k-5)= & 6^2 k^2-5\cdot12k+18 & =(6k-5)^2 -7 & = (6k-6)^2 + 12k-18 \end{array}\] Zatem w każdym przypadku \((l-1)^2 < 6P_\triangleleft(l) \leq l^2\) (pamiętajmy, że \(l\geq 3\); nie istnieje poliapez o obwodzie \(2\)). Po spierwiastkowaniu otrzymujemy nierówności równoważne stwierdzeniu: \(l=\left\lceil\sqrt{6P_\triangleleft(l)}\right\rceil.\)
Jeśli dobierzemy takie \(l,\) że zachodzą nierówności \(P_\triangleleft(l-1)< n \leq P_\triangleleft(l),\) otrzymamy \(l-1\leq \left\lceil\sqrt{6n}\right\rceil\leq l.\) Gdyby \(O_\triangleleft(n)< l\), wówczas \(n\leq P_\triangleleft(O_\triangleleft(n)) \leq P_\triangleleft(l-1),\) gdzie pierwsza nierówność wynika wprost z definicji \(P_\triangleleft\) i \(O_\triangleleft,\) a druga z monotoniczności \(P_\triangleleft.\) Przeczy to założeniu \(P_\triangleleft(l-1)<n\). Zatem zawsze zachodzi \(O_\triangleleft(n)\geq l\geq\left\lceil\sqrt{6n}\right\rceil.\) Zauważmy poza tym, że obwód musi być tej samej parzystości co \(n,\) ponieważ wynosi \(3n-2s,\) gdzie \(s\) to liczba wspólnych boków pól tworzących figurę. Stąd wniosek, że \[O_\triangleleft(n)\geq \min\bigl\{\ell\in\mathbb{N} : \ell\geq \sqrt{6n} \text{ i } 2| ( n-\ell) \bigr\}.\] Okazuje się, że tak naprawdę zachodzi tu równość. Najpierw rozważmy przypadek \(l=\left\lceil\sqrt{6n}\right\rceil.\) Gdy przyjrzymy się poprzednim rysunkom, zauważymy, że kolejne maksymalne poliapezy różnią się jednym rzędem pól. Zabierając kolejne komórki ze skrajnego rzędu maksymalnego poliapezu o obwodzie \(l,\) albo zwiększamy obwód o 1 (jeśli zabrane komórki tworzą trapez, ew. zdegenerowany do jednego trójkąta), albo go nie zmieniamy (gdy zabrane komórki tworzą równoległobok). Zatem faktycznie, minimalny obwód będzie alternował jednocześnie z parzystością \(n\) (stały być nie może) pomiędzy wartościami \(l\) a \(l+1.\) Niestety może się zdarzyć, że \(l=\left\lceil\sqrt{6n}\right\rceil+1.\) Zauważmy, że \(P_\triangleleft(l-1)+1\leq n,\) zatem w takim przypadku \(6P_\triangleleft(l-1)+6\leq 6n\leq (l-1)^2.\) Z trzeciej kolumny wzorów odczytujemy, że może się tak zdarzyć tylko, gdy \(l\) przystaje modulo \(6\) do \(1\) lub \(5,\) a ponadto musi być \(n=P_\triangleleft(l-1)+1=P_\triangleleft(\left\lceil\sqrt{6n}\right\rceil)+1.\) Uzyskanie pola \(n\) (oraz właściwej parzystości obwodu!) z maksymalnego poliapezu o obwodzie \(l-1=\left\lceil\sqrt{6n}\right\rceil\) jest zatem możliwe poprzez dodanie jednego trójkąta.
Korzystamy z monotoniczności funkcji \(x\mapsto\left\lceil\sqrt{6x}\right\rceil\)
Wykazaną właśnie równość można opisać zwartym wzorem: \[O_\triangleleft(n) = 2\left\lceil\frac{ n+\sqrt{6n}}{2}\right\rceil-n.\] Pokażemy bowiem, że dla liczby całkowitej \(k\) i rzeczywistej \(x\) wartość \({w(k,x)=2\left\lceil\frac{k+x}{2}\right\rceil-k}\) to najmniejsza liczba całkowita nie mniejsza od \(x\) o tej samej parzystości co \(k.\) Wprost z definicji, parzystość \(w(k,x)\) jest równa parzystości \(k,\) ponieważ sufit jest zawsze liczbą całkowitą. Z kolei wiedząc, że \(\left\lceil y\right\rceil\geq y,\) otrzymujemy \[w(k,x)\geq k+x-k=x.\] Druga nierówność, \(\left\lceil y\right\rceil< y+1,\) dowodzi, że \[w(k,x) < 2\frac{k+x+2}{2}-k=x+2.\] W otrzymanym przedziale leży dokładnie jedna liczba całkowita o tej samej parzystości co \(k.\) Zatem dowiedliśmy, że \(w(n,\sqrt{6n})\) jest równe najmniejszej liczbie całkowitej, większej od \(\sqrt{6n},\) która jest tej samej parzystości co \(n.\)
Po szczegółowym omówieniu siatki kwadratowej i trójkątnej pozostaje wyznaczyć wzór na minimalny obwód dla układów kafelków sześciokątnych. To zadanie zostawimy już jednak jako ćwiczenie Czytelnikowi.