Pola i punkty kratowe

Afiliacja: Instytut Matematyki Stosowanej i Mechaniki UW

W artykule Obliczenia pól i objętości – trzy metody geometryczne, \(\Delta^2_{25}\), opisaliśmy trzy geometryczne sposoby obliczania pól figur płaskich. Celem tego artykułu jest pokazanie, jak można aproksymować pole koła o promieniu \(r=\sqrt{n},\) gdzie \(n\) jest liczbą naturalną, za pomocą zliczania punktów kratowych zawartych w tym kole i na jego brzegu. Pokażemy także, że w przypadku wielokątów o wierzchołkach w punktach kratowych znajomość liczby punktów kratowych w ich wnętrzach i na ich brzegach wystarcza do dokładnego obliczenia pól tych wielokątów.

Carl Friedrich Gauss (1777–1855)

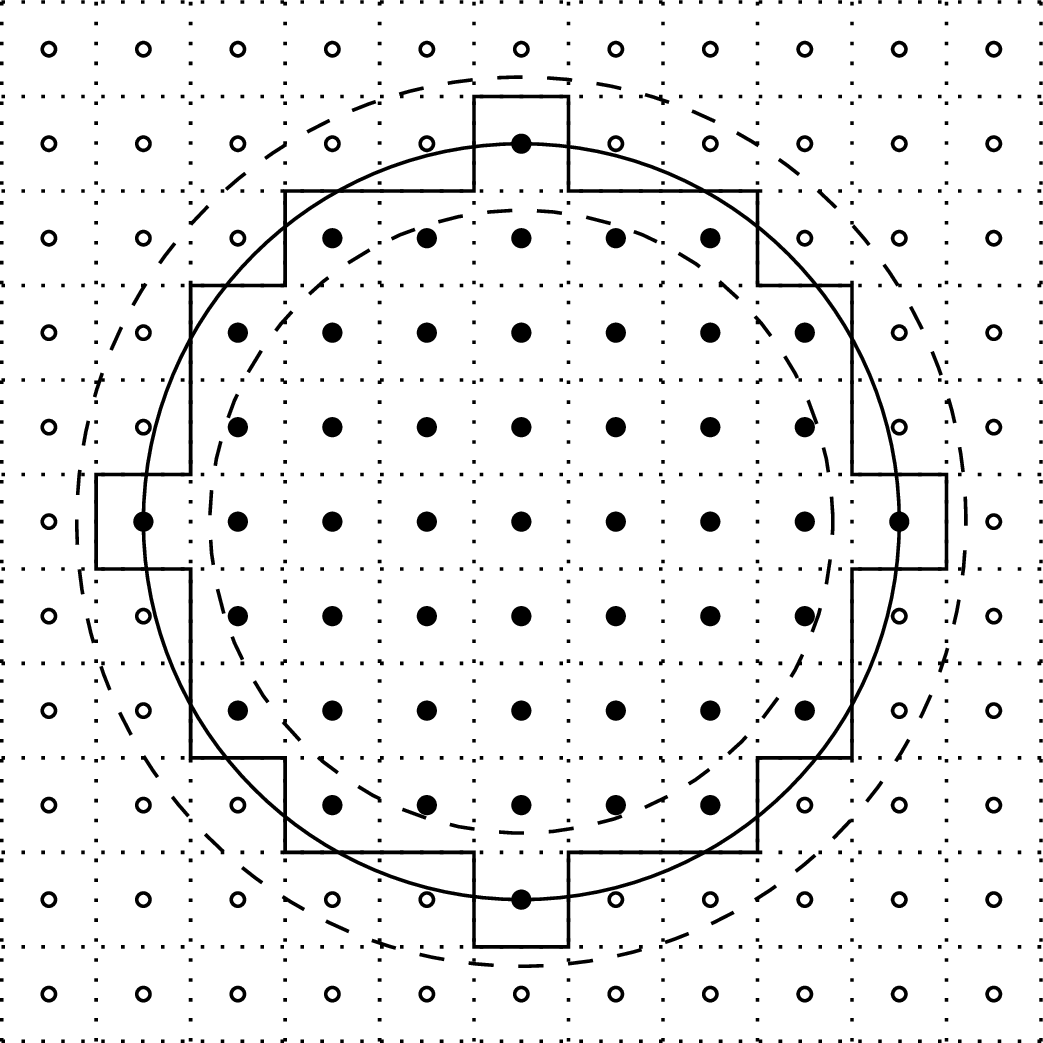
Rys. 1. Okrąg \(C(4)\) i  okręgi \(C(4 \pm \frac{\sqrt{2}}{2})\) pomagające oszacować liczbę punktów kratowych

\(r=\sqrt{n}\)	\(N(n)\)	\(N(n)/n\)
1	5	5
2	13	3,25
3	29	3,22
4	49	3,06
5	81	3,24
6	113	3,14
7	149	3,04
8	197	3,08
9	253	3,12
10	317	3,17
20	1257	3,14
30	2821	3,13
100	31417	3,1417
200	125629	3,1407
300	282697	3,1411

Rys. 2

\(r=\sqrt{n}\)	\(N(n)\)	\(N(n)/n \approx \pi\)
400	502 625	3,14141
500	785 349	3,14139
1 000	3 141 549	3,141549
10 000	314 159 221	3,141592
100 000	31 415 939 281	3,141594
200 000	125 663 759 077	3,141594

Rys. 4

Obliczenia dla okręgu.

Oznaczmy przez \(N(n)\) liczbę punktów kratowych na i wewnątrz okręgu \(C(\sqrt{n})\) o środku w początku układu współrzędnych i promieniu \(r=\sqrt{n}\) (patrz rys. 1).

Jednym z pierwszych uczonych, którzy postawili pytanie o wartość \(N(n),\) był Carl Friedrich Gauss. W roku 1837 napisał na ten temat artykuł. Podał w nim swoje obliczenia dla naturalnych \(r\) w zakresie od \(1\) do \(300,\) patrz tabela na rysunku 2. Z tabeli możemy wywnioskować, że wartości \(\frac{N(n)}{n}\) dążą do liczby \(\pi,\) gdy \(n\) rośnie nieograniczenie. Aby to pokazać, oszacujemy najpierw różnicę \(|N(n)-\pi n|.\) Skoro \(N(n)\) jest równe sumie pól kwadratów, których środki leżą na i wewnątrz okręgu \(C(\sqrt{n}),\) to jest jasne (patrz rys. 1), że \[\pi \left( \sqrt{n}-\frac{\sqrt{2}}{2} \right)^2 \leq N(n) \leq \pi \left( \sqrt{n}+\frac{\sqrt{2}}{2} \right)^2,\] skąd wynika, że \[\tag{1}\label{appro1} \left| \frac{N(n)}{n}-\pi \right| \leq \pi \left( \sqrt{\frac{2}{n}}+\frac{1}{2n} \right).\] Prawa strona ostatniej nierówności dąży do zera wraz z nieograniczonym wzrostem \(n.\) Powyższą nierówność możemy odczytać jako \[\left| \frac{N(n)-\pi n}{\pi n} \right| \leq \sqrt{\frac{2}{n}}+\frac{1}{2n},\] co oznacza, że wartość względna (w stosunku do pola koła o promieniu \(\sqrt{n}\)) różnicy pomiędzy liczbą punktów kratowych w tym kole, razem z jego brzegiem, a polem tego koła dąży do zera wraz ze wzrostem promienia tego koła. Wartość względna tej różnicy jest rzędu \(\frac{1}{\sqrt{n}},\) czyli odwrotności promienia koła.

Na podstawie tabeli z rysunku 2 można obliczyć tę różnicę z dużą dokładnością, biorąc np. za liczbę \(\pi\) jej przybliżenie Archimedesowe \(\frac{22}{7}.\)

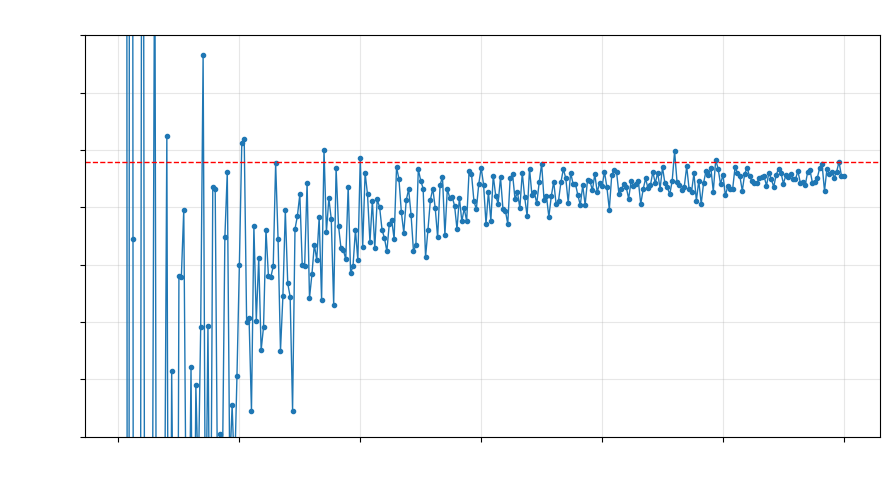Rys. 3. Ilustracja zbieżności \(N(n^2)/n^2 \to \pi\)

Wykres na rysunku 3 pokazuje, w jaki sposób \(\frac{N(r^2)}{r^2}\) zbliża się do liczby \(\pi\) wraz ze wzrostem \(r\) w zakresie \(0<r\leq 300.\) Tabela na rysunku 4 pokazuje wyliczenia dla większych wartości \(r.\)

Nasuwają się dwa pytania.

1. Czy istnieją wzory określające \(N(n)\) w zależności od \(n\)?

2. Czy może istnieją figury płaskie, dla których liczba punktów kratowych leżących w ich wnętrzu i na ich brzegu wyraża nie tylko w przybliżeniu, ale – poprzez konkretną formułę – dokładnie pola tych figur?

Na oba te pytania odpowiedź jest pozytywna. Odpowiedzią na pytanie (i) jest formuła Gaussa: \[\tag{2}\label{points} N(n)= 1 + 4 \left( \lfloor n \rfloor - \left\lfloor \frac{n}{3} \right\rfloor + \left\lfloor \frac{n}{5} \right\rfloor - \left\lfloor \frac{n}{7} \right\rfloor + \left\lfloor \frac{n}{9} \right\rfloor - \left\lfloor \frac{n}{11} \right\rfloor + \ldots \right),\] gdzie \(\lfloor\cdot\rfloor\) jest funkcją podłogi. Łatwo stąd wyznaczyć bezpośrednio wartości dla \(n=0,1,2,3,4\) (na marginesie). Z równości \(N(2)=N(3)\) możemy wywnioskować, że na okręgu \(C(\sqrt{3})\) nie ma żadnych punktów kratowych, a z tego, że \({N(4)-N(3)=4},\) wynika, że na okręgu \(C(\sqrt{4})\) jest ich \(4.\)

Podłoga \(\lfloor x \rfloor\) liczby \(x\) to największa liczba całkowita nie większa od \(x.\)
Przykładowe wartości \(N(n)\): \[\begin{aligned} N(0) & =1 \\ N(1) & =1+4=5 \\ N(2) & =1+4\cdot 2=9 \\ N(3) & =1+4\cdot 3-4=9 \\ N(4) & =1+4\cdot 4-4=13 \end{aligned}\]

Zanim przejdziemy do dowodu wzoru Gaussa, wykażemy jedną z jego konsekwencji, słynny wzór Leibniza: \[\tag{3}\label{Leibniz} \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7 } +\frac{1}{9} - \frac{1}{11} + \ldots\]

Załóżmy, że \(\sqrt{n}\) jest liczbą naturalną nieparzystą. Napiszmy wzór Gaussa \(\eqref{points}\) w postaci: \[\frac{1}{4}(N(n)-1) = \lfloor n\rfloor - \left\lfloor \frac{n}{3} \right\rfloor + \left\lfloor \frac{n}{5} \right\rfloor - \left\lfloor \frac{n}{7} \right\rfloor + \ldots \pm \left\lfloor \frac{n}{\sqrt{n}} \right\rfloor \pm \theta \sqrt{n},\] gdzie \(\theta\) jest ułamkiem właściwym. Korzystamy tu z tego, że szereg jest naprzemienny, a moduły jego wyrazów tworzą ciąg nierosnący. Wtedy moduł reszty szeregu jest nie większy od modułu pierwszego odrzuconego wyrazu, czyli \(\lfloor \frac{n}{\sqrt{n}+2}\rfloor.\) Liczba ta jest mniejsza od liczby naturalnej \(\lfloor \frac{n}{\sqrt{n}}\rfloor =\sqrt{n},\) można ją zatem zapisać jako \(\theta \sqrt{n},\) gdzie \(\theta\) jest jak wyżej.

Następny krok to zastąpienie funkcji podłogi ułamka samym ułamkiem. Ponieważ \(\frac{k}{n} - \lfloor\frac{ k}{n}\rfloor \leq 1,\) a liczba zachowanych wyrazów szeregu jest równa \(\frac{\sqrt{n}+1}{2}< \sqrt{n},\) więc \[\frac{1}{4}(N(n)-1) = n - \frac{n}{3} + \frac{n}{5} - \frac{n}{7} + \ldots \pm \frac{n}{\sqrt{n}} \pm \theta \sqrt{n} \pm \theta'\sqrt{n},\] gdzie \(\theta'\) jest także ułamkiem właściwym. Dzieląc teraz obie strony przez \(n,\) otrzymujemy \[\frac{1}{4n}(N(n)-1) = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7 } + \ldots \pm \frac{1}{\sqrt{n}} \pm \frac{\theta}{\sqrt{n}} \pm \frac{\theta'}{\sqrt{n}}\] dla liczb \(n\) przebiegających ciąg kwadratów liczb nieparzystych.

Biorąc pod uwagę zbieżność \(\frac{N(n)}{n}\to \pi\) wynikającą z oszacowania \(\eqref{appro1}\) i zbiegając z \(n\) do nieskończoności, dostajemy wzór Leibniza \(\eqref{Leibniz}\).

Przejdźmy teraz do dowodu formuły Gaussa. Jeśli przez \(R(n)\) oznaczymy liczbę punktów kratowych na okręgu \(C(\sqrt{n}),\) to \(N(n)=R(0)+R(1)+ \ldots +R(n).\) Znając wartości \(R(k)\) dla poszczególnych \(k,\) możemy obliczyć \(N(n),\) i taka też była droga odkrycia powyższej formuły Gaussa. Rzecz sprowadza się zatem do pytania o liczbę pierwiastków całkowitych \(a,b\) równania \[a^2 + b^2 = n\] dla danej liczby naturalnej \(n.\) Mamy następujące:

Twierdzenie 1 (za [Hilbert, 1956]). Liczba przedstawień liczby całkowitej \(n\) jako sumy kwadratów dwóch liczb całkowitych jest równa czterokrotności różnicy liczby dzielników liczby \(n\) o postaci \(4k+1\) i liczby dzielników o postaci \(4k+3.\)

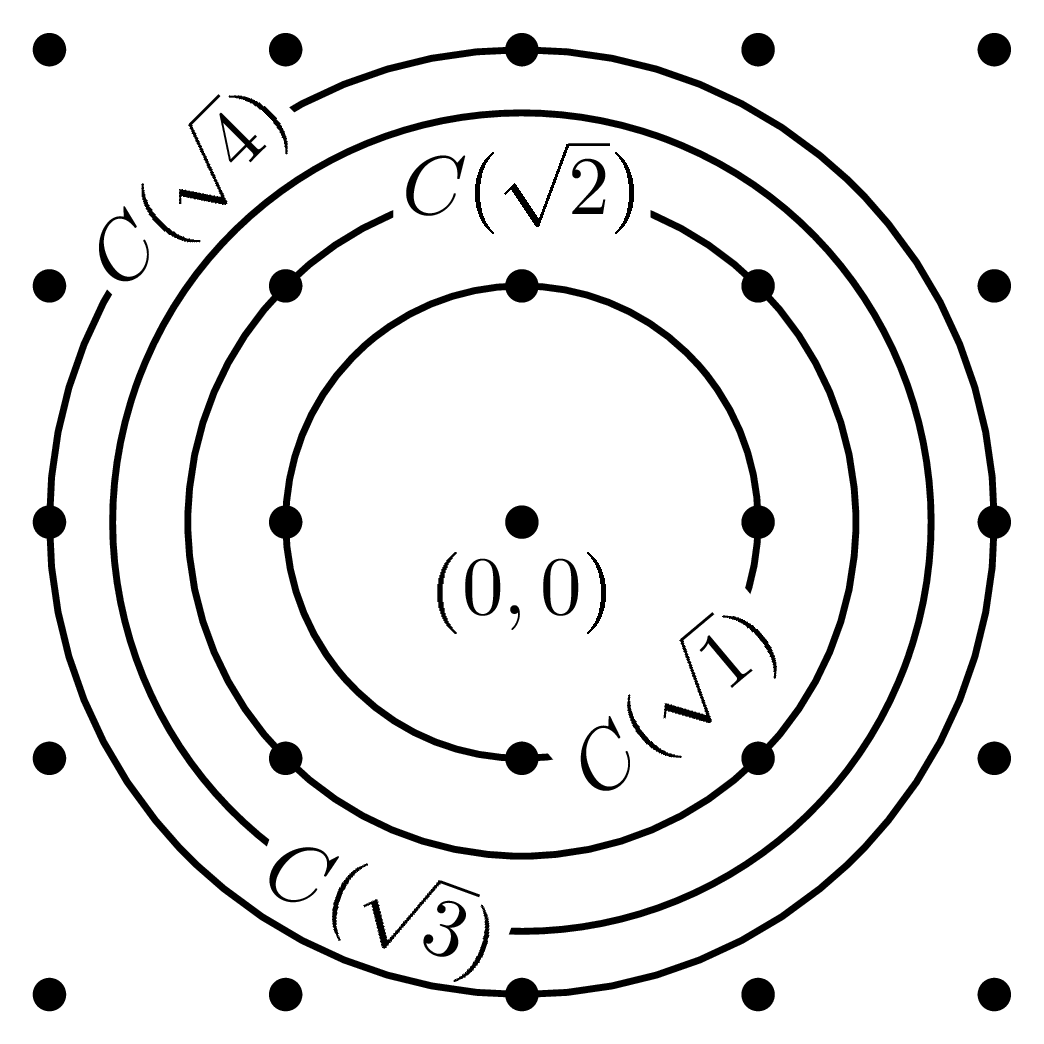
Dla przykładu \(R(3)=N(3)-N(2)=0.\) Liczba pierwsza \(3\) ma jedynie dzielniki \(1\) i \(3,\) więc na mocy powyższego twierdzenia \({R(3)=4(1-1)=0}.\) Dalej: \({R(4)=N(4)-N(3)=4}.\) Wśród dzielników liczby \(4\) (czyli \(1,2,4\)) nie ma dzielników postaci \(4k+3,\) więc z twierdzenia otrzymujemy \({R(4)=4(1-0)=4}.\) I rzeczywiście, na okręgu \(C(\sqrt{4})\) mamy cztery punkty kratowe, \((2,0),(0,2),(-2,0),(0,-2),\) będące całkowitymi rozwiązaniami równania \(a^2+b^2=4\) (patrz rys. 5).

Rys. 5. Punkty kratowe na okręgach o promieniach \(\sqrt{n}\) dla \(n=1,2,3,4\)

Bezpośrednie wykorzystanie Twierdzenia 1 dla obliczenia kolejnych \(R(n),\) a następnie równości \(N(n)=R(0)+R(1)+ \ldots +R(n)\) dla obliczenia \(N(n)\) byłoby niezmiernie żmudne dla dużych \(n.\) Jest jednak dużo prostszy sposób obliczenia \(N(n).\) Najpierw obliczamy liczbę dzielników postaci \(4k+1\) dla wszystkich liczb naturalnych \(m\) nieprzekraczających \(n\) i od tej liczby odejmujemy liczbę dzielników postaci \(4k+3,\) też dla wszystkich \(m \leq n,\) otrzymując: \[\left( \lfloor n\rfloor + \left\lfloor \frac{n}{5} \right\rfloor + \left\lfloor \frac{n}{9} \right\rfloor + \left\lfloor \frac{n}{13} \right\rfloor + \ldots \right) - \left( \left\lfloor \frac{n}{3} \right\rfloor + \left\lfloor \frac{n}{7} \right\rfloor + \left\lfloor \frac{n}{11} \right\rfloor + \ldots \right)\] Mnożąc powyższe wyrażenie przez \(4\) i dodając do niego jedynkę odpowiadającą punktowi kratowemu \((0,0),\) po przegrupowaniu wyrazów, otrzymujemy formułę \(\eqref{points}\). Bardziej formalne ujęcie rozważań przedstawionych w punkcie (i) można znaleźć w artykule Deltowym Michała Krycha [Krych, 2019].

Na przykład dla \(n=10\) wśród liczb \(1,2,\ldots,10\) mamy trzy będące postaci \(4k+1\): \(1,\) \(5,\) \(9.\) Przez \(1\) dzielą się wszystkie z powyższej dziesiątki, \(10 = \lfloor \frac{10}{1} \rfloor,\) przez \(5\) dzielą się dwie, \(2=\lfloor \frac{10}{5} \rfloor,\) przez \(9\) dzieli się tylko jedna, \(1=\lfloor \frac{10}{9} \rfloor.\) Przy tym \(\lfloor \frac{10}{13} \rfloor\) i wszystkie następne wyrazy szeregu \(\lfloor 10\rfloor + \lfloor \frac{10}{5} \rfloor + \lfloor \frac{10}{9} \rfloor + \lfloor \frac{10}{13} \rfloor + \ldots\) są równe zero.

Obliczenia dla wielokątów.

Przejdźmy do pytania (ii) o dokładne wyznaczenie pola za pomocą zliczania punktów kratowych. Jedną z możliwych odpowiedzi na to pytanie jest następujące twierdzenie z 1899 roku:

Twierdzenie Picka. Pole dowolnego prostego wielokąta \(P,\) którego wierzchołkami są punkty kratowe, jest dane wzorem \[\tag{4}\label{Pick-formula} A = W + \tfrac{1}{2} B - 1,\] gdzie \(W\) jest liczbą punktów kratowych wewnątrz \(P,\) a \(B\) jest liczbą punktów kratowych na brzegu \(P,\) wliczając wierzchołki.

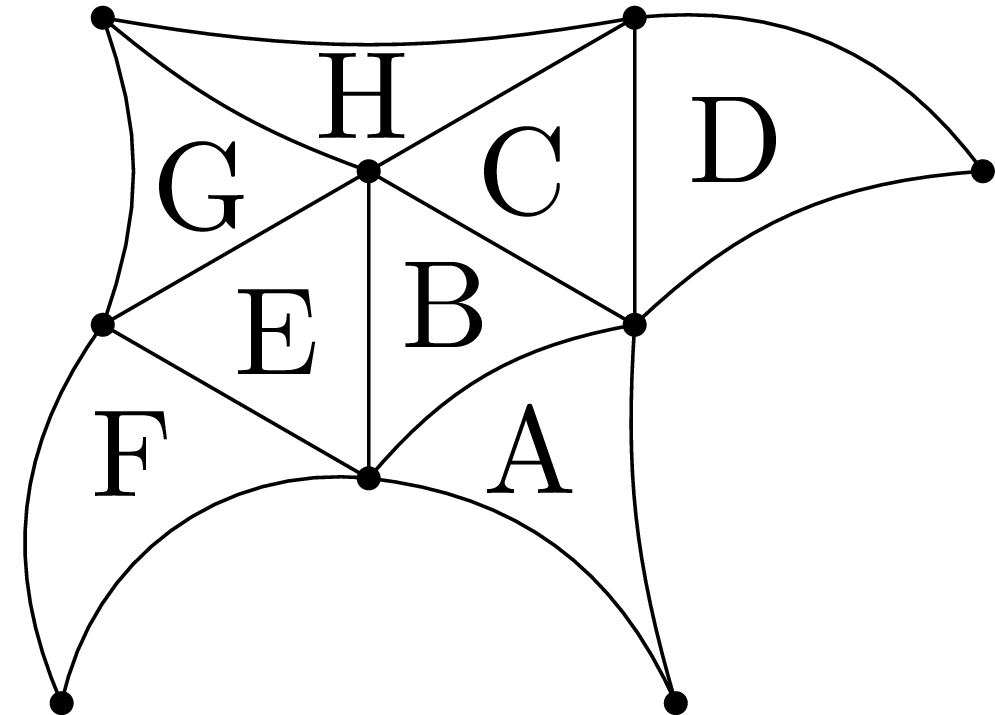
Twierdzenie Picka łączy geometryczną teorię liczb z mierzeniem pól, czyli, jak sama nazwa wskazuje, z klasyczną geometrią. Sama jego natura jest jednakże topologiczna. Aby to zobaczyć, rozważymy prostszą, ale ogólniejszą sytuację. Niech \(G\) będzie figurą płaską, złożoną z segmentów trójkątnopodobnych o tym samym polu \(d,\) tak jak to widać na rysunku 6. Oznaczmy liczbę jej wierzchołków wewnętrznych przez \(W,\) zewnętrznych przez \(B,\) liczbę krawędzi przez \(K,\) a pole figury \(G\) przez \(A.\) Przypomnijmy ponadto równość Eulera: \(V-E+F=1,\) gdzie \(V,\) \(E\) i \(F\) to, odpowiednio, liczby wierzchołków, krawędzi i ścian grafu narysowanego na płaszczyźnie bez przecinających się krawędzi.

Rys. 6. Dołączając jeden wierzchołek i dwie krawędzie do obszaru A, otrzymujemy obszar B i mamy \(3+2=3\cdot 0+2\cdot 4 -3.\) Dochodzimy w ten sposób do \(15=3\cdot 0 +2\cdot 9 -3\) dla sumy pierwszych siedmiu obszarów. Na koniec dołączamy jedną krawędź zewnętrzną, jeden wierzchołek zewnętrzny staje się wtedy wierzchołkiem wewnętrznym i mamy \(16 = 3\cdot 1 +2\cdot 8 -3\) dla całej figury

W naszej sytuacji \(V=W+B,\) \(F=\frac{A}{d}\) i \(E=K.\) Pokażemy, że \(K=3W+2B-3.\) Rzeczywiście wzór ten zachodzi dla pojedynczego obszaru trójkątnopodobnego, gdyż mamy wtedy \(K=3,\) \(W=0,\) \(B=3\) i \(3=3\cdot 0+2\cdot 3 -3.\) Jeśli do tego obszaru dołączymy podobny, przylegający do niego element naszej wyjściowej figury, to prawdziwość tego wzoru się nie zmieni, i tak będzie aż do ułożenia całej figury – rysunek 6 ilustruje, w jaki sposób dodawać kolejne obszary. Wstawiając teraz postać \(V,\) \(E\) i \(F\) do równości Eulera, dostaniemy \[A = 2dW +dB -2d.\] Dla \(d=\frac{1}{2}\) otrzymujemy stąd równanie \(\eqref{Pick-formula}\).

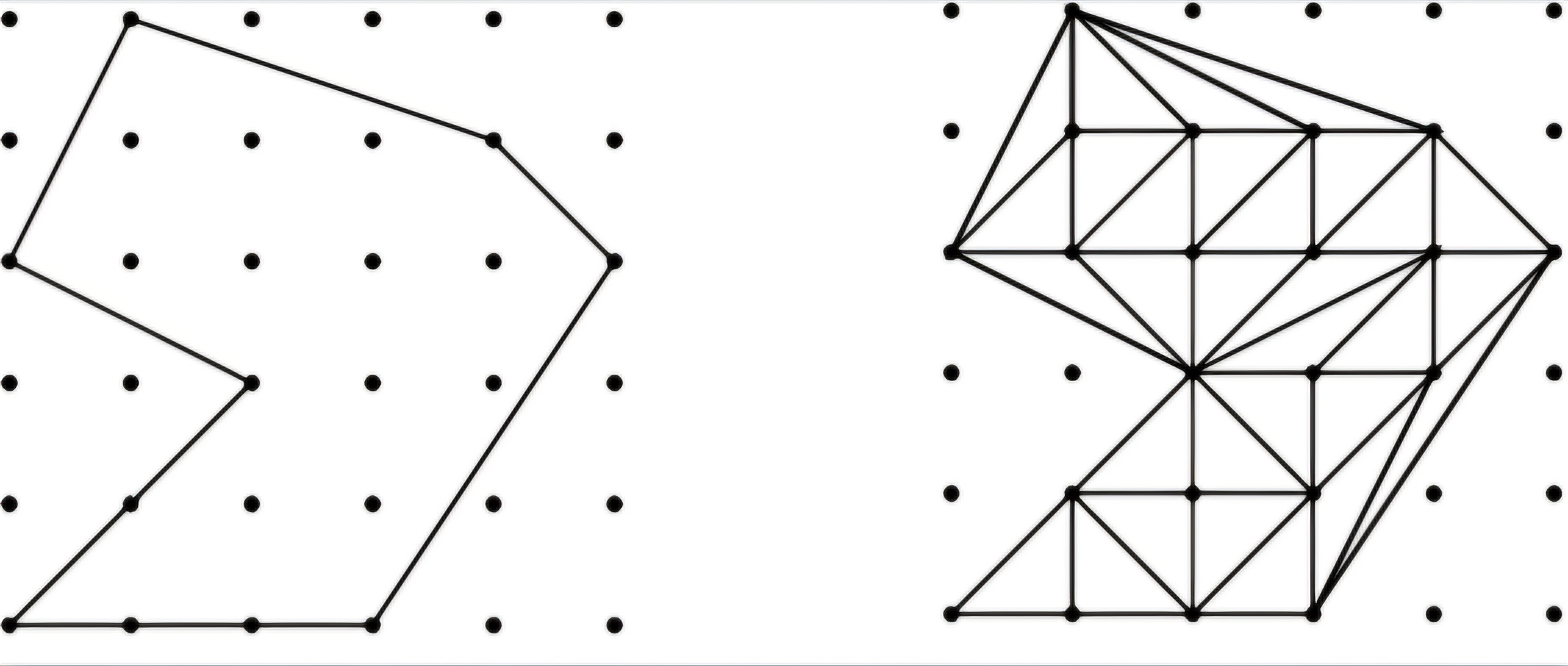
Rys. 7. Pole figury po lewej stronie obliczone ze wzoru \(\eqref{Pick-formula}\) jest równe \(A=11+\frac{1}{2}10 -1 = 15.\) Po prawej stronie jedna z triangulacji tej figury. Każdy z \(30\) trójkątów podstawowych ma pole równe \(\frac 12\)

Dla dowodu twierdzenia Picka wystarczy pokazać, po pierwsze, że każdy obszar z założeń tego twierdzenia można rozłożyć na trójkąty podstawowe, to znaczy niezawierające punktów kratowych w swoich wnętrzach ani na swoich bokach (z wyjątkiem wierzchołków) – dowód tej własności pomijamy, po drugie, że pole każdego trójkąta podstawowego jest równe \(\frac{1}{2}\) i po trzecie, że dla całego obszaru zachodzi równość \({K=3W+2B-3}.\)

To, że pole każdego trójkąta podstawowego jest równe \(\frac{1}{2},\) wynika z rozumowania użytego dla dowodu nierówności \(\eqref{appro1}\). Każdy trójkąt podstawowy można uzupełnić do równoległoboku niemającego punktów kratowych w swoim wnętrzu ani na krawędziach, a więc równoległoboku generującego siatkę opartą na punktach kratowych. Załóżmy, że pole równoległoboku siatki jest równe \(\alpha.\) Wykorzystując otrzymaną siatkę do aproksymacji pola koła, podobnie jak powyżej, otrzymujemy: \[% \bigg| \alpha\frac{N(n)}{n}-\pi \bigg| \leq \frac{4D\pi}{\sqrt{n}},\] gdzie \(D\) jest średnicą równoległoboku siatki. Jako że \(\frac{N(n)}{n} \to \pi\) wraz ze wzrostem \(n,\) to \(\alpha=1,\) a stąd \(\frac{\alpha}{2}=\frac{1}{2}.\)

Dowód równości \(K=3W+2B-3\) dla obszaru wielobocznego przeprowadzamy jak powyżej, dobudowując kolejne trójkąty podstawowe.

Warto porównać przedstawiony schemat dowodu twierdzenia Picka z dowodem Cauchy’ego równania Eulera dla wielościanów [Lakatos, 2005, str. 28–32], aby zdać sobie sprawę z czyhających pułapek natury topologicznej w trakcie dowodzenia metodą triangulacji. Na temat twierdzenia Picka, rozmaitych jego dowodów i uogólnień istnieje obszerna literatura. O powiązaniu tego twierdzenia z równaniem Eulera przeczytać można np. w [Detemple, 1974]. Ciekawe fizyczne intuicje związane z twierdzeniem Picka przedstawił Jarosław Górnicki w  artykule „Wodny” dowód twierdzenia Picka (\(\Delta^{12}_{24}\)).