Sortowanie naleśników

Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski

Jacob Eli Goodman (pod pseudonimem Harry Dweighter) w roku 1975 zamieścił w The American Mathematical Monthly następujący problem: „Nasz szef kuchni jest niechlujny, i gdy przygotowuje stos naleśników, wychodzą one wszystkie różnej wielkości. Dlatego, gdy niosę je klientowi, w drodze do stolika porządkuję je (aby najmniejszy znalazł się na górze i kolejno aż do największego na spodzie) chwytając kilka z góry i odwracając je, powtarzając tę czynność (zmieniając liczbę odwracanych [naleśników]) tyle razy, ile jest to konieczne. Jeśli jest \(n\) naleśników, jaka jest maksymalna liczba odwróceń (jako funkcja \(n\)), które będę musiał wykonać, aby je uporządkować?”

Warto przy okazji wspomnieć, że 2 lutego obchodzimy Dzień Naleśnika, zaś w tym roku 12 lutego wypada Tłusty Czwartek. Smacznego!

Funkcję, o której mowa powyżej, oznaczamy \(f(n).\) Stos naleśników reprezentujemy jako permutację liczb od 1, która reprezentuje najmniejszy naleśnik, do \(n,\) która reprezentuje największy naleśnik, gdzie \(n\ge2.\) Porządkowanie naleśników odpowiada sortowaniu rosnąco elementów permutacji przez odwracanie kolejności elementów w jej prefiksach, dlatego problem pojawia się w literaturze również pod nazwą sorting by prefix reversal. Sortowanie permutacji \((4,6,2,5,1,3)\) może wyglądać na przykład tak (liczba nad strzałką oznacza długość odwracanego prefiksu): \[\begin{aligned} (4,6,2,5,1,3) & \xrightarrow{3} (2,6,4,5,1,3) \xrightarrow{4} (5,4,6,2,1,3) \\& \xrightarrow{2} (4,5,6,2,1,3)\ \xrightarrow{5} (1,2,6,5,4,3) \\&\xrightarrow{6} (3,4,5,6,2,1) \xrightarrow{4} (6,5,4,3,2,1) \xrightarrow{6} (1,2,3,4,5,6). \end{aligned}\] Aby posortować dowolną permutację, rozważamy kolejno elementy \({t=n,n-1,\dots,3},\) zachowując niezmiennik, że elementy większe od \(t\) są już na właściwych pozycjach. Jeśli \(t\) nie jest na pozycji \(t\) ani na początku permutacji, to jest na pozycji od 2 do \(t-1\) i odwracamy tyle elementów, aby element \(t\) znalazł się na początku permutacji. Jeśli \(t\) jest już na początku permutacji, to odwracamy \(t\) elementów, co umieszcza \(t\) na pozycji \(t.\) W ten sposób za pomocą co najwyżej \(2(n-2)\) odwróceń umieszczamy na docelowych pozycjach elementy od 3 do \(n.\) Jeśli po tym elementy 1 i 2 nie są we właściwej kolejności, to za pomocą jednego odwrócenia ustawiamy je w takiej kolejności. Powyższy algorytm pokazuje, że \(f(n)\le2n-3\) dla \(n\ge2.\)

E. Győri, G. Turán, Stack of pancakes (1978).

W.H. Gates, Ch.H. Papadimitriou, Bounds for sorting by prefix reversal (1979).

Przedstawimy teraz lepszy algorytm. Wymyślili go Ervin Győri i György Turán oraz niezależnie od nich William Henry Gates III (bardziej znany jako Bill Gates) i Christos Harilaos Papadimitriou. Równolegle z opisem samego algorytmu będziemy analizować jego złożoność, a w tym celu potrzebujemy wprowadzić pewne definicje. Dwa elementy na sąsiednich pozycjach permutacji tworzą dobre sąsiedztwo, jeśli ich wartości różnią się o 1. Przyjmujemy ponadto, że dobre sąsiedztwo tworzą też elementy 1 i \(n.\) Maksymalny podciąg elementów (co najmniej dwóch) tworzących dobre sąsiedztwa nazywamy blokiem. Element nienależący do żadnego bloku nazywamy wolnym. Przykładowo w permutacji \((3,5,4,7,1,2,6)\) mamy dobre sąsiedztwa \((5,4),\) \((7,1)\) i \((1,2),\) bloki \((5,4)\) i \((7,1,2)\) oraz elementy wolne 3 i 6. Dodawanie liczby całkowitej do elementu permutacji lub odejmowanie liczby całkowitej od elementu permutacji wykonujemy cyklicznie: \(n+1=1,\) \(n+2=2,\) \(1-1=n,\) \(1-2=n-1\) itd. Przyjmujemy, że po wykonaniu \(\ell\) odwróceń potencjał uzyskanej permutacji jest równy \({\Phi_\ell=\ell+\alpha w+\beta b},\) gdzie \(w\) jest liczbą elementów wolnych w tej permutacji, \(b\) jest liczbą bloków w tej permutacji, a \(\alpha\) i \(\beta\) są pewnymi stałymi, których wartości wyznaczymy później. Przez \(\Delta\Phi\) oznaczamy zmianę potencjału w sekwencji odwróceń. Wielokropkiem zastępujemy podciąg elementów permutacji nietworzący dobrych sąsiedztw z elementami go poprzedzającym i następującym po nim. Wielokropek może też oznaczać podciąg pusty. Podkreśleniem zastępujemy podciąg bloku, być może pusty. Niech \(d\in\{-1,1\}.\) Zależnie od postaci permutacji rozpatrujemy następujące przypadki, za każdym razem przedstawiając również odwrócenia, jakich należy wówczas dokonać.

1. Permutacja zaczyna się elementem wolnym \(t.\)

   1. Istnieje element wolny \(t+d\): \[(t,\dots,t+d,\dots) \to (\dots,t,t+d,\dots).\] Jedno odwrócenie zamienia dwa elementy wolne w jeden blok, czyli \(\Delta\Phi=1-2\alpha+\beta.\)

   2. Istnieje blok zaczynający się elementem \(t+d\): \[(t,\dots,t+d,\underline{\phantom{\dots}},\dots) \to (\dots,t,t+d,\underline{\phantom{\dots}},\dots).\] Jedno odwrócenie zmniejsza o jeden liczbę elementów wolnych, czyli \(\Delta\Phi=1-\alpha.\)

   3. Istnieją bloki kończące się elementami \(t+d\) i \(t-d\): \[\begin{gathered} (t,\dots,\underline{\phantom{\dots}},t+d,\dots,\underline{\phantom{\dots}},t-d,\dots) \\ \begin{aligned} & \to (t+d,\underline{\phantom{\dots}},\dots,t,\dots,\underline{\phantom{\dots}},t-d,\dots) \\&\to (\dots,\underline{\phantom{\dots}},t+d,t,\dots,\underline{\phantom{\dots}},t-d,\dots) \\&\to (t-d,\underline{\phantom{\dots}},\dots,t,t+d,\underline{\phantom{\dots}},\dots) \\&\to (\dots,\underline{\phantom{\dots}},t-d,t,t+d,\underline{\phantom{\dots}},\dots). \end{aligned} \end{gathered}\] Cztery odwrócenia zmniejszają o jeden liczby elementów wolnych i bloków, czyli \({\Delta\Phi=4-\alpha-\beta}.\)

2. Permutacja zaczyna się blokiem o długości \(k,\) gdzie \(1<k<n-1.\) Pierwszym elementem bloku jest \(t,\) a ostatnim \(t+(k-1)d.\)

   1. Istnieje element wolny \(t-d\): \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,t-d,\dots) \\\to (\dots,t+(k-1)d,\underline{\phantom{\dots}},t,t-d,\dots). \end{gathered}\] Jedno odwrócenie zmniejsza o jeden liczbę elementów wolnych, czyli \(\Delta\Phi=1-\alpha.\)

   2. Istnieje blok zaczynający się elementem \(t-d\): \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,t-d,\underline{\phantom{\dots}},\dots) \\\to (\dots,t+(k-1)d,\underline{\phantom{\dots}},t,t-d,\underline{\phantom{\dots}},\dots). \end{gathered}\] Jedno odwrócenie zmniejsza o jeden liczbę bloków, czyli \(\Delta\Phi=1-\beta.\)

   3. Istnieją blok kończący się elementem \(t-d\) i element wolny \(t+kd.\) Zależnie od ich wzajemnego położenia stosujemy odwrócenia \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,\underline{\phantom{\dots}},t-d,\dots,t+kd,\dots) \\ \begin{aligned} & \to (t+kd,\dots,t-d,\underline{\phantom{\dots}},\dots,t+(k-1)d,\underline{\phantom{\dots}},t,\dots) \\&\to (\dots,\underline{\phantom{\dots}},t-d,\dots,t+kd,t+(k-1)d,\underline{\phantom{\dots}},t,\dots) \\&\to (t,\underline{\phantom{\dots}},t+(k-1)d,t+kd,\dots,t-d,\underline{\phantom{\dots}},\dots) \\&\to (\dots,t+kd,t+(k-1)d,\underline{\phantom{\dots}},t,t-d,\underline{\phantom{\dots}},\dots) \end{aligned} \end{gathered}\] lub \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,t+kd,\dots,\underline{\phantom{\dots}},t-d,\dots) \\ \begin{aligned} & \to (t+kd,\dots,t+(k-1)d,\underline{\phantom{\dots}},t,\dots,\underline{\phantom{\dots}},t-d,\dots) \\&\to (\dots,t+kd,t+(k-1)d,\underline{\phantom{\dots}},t,\dots,\underline{\phantom{\dots}},t-d,\dots) \\&\to (t-d,\underline{\phantom{\dots}},\dots,t,\underline{\phantom{\dots}},t+(k-1)d,t+kd,\dots) \\&\to (\dots,\underline{\phantom{\dots}},t-d,t,\underline{\phantom{\dots}},t+(k-1)d,t+kd,\dots). \end{aligned} \end{gathered}\] Cztery odwrócenia zmniejszają o jeden liczby elementów wolnych i bloków, czyli \({\Delta\Phi=4-\alpha-\beta}.\)

   4. Istnieje blok, którego pierwszym elementem jest \(t+kd\): \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,t+kd,\underline{\phantom{\dots}},\dots) \\ \begin{aligned} & \to (t+(k-1)d,\underline{\phantom{\dots}},t,\dots,t+kd,\underline{\phantom{\dots}},\dots) \\&\to (\dots,t,\underline{\phantom{\dots}},t+(k-1)d,t+kd,\underline{\phantom{\dots}},\dots). \end{aligned} \end{gathered}\] Istnieje blok, którego ostatnim elementem jest \(t+kd\): \[\begin{gathered} (t,\underline{\phantom{\dots}},t+(k-1)d,\dots,\underline{\phantom{\dots}},t+kd,\dots) \\ \begin{aligned} & \to (t+kd,\underline{\phantom{\dots}},\dots,t+(k-1)d,\underline{\phantom{\dots}},t,\dots) \\&\to (\dots,\underline{\phantom{\dots}},t+kd,t+(k-1)d,\underline{\phantom{\dots}},t,\dots). \end{aligned} \end{gathered}\] Dwa odwrócenia zmniejszają o jeden liczbę bloków, czyli \(\Delta\Phi=2-\beta.\)

3. Jeśli permutacja nie pasuje do żadnego z powyższych przypadków, to jest blokiem. Jeśli nie jest to permutacja \((1,\underline{\phantom{\dots}},n),\) to zależnie od jej postaci mamy następujące przypadki:

   1. \((n,\underline{\phantom{\dots}},1) \xrightarrow{n} (1,\underline{\phantom{\dots}},n),\)

   2. \((n-1,\underline{\phantom{\dots}},1,n) \xrightarrow{n-1} (1,\underline{\phantom{\dots}},n)\) dla \(n\ge3,\)

   3. \((n,1,\underline{\phantom{\dots}},n-1) \xrightarrow{n} (n-1,\underline{\phantom{\dots}},1,n) \xrightarrow{n-1}\) \((1,\underline{\phantom{\dots}},n)\) dla \(n\ge3,\)

   4. \((2,\underline{\phantom{\dots}},n,1) \xrightarrow{n-1} (n,\underline{\phantom{\dots}},1) \xrightarrow{n} (1,\underline{\phantom{\dots}},n)\) dla \(n\ge3,\)

   5. \((1,n,\underline{\phantom{\dots}},2) \xrightarrow{n} (2,\underline{\phantom{\dots}},n,1)\) dla \(n\ge3\) i dalej jak w punkcie 3.d,

   6. \((t+1,\underline{\phantom{\dots}},n,1,\underline{\phantom{\dots}},t) \xrightarrow{n-t}\) \((n,\underline{\phantom{\dots}},t+1,1,\underline{\phantom{\dots}},t) \xrightarrow{n} (t,\underline{\phantom{\dots}},1,t+1,\underline{\phantom{\dots}},n) \xrightarrow{t}\) \((1,\underline{\phantom{\dots}},n)\) dla \(2 \le t\le n-2,\)

   7. \((t,\underline{\phantom{\dots}},1,n,\underline{\phantom{\dots}},t+1) \xrightarrow{n} (t+1,\underline{\phantom{\dots}},n,1,\underline{\phantom{\dots}},t)\) dla \(2 \le t\le n-2\) i dalej jak w punkcie 3.f.

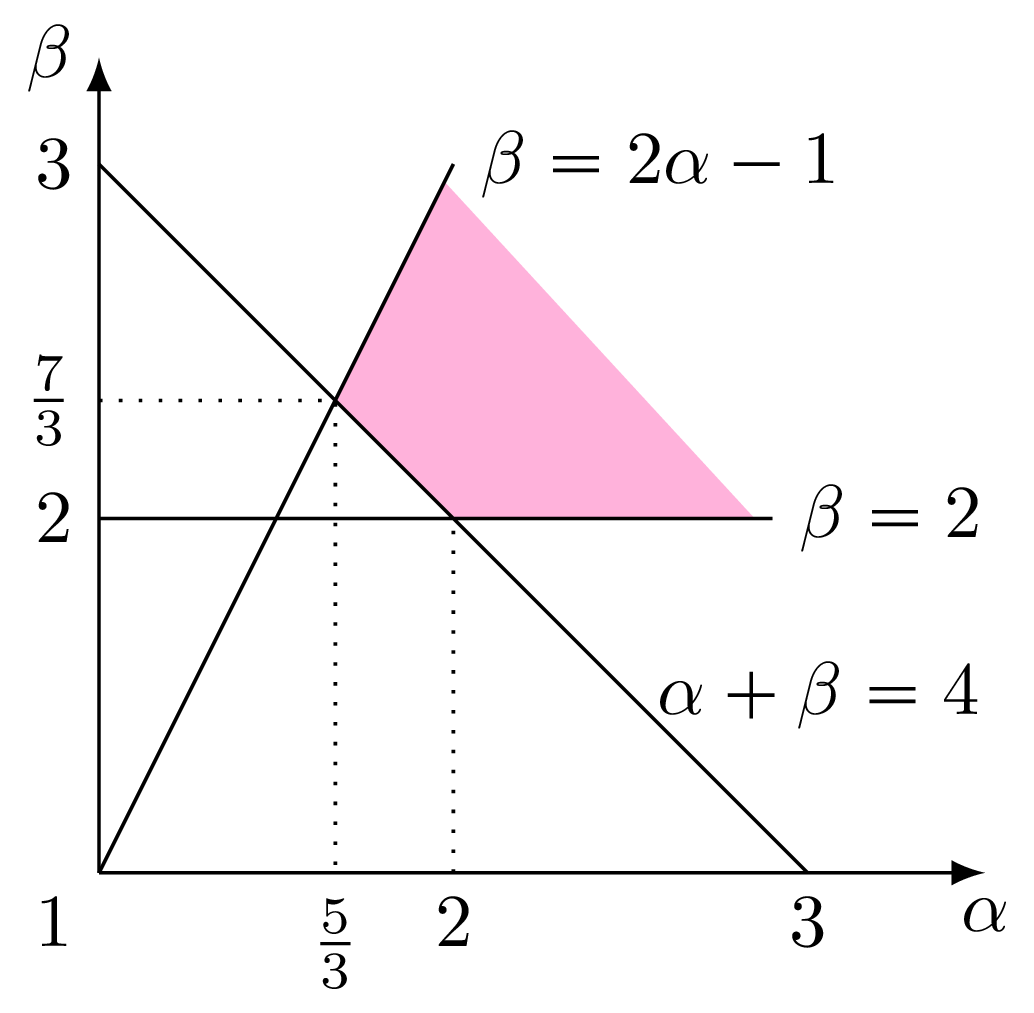
Będziemy wymagać, aby po odwróceniach z punktów 1 i 2 potencjał permutacji nie zwiększał się, czyli \(\Delta\Phi\le0,\) więc muszą być spełnione nierówności: \[\tag{1}\label{alphabeta} \begin{gathered} \alpha\ge1,\\ \alpha+\beta\ge4,\\ 2\le\beta\le2\alpha-1. \end{gathered}\]

Potencjał \(\Phi_0\) początkowej permutacji wynosi \(\alpha w+\beta b.\) Ponieważ każdy blok zawiera co najmniej dwa elementy, więc \(w\le n-2b,\) czyli \(\Phi_0\le\alpha n+(\beta-2\alpha)b.\) Korzystając z ostatniej nierówności w (1), dostajemy \(\Phi_0\le\alpha n-b\le\alpha n.\) Równość \(\Phi_0=\alpha n\) zachodzi, gdy permutacja ma \(n\) elementów wolnych. Każda sekwencja odwróceń z punktów 1 i 2 zmniejsza liczbę elementów wolnych lub bloków, więc po skończonej liczbie \(m\) odwróceń dochodzimy do punktu 3. Wtedy \(\Phi_m=m+\beta.\) W punkcie 3, aby dokończyć sortowanie, wykonujemy co najwyżej cztery odwrócenia, zatem \(f(n)\le m+4=\Phi_m-\beta+4.\) Ponieważ założyliśmy, że potencjał permutacji nie rośnie, więc \(\Phi_m\le\Phi_0\) i stąd \(f(n)\le\alpha n-\beta+4.\) Pozostaje znaleźć rozwiązanie układu nierówności (1) minimalizujące wartość \(\alpha.\) Jest to przykład zagadnienia programowania liniowego. Dla dwóch niewiadomych możemy je rozwiązać, stosując interpretację geometryczną, patrz rysunek na marginesie. Otrzymujemy \(\alpha=\frac{5}{3}\) i \(\beta=\frac{7}{3}.\) Zatem \(f(n)\le5(n+1)/3.\)

Nieco lepsze górne oszacowanie \(f(n)\le(18/11)n+O(1)\) udowodnił Bhadrachalam Chitturi ze współpracownikami. Ich dowód wymaga jednak rozpatrzenia 2220 przypadków. Znamy dokładnie wartości \(f(n)\) dla \(n\le19,\) patrz tabela niżej (jest to ciąg o numerze A058986 w The On-Line Encyclopedia of Integer Sequences).

B. Chitturi et al., An \((18/11)n\) upper bound for sorting by prefix reversals (2009).

W mojej pracy Note on pancake sorting, opublikowanej w czasopiśmie Information Processing Letters, zajmowałem się oszacowaniami dolnymi. Skonstruowałem dla większych \(n\) permutacje świadczące, że \({f(n)\ge\lfloor (15n+9)/14 \rfloor}.\)

Na koniec zauważmy, że w całym artykule milcząco zakładaliśmy, że strony naleśnika są nierozróżnialne. Każdy, kto smażył naleśniki, wie jednak, że zwykle jedna strona wychodzi bardziej przysmażona. Rozważa się więc wersję problemu sortowania naleśników tak, aby wszystkie były zwrócone przysmażoną stroną w dół, ale o tym innym razem.