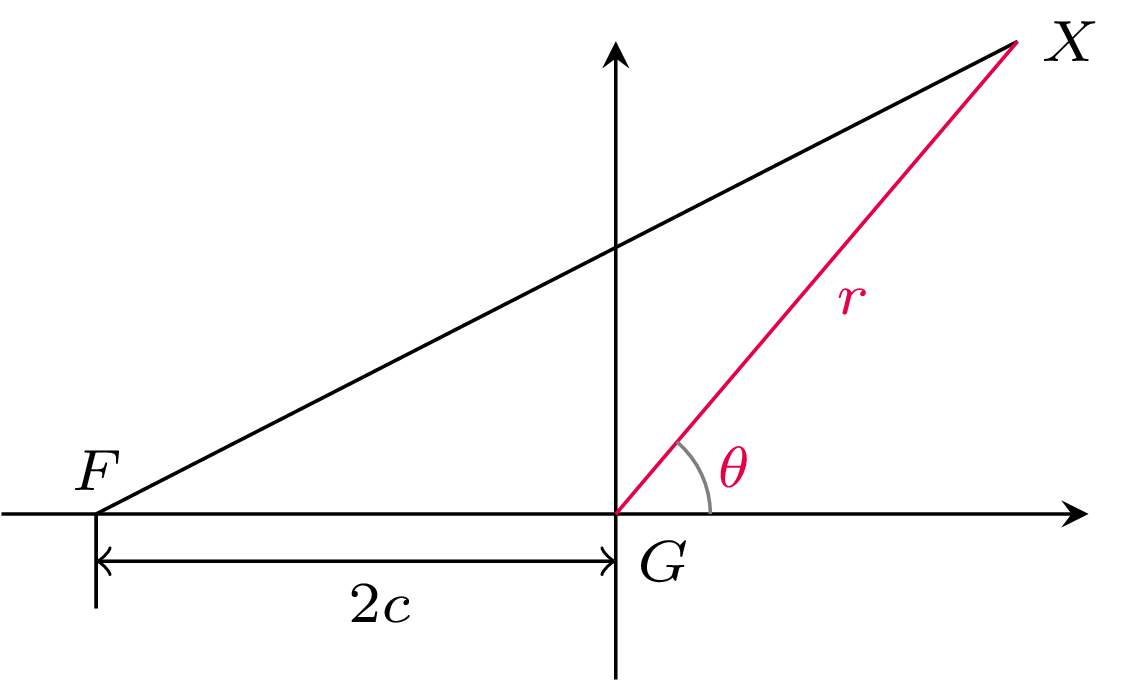Prawo powszechnego ciążenia

Jedna z najbardziej zdumiewających cech matematyki to fakt, że obiekty czy też zjawiska z pozoru niczym ze sobą niepowiązane okazują się ni stąd ni zowąd bliskimi krewnymi. Wiadomo na przykład, że jedyne trajektorie ciał niebieskich w polu grawitacyjnym Słońca to dokładnie te krzywe, które otrzymuje się z przecięcia stożka płaszczyzną, to znaczy okrąg, elipsa, parabola lub hiperbola.

Jak jednak spostrzec związek między cięciem stożka płaszczyzną a ruchem ciał niebieskich?! Pełna odpowiedź na to pytanie to jeden z największych triumfów w historii matematyki. Jego autorem jest oczywiście Izaak Newton (choć preludium napisał Johannes Kepler).

W kultowych ,,Wykładach z historii matematyki” Marka Kordosa (a także w ${\mathrm{\Delta }}_{81}^8$, w artykule Piotra Mankiewicza) znaleźć można rekonstrukcję rozumowania Newtona oraz słynny dialog pomiędzy Newtonem a odwiedzającym go Halleyem:

,,Halley: Jak wyglądałaby siła, która powoduje, że planety krążą po orbitach eliptycznych?
Newton: Odwrotność kwadratu.
Halley: Skąd pan to wie?
Newton: Po prostu obliczyłem”.

W tym artykule nie będziemy odtwarzać rozumowania angielskiego geniusza. Pokażemy tylko, jak w możliwie najprostszy sposób wydedukować z eliptycznego ruchu planet (Kepler) siłę, która na te planety działa (Newton).

Elipsa na trzy sposoby

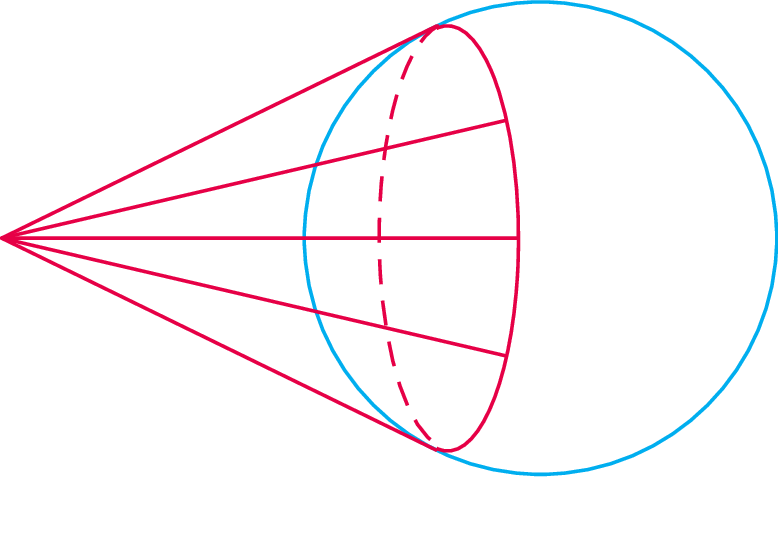
Żeby zorientować się, jakie równanie ma owalna krzywa powstająca z odpowiedniego przecięcia stożka płaszczyzną, wyobraźmy sobie dwie sfery, z których każda jest jednocześnie styczna do stożka i do płaszczyzny tnącej. W przekroju zawierającym oś symetrii stożka wyglądać to będzie jak na rysunku 1.

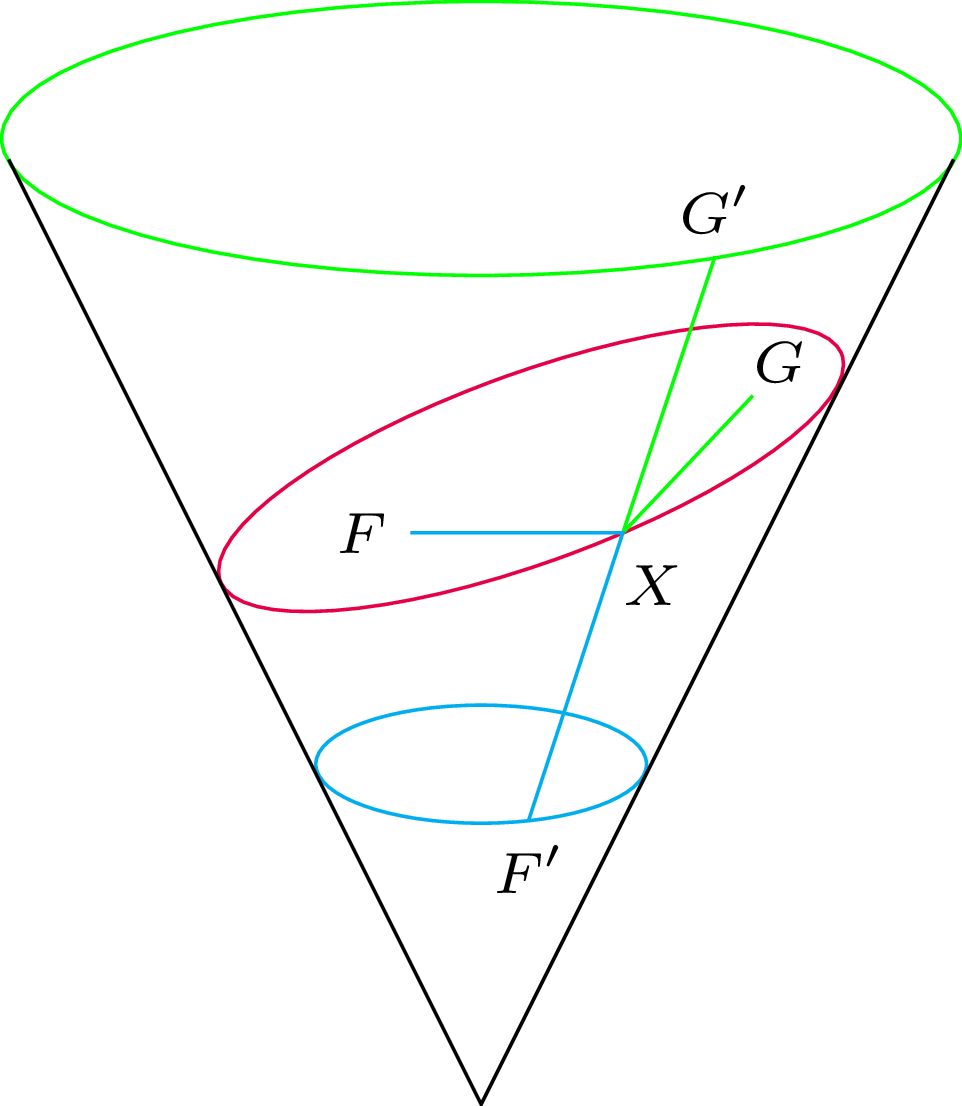
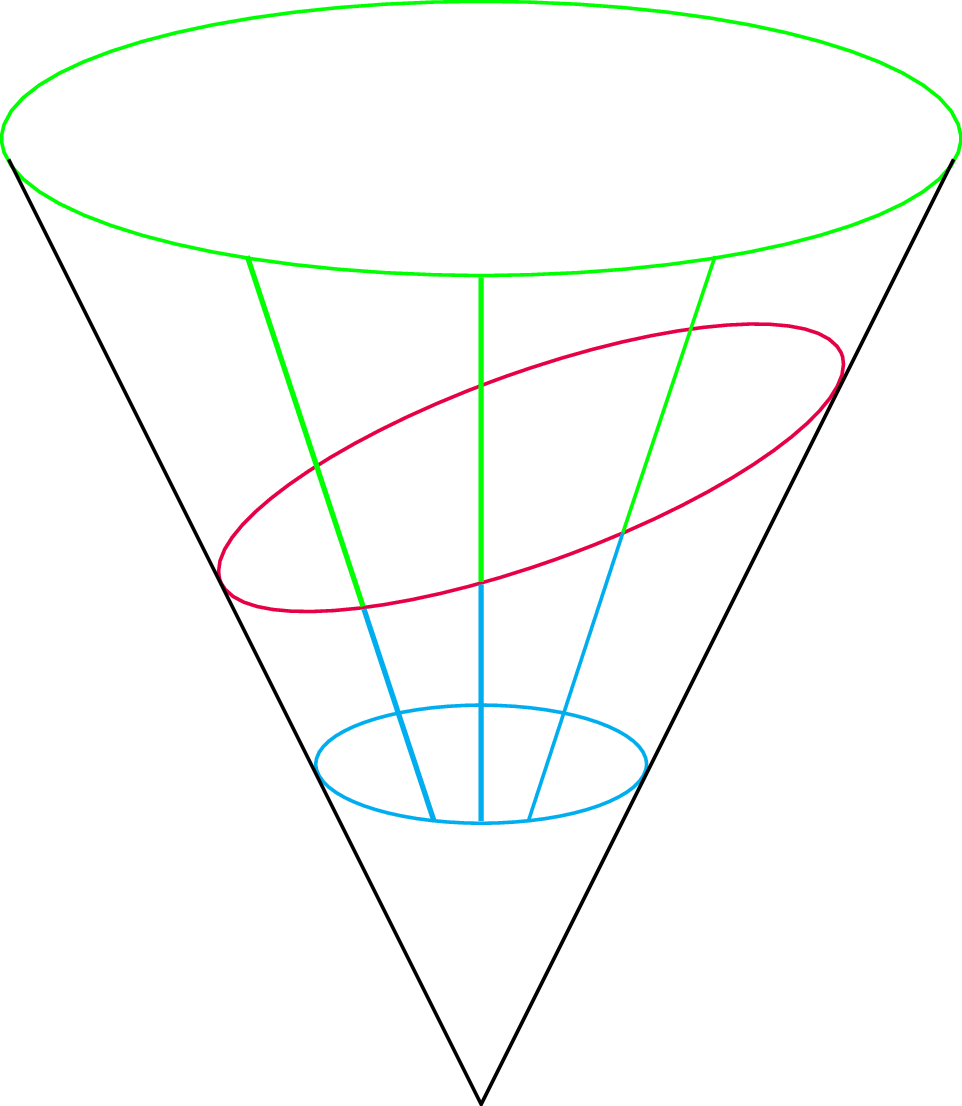
Oznaczmy przez $F$ i $G$ punkty styczności sfer z płaszczyzną (punkty te nazywać będziemy ogniskami elipsy). Zauważmy też, że punkty styczności sfer ze stożkiem tworzą dwa okręgi na powierzchni stożka. Niech odległość między tymi okręgami będzie równa $2a$. Niech też $F^{\prime }{G}^{\prime }$ będzie jakimkolwiek odcinkiem długości $2a$ łączącym oba okręgi styczności. Oznaczmy przez $X$ punkt na odcinku $F^{\prime }{G}^{\prime }$, który należy do elipsy. Korzystając z tego, że dwa odcinki o tym samym początku styczne do tej samej sfery muszą być równej długości (rys. 2), mamy $|FX|=|F^{\prime }X|$ oraz $|G^{\prime }X|=|GX|$ (rys. 3), czyli $$|FX|+|GX|=|F^{\prime }X|+|G^{\prime }X|=2a.$$ A zatem krzywa, którą otrzymaliśmy z przecięcia stożka, jest złożona z punktów, których suma odległości od punktów $F$ i $G$ jest stale równa $2a$ (rys. 4). Jest to jedna z możliwych definicji elipsy (punkty $F$ i $G$ nazywamy wówczas jej ogniskami).

Znajdźmy teraz równanie elipsy w biegunowym układzie współrzędnych o środku w ognisku $G$. Niech $X$ będzie punktem na elipsie w odległości $r$ od $G$ i niech kąt pomiędzy $GX$ a osią iksów będzie równy $\theta$ (rys. 5). Z wyprowadzonej własności elipsy wynika, że $|FX|=2a-r$.

Oznaczając teraz odległość ognisk $F$ i $G$ przez $2c$ i korzystając z twierdzenia cosinusów w trójkącie $FGX$, mamy $$(2a-r{)}^2=(2c{)}^2+r^2-4cr\cos ({180}^{\circ }-\theta ).$$ Po standardowych przekształceniach dostajemy: $$r=\frac{\alpha }{1+\epsilon \cos \theta },$$ gdzie $\alpha =\frac{a^2-c^2}{a}$, $\epsilon =\frac{c}{a}$.

Jest interesujące, że wszystkie krzywe stożkowe są opisywane tym samym równaniem. Dla elipsy mamy $0\le \epsilon <1$ (zero dla okręgu), dla paraboli $\epsilon =1$, a dla hiperboli $\epsilon >1$. Uniwersalność tego wzoru podkreśla, że rzeczywiście mówimy o krzywych z tej samej rodziny.

Prędkość i energia

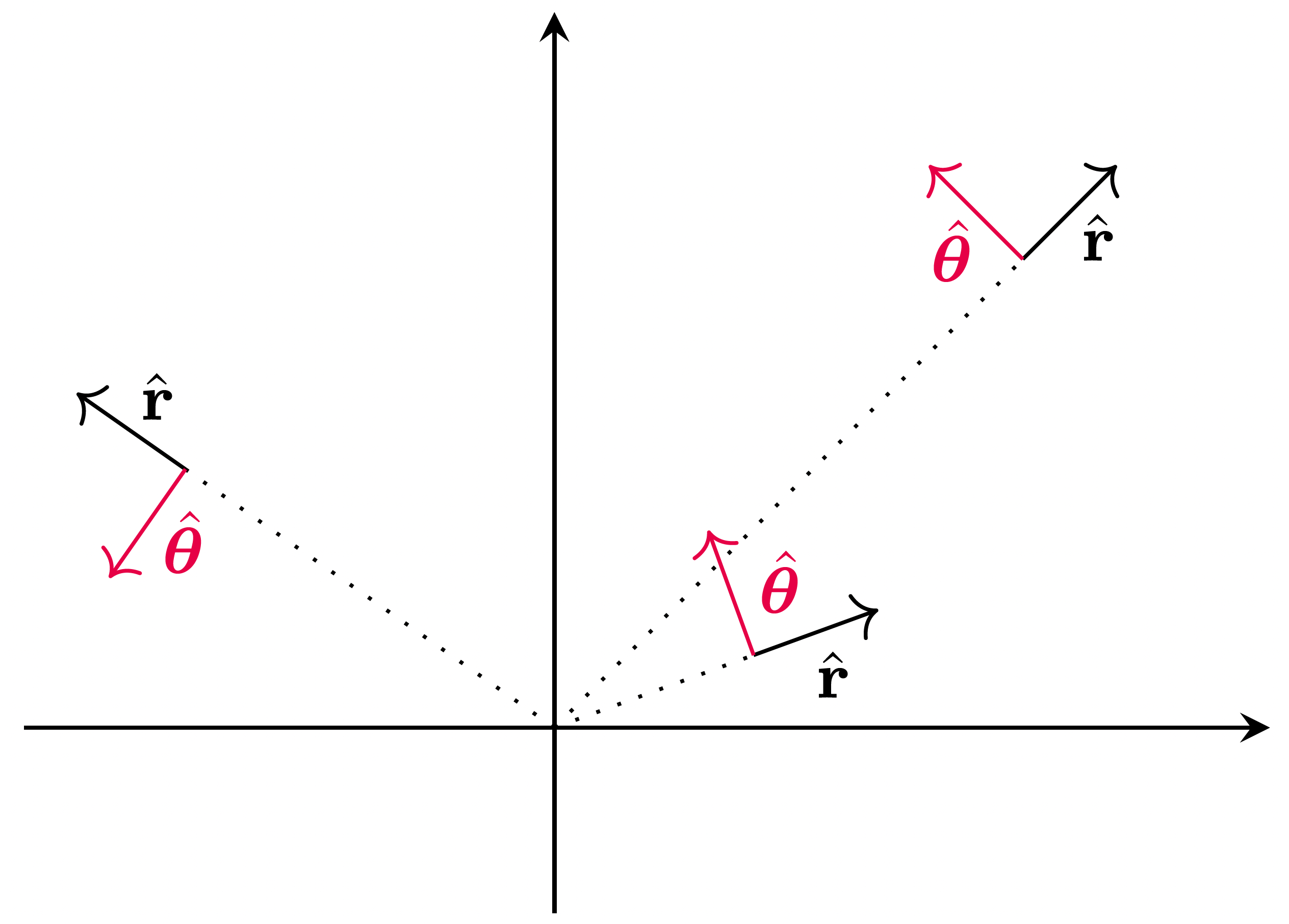
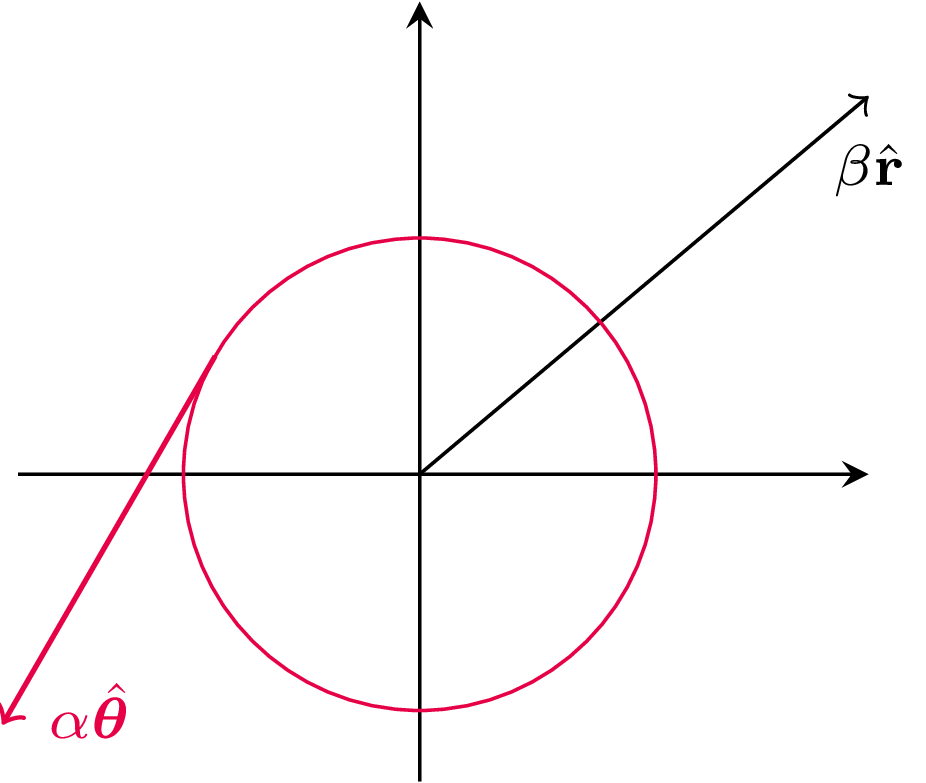
Ponieważ rozważać będziemy sytuację w biegunowym układzie współrzędnych, przypomnijmy, jak najwygodniej opisywać prędkość w tym układzie. W tym celu zdefiniujmy w każdym punkcie płaszczyzny wektory $\hat{\mathbf{r}}$ oraz $\widehat{\theta \theta }$. Wektor $\hat{\mathbf{r}}$ w punkcie $(x,y)$ ma ten sam zwrot co wektor o współrzędnych $(x,y)$, ale długość zawsze równą jeden. Wektor $\widehat{\theta \theta }$ to wektor jednostkowy prostopadły do $\hat{\mathbf{r}}$, co obrazuje rysunek 6. Rozważmy teraz dwa specjalne przypadki ruchu (rys. 7):

1) Ruch wzdłuż półprostej wychodzącej ze środka układu współrzędnych. Ruch jest wciąż w kierunku $\pm \hat{\mathbf{r}}$ i odbywa się z taką szybkością, z jaką zmienia się $r$ – odległość od środka układu współrzędnych. Prędkość w takim ruchu jest zatem równa: $\mathbf{v}=\frac{dr}{dt}\hat{\mathbf{r}}.$

2) Ruch po okręgu o promieniu $r$. Tym razem cały czas poruszamy się w kierunku $\pm \widehat{\theta \theta }$. Szybkość w tym ruchu jest tym większa, im większy jest promień i prędkość kątowa, a zatem $\mathbf{v}=r\frac{d\theta }{dt}\widehat{\theta \theta }.$

Składając te dwa przypadki w jeden i nieco machając rękami, dostajemy ogólny wzór na prędkość: $$\mathbf{v}=\frac{dr}{dt}\hat{\mathbf{r}}+r\frac{d\theta }{dt}\widehat{\theta \theta }.$$ Wynika stąd, że energia kinetyczna dana jest poniższym wzorem (korzystamy tu z faktu, że jednostkowe wektory $\hat{\mathbf{r}}$ oraz $\widehat{\theta \theta }$ są prostopadłe): $$E_K=\frac{1}{2}m|\mathbf{v}{|}^2=\frac{1}{2}m[{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2].$$ Wykorzystamy teraz odkryte przez Keplera prawa ruchu planet do wykazania, że energia kinetyczna planety zależy tylko od jej odległości od Słońca! Jest to zaskakujące, bo okazuje się, że z ogólnego wzoru można w przypadku planet wyrugować zupełnie pochodne czasowe $r$ i $\theta$.

Kepler i Newton

Z trzech praw Keplera, użyjemy dwóch pierwszych:

1) Planety poruszają się po orbitach eliptycznych.
2) Odcinek łączący planetę ze Słońcem wymiata to samo pole w jednakowych przedziałach czasu.

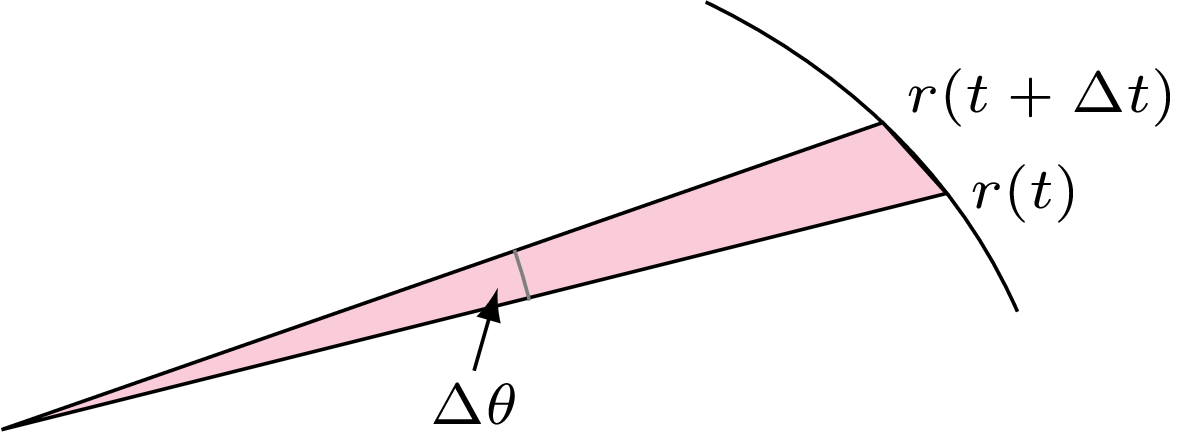
Na początek wykorzystajmy II prawo (o którym można więcej przeczytać w artykule Grzegorza Łukaszewicza i Mikołaja Sierżęgi, ${\mathrm{\Delta }}_{20}^{10}$). Rozpatrzmy moment, gdy planeta w chwili $t$ jest w odległości $r$ od środka układu współrzędnych. Po bardzo krótkim czasie $\mathrm{\Delta }t$ jej odległość od Słońca praktycznie się nie zmieni: $r(t)\approx r(t+\mathrm{\Delta }t)$ (rys. 8), a jej współrzędna kątowa zmieni się o malutkie $\mathrm{\Delta }\theta$. Pole wymiecione w czasie $\mathrm{\Delta }t$ jest więc w przybliżeniu równe polu trójkąta: $$\frac{1}{2}{r}^2\sin (\mathrm{\Delta }\theta )\approx \frac{1}{2}{r}^2\mathrm{\Delta }\theta ,$$ więc po podzieleniu przez $\mathrm{\Delta }t$ i odpowiednim przejściu do granicy otrzymujemy $\frac{1}{2}{r}^2\frac{d\theta }{dt}$ jako prędkość ,,wymiatania pola”. Wynika stąd, że jeśli zdefiniujemy teraz moment pędu: $$L=m{r}^2\frac{d\theta }{dt},$$ to pozostanie on niezmienny w czasie ruchu planety. To dla nas dobra wiadomość, bo pozwala pozbyć się ze wzoru na energię kinetyczną pochodnej kąta $\theta$. Wystarczy tylko podstawić $\frac{d\theta }{dt}=\frac{L}{m{r}^2}$.

Teraz potrzebujemy jeszcze pozbyć się pochodnej: $\frac{dr}{dt}$. W tym celu równanie elipsy zapiszmy w postaci: $$\begin{array}{}\text{(}\star \text{)}& \frac{\alpha }{r}-1=\epsilon \cos \theta \end{array}$$ i zróżniczkujmy obie strony po czasie, dostając prostą zależność miedzy pochodnymi funkcji $r(t)$ i $\theta (t)$: $$-\frac{\alpha }{r^2}\frac{dr}{dt}=-\epsilon \sin \theta \frac{d\theta }{dt}.$$ Po szybkich przekształceniach mamy: $$\frac{dr}{dt}=\frac{\epsilon }{\alpha }{r}^2\frac{d\theta }{dt}\sin \theta =\frac{L\epsilon }{m\alpha }\sin \theta .$$ Wynika stąd, że: $$E_K=\frac{1}{2}m[{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2]=\frac{L^2}{2m}(\frac{{\epsilon }^2}{{\alpha }^2}{\sin }^2\theta +\frac{1}{r^2}).$$ Korzystając z tego, że ${\sin }^2\theta =1-{\cos }^2\theta$ oraz z $(\star )$, dostajemy po zupełnie automatycznych rachunkach: $$\begin{array}{rl}{E}_K& =\frac{L^2}{2m}(\frac{{\epsilon }^2-{\epsilon }^2{\cos }^2\theta }{{\alpha }^2}+\frac{1}{r^2})=\frac{L^2}{2m}(\frac{{\epsilon }^2}{{\alpha }^2}-\frac{1}{{\alpha }^2}{(\frac{\alpha }{r}-1)}^2+\frac{1}{r^2})=\\ & =\frac{L^2}{2m}(\frac{{\epsilon }^2-1}{{\alpha }^2}+\frac{2}{\alpha r})=B+\frac{C}{r}\end{array}$$ dla pewnych stałych $B$ i $C$.

Aby wywnioskować teraz, jaka siła działa na planetę, wystarczy skorzystać z prawa zachowania energii. Energia potencjalna musi być tak dobrana, by jej suma z energią kinetyczną pozostawała stała. Musi więc być równa (z dokładnością do stałej): $$V(r)=-\frac{C}{r}.$$ Siła musi popychać cząstkę/planetę w kierunku najszybszego spadku potencjału, bowiem siła przyspiesza początkowo nieruchome obiekty tak, że zyskują energię kinetyczną – energię potencjalną muszą więc wtedy tracić. Najszybszy spadek potencjału jest w kierunku $-\hat{\mathbf{r}}$. Tempo spadku potencjału w tym kierunku, a więc wielkość siły grawitacyjnej, dostajemy z różniczkowania $V(r)$: $\frac{dV}{dr}=\frac{C}{r^2}$. Stąd siła grawitacyjna działająca na planetę musi być równa: $$\mathbf{F}=-\frac{C}{r^2}\hat{\mathbf{r}}.$$ Otrzymaliśmy zatem słynny wynik Newtona (,,odwrotność kwadratu”!), przebywając całą drogę od cięcia stożka do prawa powszechnego ciążenia. Jest to stan wiedzy z roku 1666.

Wiele ciał

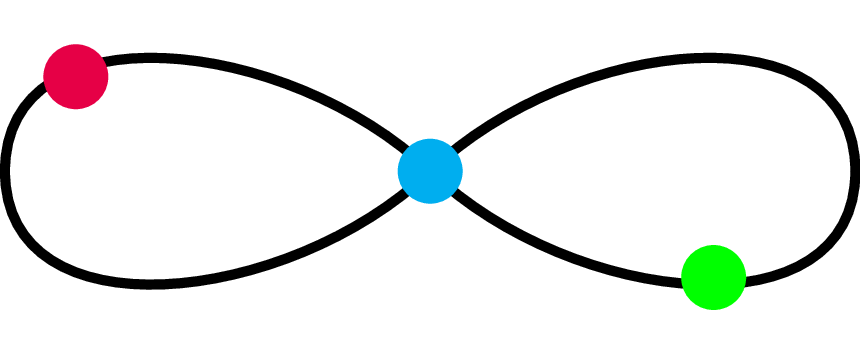
Elegancja i prostota teorii opisującej ruch planety wokół Słońca mogłaby zachęcić nas do tego, byśmy zaczęli szukać podobnych rezultatów opisujących ruch trzech lub więcej ciał niebieskich. Niestety tak uniwersalnych wyników po prostu nie ma. Zagadnienie trzech ciał zazwyczaj prowadzi do chaotycznych trajektorii. W niektórych wyjątkowych przypadkach daje się jednak znaleźć zaskakujące szczególne rozwiązania. Okazuje się na przykład, że przy odpowiednim wyborze warunków początkowych trzy ciała, oddziałujące na siebie tylko grawitacyjnie, mogą podążać za sobą, kreśląc trajektorię ,,ósemki” (rys. 9). Numerycznie zaobserwował to Chris Moore (1993 r.), a w 2000 roku udowodnili to formalnie Richard Montgomery i Alain Chenciner. Ta w gruncie rzeczy ciekawostka zainspirowała niektórych do poszukiwania rozmaitych ,,choreografii”, w których cząstki oddziałujące grawitacyjnie pląsają po specyficznych trajektoriach.

Wiemy też dzisiaj, że w przypadku większej liczby obiektów mogą dziać się jeszcze bardziej dziwne rzeczy. W 1988 roku Jeff Xia pokazał, że można skonstruować taki układ pięciu ciał, w którym cztery ciała krążą po eliptycznych orbitach, a piąte oscyluje między nimi tak, że w skończonym czasie osiąga nieskończoną szybkość, przy czym wszystko to odbywa się bez żadnych zderzeń. Podobny wynik udało się niedawno osiągnąć już dla czterech ciał.

Te publikowane niedawno wyniki, o których tu wspominamy, są ciekawe i pobudzają wyobraźnię, ale są niepomiernie trudniejsze do wyprowadzenia i jednocześnie nie są już tak rewolucyjne, jak genialny wynik Newtona. Cóż, Amerykę odkrywa się tylko raz…