Klub 44

Zadania z matematyki nr 915, 916

Termin nadsyłania rozwiązań: 30 IV 2026

Lista uczestników ligi zadaniowej Klub 44 M

po zakończeniu sezonu (roku szkolnego) 2024/25

Szymon Kitowski-43,92 Barbara Mroczek-43,05 Andrzej Sudoł-42,56 Andrzej Daniluk-2--40,76 Mikołaj Znamierowski-40,68 Marian Łupieżowiec-1--38,54 Krzysztof Kamiński-3--38,09 Roksana Słowik-2--37,51 Michał Adamaszek-9--37,30 Stanisław Bednarek-3--37,24 Jędrzej Biedrzycki-32,29 Błażej Żmija-2--29,84 Mikołaj Pater-4--29,79 Marcin Małogrosz-4--27,82 Piotr Kumor-16--27,28 Janusz Wojtal-26,30 Janusz Fiett-4--25,17 Tomasz Wietecha-15--23,97 Maciej Mostowski-1--22,90 Łukasz Merta-3--22,87 Radosław Kujawa-1--20,21 Andrzej Kurach-4--20,01 Marek Prauza-4--19,57 Norbert Porwol-1--18,50 Paweł Łabędzki-1--18,29 Grzegorz Karpowicz-2--17,90 Janusz Olszewski-25--17,53 Paweł Kubit-8--17,31 Patryk Jaśniewski-1--16,62 Paweł Najman-9--16,42 Bartek Knapik-13,39

Legenda (przykładowo): stan konta 9–37,30 oznacza, że uczestnik już dziewięciokrotnie zdobył 44 punkty, a w kolejnej (dziesiątej) rundzie ma 37,30 punktu.

Zestawienie obejmuje wszystkich uczestników ligi, którzy spełniają następujące dwa warunki:

– stan ich konta (w aktualnie wykonywanej rundzie) wynosi co najmniej 13 punktów;

– przysłali rozwiązanie co najmniej jednego zadania z rocznika 2023, 2024 lub 2025.

Nie drukujemy więc nazwisk tych uczestników, którzy rozstali się z ligą trzy lata temu (lub dawniej); oczywiście jeśli ktokolwiek z nich zdecyduje się wrócić do naszych matematycznych łamigłówek, jego nazwisko automatycznie wróci na listę. Serdecznie zapraszamy!

Redaguje Marcin E. KUCZMA

915. Funkcja parzysta \({f\colon\,\mathbb R\to\mathbb R},\) z wartością \({f(0)=0},\) ma w całym zbiorze \(\mathbb R\) ciągłą pochodną. (a) Udowodnić, że jeśli \(f\) ma w punkcie 0 pochodną drugiego rzędu (skończoną), to istnieją dwa przystające okręgi takie, że początek układu współrzędnych jest jedynym punktem wspólnym wykresu funkcji \(f\) z każdym z tych okręgów. (b) Podać przykład pokazujący, że bez założenia istnienia \(f”(0)\) teza części (a) nie musi zachodzić.

916. Wzdłuż okręgu należy rozmieścić groszki w trzech różnych kolorach; mamy \(k\) groszków jednego koloru, \(l\) groszków drugiego, \(m\) groszków trzeciego koloru. Znaleźć warunek algebraiczny wiążący liczby \(k,l,m,\) konieczny i dostateczny na to, by istniało rozmieszczenie, w którym żadne dwa groszki jednakowego koloru nie sąsiadują.

Zadanie 916 zaproponował pan Paweł Kubit z Krakowa.

907. Oznaczmy tę wspólną wartość przez \(A.\) Mamy równość \((x_k-x_l)A=x_k^{n+1}- x_l^{n+1},\) czyli  \({x_k^{n+1}-Ax_k=x_l^{n+1}-Ax_l}\)  dla każdej pary \({k,l\in\{1,\ldots,m\}},\) \({k\ne{l}}.\) To znaczy, że wyrażenie \({x_k^{n+1}-Ax_k}\) ma jednakową wartość dla wszystkich \({k\in\{1,\ldots,m\}}.\) Oznaczmy ją przez \(C.\) Liczby \(x_1,\ldots,x_m\) są więc różnymi pierwiastkami wielomianu \({W(x)=x^{n+1}-Ax-C}.\) Jego pochodna \({W'(x)=(n+1)x^n-A}\) ma zatem co najmniej \({m-1}\) różnych pierwiastków.

Gdy \(n\) jest liczbą parzystą, wielomian \({(n+1)x^n-A}\) może mieć co najwyżej dwa pierwiastki; stąd oszacowanie \({m\le3}.\) Wartość \({m=3}\) jest osiągalna (na wiele sposobów); na przykład trójka liczb \({(x_1,x_2,x_3)=(-1,0,1)}\) spełnia postawiony warunek (dla każdego parzystego \(n\)).

Gdy \(n\) jest liczbą nieparzystą, wielomian \({(n+1)x^n-A}\) może mieć co najwyżej jeden pierwiastek, więc \({m\le2}\); a dla \({m=2}\) warunek zadania niczego nie żąda. Stąd odpowiedź: szukane maksimum to \({m=3}\) oraz \({m=2}\) odpowiednio dla parzystych i nieparzystych \(n.\)

908. Niech \(a\) będzie jedną z szukanych liczb; jasne, że \({a>1}.\) Rozpatrzmy przypadek, gdy \({a-1}\) ma dzielnik pierwszy \({p>2}.\)

Weźmy dowolną liczbę \({q\in\mathbb N},\) dla której kongruencja \({x^2\equiv{q}}\) (mod p) nie ma rozwiązania (wiadomo, że niereszty kwadratowe istnieją). Niech \({n=\bigl({1\over 2}(p+1)\bigr)^3(q-1)}.\) W myśl warunku zadania istnieje liczba \({j\in\mathbb N}\) taka, że \({{1\over 2}\,j(j+1)=1+a+\ldots+a^{n-1}}.\) Skoro \({a\equiv1},\) zatem \({{1\over 2}\,j(j+1)\equiv{n}\equiv\bigl({1\over 2}\bigr)^3(q-1)}\) (mod \(p\)) i po pomnożeniu przez 8: \[4j(j+1)\equiv q-1,\ \ \ \ \hbox{czyli}\ \ \ \ q\equiv(2j+1)^2\pmod{p},\] wbrew wcześniejszemu wyborowi liczby \(q.\) Rozpatrywany przypadek okazał się niemożliwy.

Pozostaje przypadek, gdy \({a=2^s+1}\) dla pewnego \({s\in\mathbb N\cup\{0\}}.\) Warunek zadania (dla \({n=3}\)) żąda, by \({1+a+a^2={1\over 2}\,j(j+1)}\) dla pewnego \({j\in\mathbb N}.\) Po podstawieniu \({a=2^s+1}\) i prostym przekształceniu dostajemy równanie \[2^{s+1}(2^s+3)=(j-2)(j+3).\] Czynniki po prawej stronie są różnej parzystości, więc jeden z nich dzieli się przez \(2^{s+1}\); stąd (większy z nich) \({j+3\ge2^{s+1}}.\) Drugi jest wtedy dzielnikiem liczby \({2^s+3}\); stąd (mniejszy) \({j-2\le2^s+3}.\) Uzyskane dwustronne oszacowanie \({2^{s+1}-3\le{j}\le2^s+5}\) pociąga nierówność \({2^s\le8}.\) Dla \({s=0,1,2}\) napisane równanie nie jest spełnione dla żadnego \(j.\) To znaczy, że \({s=3},\) czyli \({a=9}.\) Dla \({a=9}\) i dowolnego \(n\) suma dana w zadaniu \({1+9+\ldots+9^{n-1}={1\over 8}\,(3^n-1)(3^n+1)}\) jest liczbą postaci \({{1\over 2}\,j(j+1)}\) dla \({j={1\over 2}(3^n-1)}.\) Stąd odpowiedź: \({a=9}\) jest jedyną liczbą spełniającą postawiony warunek. (Pomysł rozwiązania: Marcin Massalski).

Podsumowanie ligi zadaniowej Klubu 44 M w roku szkolnym 2024/2025

Weterani Klubu 44 M (w kolejności uzyskiwania statusu Weterana):

J. Janowicz (8), P. Kamiński (5), M. Gałecki (5), J. Uryga (4), A. Pawłowski (4), D. Sowizdrzał, T. Rawlik (6), M. Mazur, A. Bonk, K. Serbin, J. Ciach (5), M. Prauza (4), P. Kumor (16), P. Gadziński (7), K. Jedziniak, J. Olszewski (25), L. Skrzypek (4), H. Kornacki, T. Wietecha (15), T. Józefczyk, J. Witkowski (5), W. Bednorz, B. Dyda (5), M. Peczarski, M. Adamaszek (9), P. Kubit (8), J. Cisło (18), W. Bednarek (10), D. Kurpiel, P. Najman (9), M. Kieza (4), M. Kasperski (6), K. Dorobisz, A. Woryna (4), T. Tkocz, Z. Skalik (4), A. Dzedzej, M. Miodek, M. Małogrosz (4), K. Kamiński, J. Fiett (4), M. Spychała (6), A. Kurach (4), S. Bednarek, M. Pater (4), Ł. Merta

(jeśli uczestnik przekroczył barierę 44 punktów więcej niż trzy razy, sygnalizuje to liczba w nawiasie).

Pozostali członkowie Klubu 44 M (alfabetycznie): „dwukrotni”: Z. Bartold, A. Czornik, A. Daniluk, Z. Galias, Ł. Garncarek, J. Garnek, A. Idzik, P. Jędrzejewicz, G. Karpowicz, H. Kasprzak, T. Komorowski, Z. Koza, J. Łazuka, J. Małopolski, K. Maziarz, J. Mikuta, E. Orzechowski, R. Pagacz, K. Patkowski, K. Pióro, F. S. Sikorski, J. Siwy, R. Słowik, S. Solecki, T. Warszawski, P. Wiśniewski, G. Zakrzewski, K. Zygan, B. Żmija; „jednokrotni”: R. M. Ayoush, T. Biegański, W. Boratyński, P. Burdzy, T. Choczewski, M. Czerniakowska, P. Duch, P. Figurny, M. Fiszer, L. Gasiński, A. Gluza, T. Grzesiak, K. Hryniewiecki, K. Jachacy, M. Jastrzębski, P. Jaśniewski, A. Jóźwik, J. Klisowski, J. Kraszewski, A. Krzysztofowicz, R. Kujawa, T. Kulpa, A. Langer, R. Latała, P. Lipiński, P. Lizak, P. Łabędzki, M. Łupieżowiec, W. Maciak, J. Mańdziuk, B. Marczak, M. Marczak, M. Matlęga, K. Matuszewski, R. Mazurek, H. Mikołajczak, M. Mikucki, J. Milczarek, R. Mitraszewski, K. Morawski, M. Mostowski, W. Nadara, W. Olszewski, R. Pikuła, B. Piotrowska, W. Pompe, N. Porwol, M. Roman, M. Rotkiewicz, A. Ruszel, Z. Sewartowski, A. Smolczyk, P. Sobczak, Z. Surduka, T. Szymczyk, W. Szymczyk, W. Tobiś, K. Trautman, P. Wach, M. Warmuz, J. Węgrecki, G. Wiączkowski, K. Witek, A. Wyrwa, M. Zając, Z. Zaus, K. Zawisławski, P. Żmijewski.

Jak co roku – omówienie wybranych zadań, niekoniecznie o parametrach: współczynnik trudności (\(WT\)) wysoki, liczba przysłanych rozwiązań (\(LPR\)) niewielka. Grono uczestników, którzy regularnie przysyłają prace, jest niezwykle stabilne – i są to w większości prace zdecydowanie dobre. Wpływ na wartości wspomnianych parametrów jest oczywisty. Jedyne dwa zadania z wartością \(WT\) około 3 (ciekawostka: oba geometryczne) zawdzięczają ów współczynnik zadaniom im towarzyszącym, może nadmiernie łatwym.

W e-wydaniu, jak zwykle, znajdziemy niektóre prace uczestników oraz ciekawe komentarze (zakładka: „Załącznik do elektronicznego omówienia ligi matematycznej”).

\(*\ \ \ *\ \ \ *\)

\({A,B\in\mathbb R\,\colon\;\exists{u,v,w\in\mathbb C}\,\colon\;|u|=|v|=|w|=1=uvw,\;\;u+v+w=A+Bi}\); \({\min{A}= ?}\) Zadanie nietrudne, sporo dobrych rozwiązań. Ale – uwaga – przy zliczaniu \(LPR\) nie zostały uwzględnione prace, w których zagadnienie zostało sprowadzone do szukania minimalnej wartości pewnej funkcji dwóch zmiennych rzeczywistych przez obliczenie pochodnych cząstkowych i przyrównanie ich (obu) do zera (czyli wyznaczenie punktów krytycznych badanej funkcji) – i pochopna konkluzja, że najmniejsza z wartości w znalezionych punktach to szukane minimum funkcji. W sytuacjach, jakie wynikły w tym zadaniu, uzasadnienie poprawności konkluzji jest łatwe – niemniej niezbędne; jego brak to znacząca usterka.

[Dygresja – pytanie ukazujące potrzebę ostrożności przy podobnych rozumowaniach. Niech np. \({D=\{(x,y)\colon\,x\ge0,\,y\ge0\}}.\) Załóżmy, że funkcja \({f\colon D\to\mathbb R}\) jest ciągła w całym zbiorze \(D,\) ma ciągłe pochodne cząstkowe w punktach wewnętrznych, a najmniejsza z jej wartości w punktach krytycznych wynosi \(m\); ponadto w punktach brzegu zbioru \(D\) przyjmuje tylko wartości \({{}\ge{m}}\) oraz jej wartości wzdłuż każdej półprostej (zawartej w \(D\)) dążą do granicy \({{}\ge{m}}.\) Czy stąd wynika, że \(m\) jest jej najmniejszą wartością? Jako odpowiedź na to pytanie niech posłuży przykład: \({{}\;f(x,y)=x^5-x^3y-x^2y+y^2}.\)]

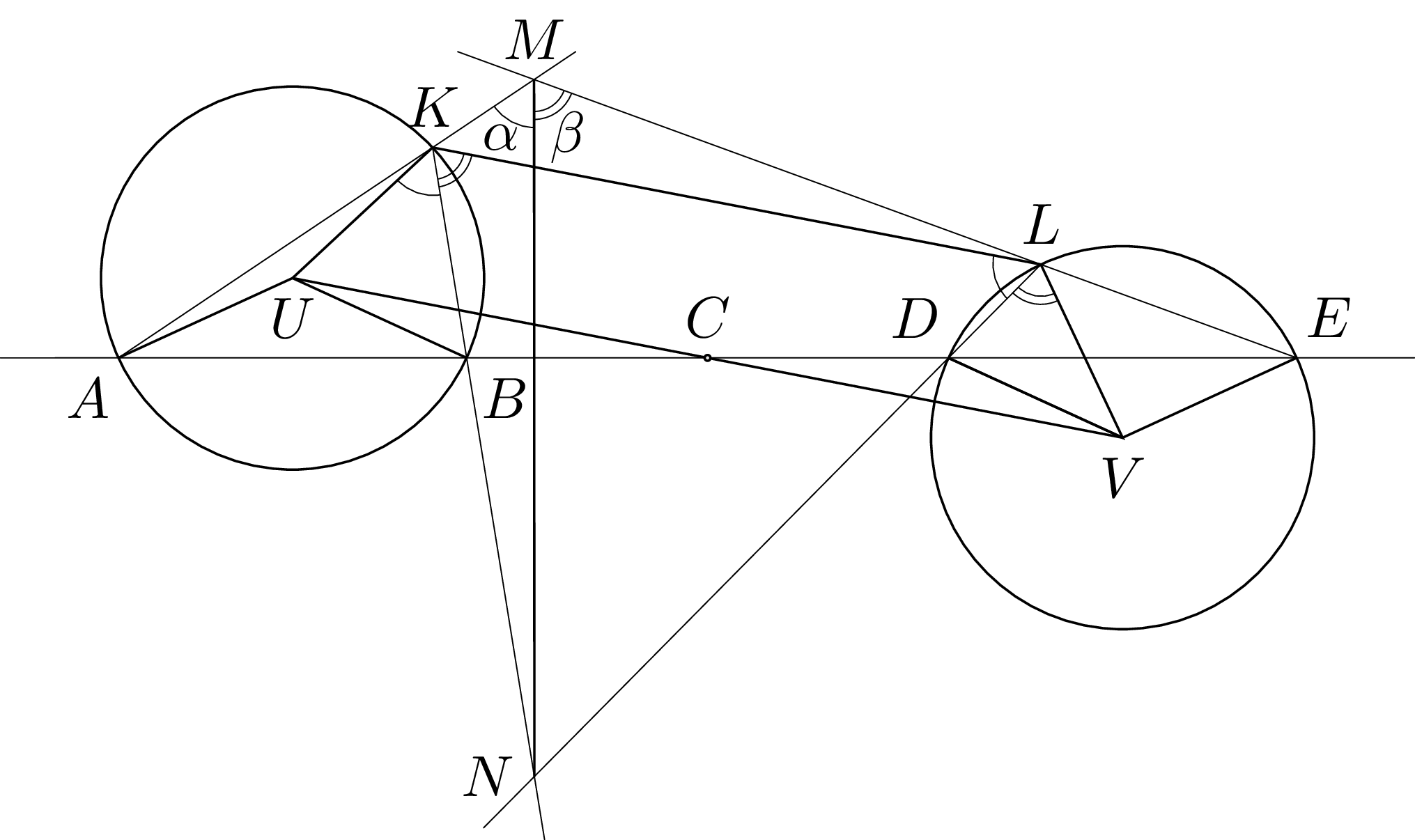
\(A,B,C,D,E\) (kolejno) na prostej, \({CA=CE},\) \({CB=CD}\);  \(K,L\) po jednej jej stronie; kąty ostre: \({\angle{KAB}+\angle{KBA}+\angle{LDE}+\angle{LED}=180^\circ}\);  \({{KB}\cap{LD}=\{N\}},\) \({{AK}\cap{EL}=\{M\}}\);  \({MN\perp{AE}}\); odcinek \(MN\) przecina \(KL\) \(\Rightarrow\) \({CK=CL}\) Większość rozwiązań (M. Adamaszek, A. Kurach, J. Olszewski, M. Pater, M. Znamierowski), podobnie jak firmowe, polegała na wprowadzeniu punktu uzupełniającego trójkąt \(AKE\) (lub \(ALE\)) do równoległoboku. Marek Spychała – nieco inaczej, oryginalnie: z założeń wynikają równości \({AB=DE},\) \({\angle{AKB}+\angle{DLE}=180^\circ},\) a z nich wnioski: czworokąt \(KMLN\) jest cykliczny; okręgi \((AKB)\) i \((DLE)\) mają równe promienie (tw. sinusów); ich środki \(U\) i \(V\) leżą po przeciwnych stronach prostej \(AE\); trójkąty \(AUB\) i \(DVE\) są przystające. Symetria względem punktu \(C,\) która zamienia punkty \(A\) i \(E\) oraz punkty \(B\) i \(D,\) zamienia także punkty \(U\) i \(V.\) Tak więc \(C\) jest środkiem odcinka \(UV.\) Oznaczmy: \({\angle{KMN}=\alpha},\) \({\angle{LMN}=\beta}\); skoro \({MN\perp{AB}},\) zatem \({\angle{BAK}=90^\circ-\alpha},\) skąd \({\angle{UKN}={1\over 2}(180^\circ-2\angle{BAK})=\alpha}.\) Dalej \({\angle{NKL}=\beta}\) (okrąg \(KLMN\)); \({\angle{UKL}=\angle{UKN}+\angle{NKL}=\alpha+\beta}.\) Analogicznie \({\angle{VLK}=\beta+\alpha}.\) Wobec tego czworokąt \(UKLV\) jest trapezem równoramiennym. Punkt \(C\) jest środkiem jego podstawy \(UV\); stąd teza: \({CK=CL}.\)

Dość podobnie, zgrabnie: Barbara Mroczek (\(\to\) e-wydanie). Ponadto dwa rozwiązania rachunkowe (T. Wietecha, P. Wiśniewski).

\({A_n={1\over n}\sum_{k=1}^{2^n}{1\over k}}\) dla \({n\in\mathbb N}\) \(\Rightarrow\) ciąg \((A_n)\) maleje Badanie ciągu o wyrazach \({A_n={1\over n} H(2^n)},\) gdzie \({H(N)=\sum_{k=1}^N{1\over k}\,},\) wręcz zaprasza do wejścia w język analizy (logarytmy, pochodne, całki) – i tak wygląda większość rozwiązań (w tym i ,,firmówka”…). A nie lepiej na poziomie gimnazjum? Popatrzmy (Janusz Olszewski): \[\textstyle H(2^{n+1})-H(2^n)={1\over 2^n+1}+\ldots+{1\over 2^{n+1}}<1\] (bo suma po prawej stronie ma \(2^n\) składników, każdy \({<2^{-n}}\)). Podstawiając \({H(2^n)=nA_n},\) dostajemy nierówność \[\begin{aligned} 0>(n+1)A_{n+1}-nA_n-1 & =(n+1)(A_{n+1}-1)-n(A_n-1)>{} \\ {} & >n(A_{n+1}-1)-n(A_n-1), \end{aligned}\] czyli \({A_{n+1}-1<A_n-1}\): teza!

Autor zadania (Jerzy Cisło) też zaproponował rozwiązanie w podobnym stylu; i nikt ponadto spośród uczestników.

Odnotujmy jeszcze podejście „erudycyjne”, wykorzystujące twierdzenie Younga: \[\textstyle H(n)=\gamma+\ln{n}+{1\over 2(n+\theta_n)}\,,\ \ \ \ 0<\theta_n<1 \tag{Y}\] (\(\gamma\) – stała Eulera); aby uzyskać tezę zadania \({(n+1)H(2^n)>nH(2^{n+1})},\) wystarczy pokazać, że \[\textstyle (n+1)\bigl(\gamma+\ln{2^n}+{1\over 2(2^n+1)}\bigr)>n\bigl(\gamma+\ln{2^{n+1}}+{1\over 2\cdot 2^{n+1}}\bigr),\] czyli że  \({2\gamma>{n\over 2^{n+1}}-{n+1\over 2^n+1}\,},\)  a to oczywiste, bo prawa strona ujemna. Jednak twierdzenie \((Y)\) jest mało znane i niełatwo dostępne (Google wyrzuca kilka innych twierdzeń Younga). Tomasz Wietecha znalazł w pracy arxiv.org/pdf/2204.09226 wynik:  \({H(n)=\gamma+\ln{n}+{1\over 2n}-{1\over 12n^2}+\epsilon_n},\)  \({0<\epsilon_n<{1\over 4n^3}\,},\)  z którego nierówność dwustronna \((Y)\) daje się niezbyt trudno wyprowadzić. Jeszcze jeden z uczestników w ten sam sposób wyprowadził tezę zadania z nierówności \((Y),\) jednak nie podając ani jej dowodu, ani żadnego odsyłacza.

\(ABCD\) –  czworokąt wypukły; obwód \(p,\) przekątne \(m,n\);  \(ABCE\) – równoległobok \(\Rightarrow\) \({DE\le{p-m-n}}\) Traktując punkty jako liczby zespolone i oznaczając \({A-B=x},\) \({B-C=y},\) \({C-D=z},\) rozwiązanie firmowe sprowadzało tezę zadania do nierówności \[|x|+|y|+|z|+|x+y+z|\ge|x+y|+|y+z|+|z+x|\] (dalej dając jej dowód). Redaktor Ligi nie miał świadomości – jaką mieli liczni uczestnicy – że ta nierówność jest dość dobrze znana jako Hlawka inequality (lub: Hornisch–Hlawka) i zachodzi nie tylko dla liczb \({x,y,z\in\mathbb C},\) ale dla dowolnych wektorów w przestrzeni liniowej unormowanej, z normą określoną przez iloczyn skalarny. Jak wielokrotnie bywało, popis erudycji dał Piotr Kumor; całość jego pracy w e-wydaniu – znajdziemy tam obszerne rozważania, odsyłacze do literatury (nawet reprodukcje fragmentów prac), dyskusje przypadków równości, kwestie istotności założeń (w różnych wariantach twierdzenia) itp. Janusz Olszewski (\(\to\) e-wydanie) przysłał trzy sposoby, w tym odsyłacz do Hlawki (z komentarzem).

\(f_1,f_2,f_3,f_4\) – wielomiany rzeczywiste; \({{f_1}\le{f_2}\le{f_3}\le{f_4}}\) w \([0,1]\); \({{f_2}\le{f_4}\le{f_1}\le{f_3}}\) w \([-1,0]\) \(\Rightarrow\) \({f_1=f_2=f_3=f_4}\) Znów: podejście typowe – przez porównanie relacji asymptotycznych (przy 0) funkcji \(f_i\) – ustępowało prostotą wykorzystaniu zwykłej szkolnej algebry: wyrazy wolne \({a_i=f_i(0)}\) spełniają warunki \({{a_1}\le{a_2}\le{a_3}\le{a_4}}\) oraz \({{a_2}\le{a_4}\le{a_1}\le{a_3}},\) więc są równe (oznaczmy ich wspólną wartość przez \(a\)); zatem istnieją wielomiany \(g_i\) takie, że \({f_i(x)=a+xg_i(x)}\) (\({i=1,2,3,4}\)); w przedziale \((0,1]\) spełniają one nierówności takie jak funkcje \(f_i,\) zaś w \([-1,0)\) – przeciwne; stąd ich wyrazy wolne \({b_i=g_i(0)}\) spełniają warunki \({{b_1}\le{b_2}\le{b_3}\le{b_4}}\) oraz \({{b_3}\le{b_1}\le{b_4}\le{b_2}},\) więc są równe (wspólna wartość \(b\)); i dalej: istnieją wielomiany \(h_i\) takie, że \({g_i(x)=b+xh_i(x)},\) spełniające w przedziale \((0,1]\) nierówności takie jak \(g_i,\) zaś w \([-1,0)\) przeciwne, czyli takie jak \(f_i,\) wobec czego wartości \({c_i=h_i(0)}\) spełniają warunki takie jak \(a_i,\) więc znów są równe; pozostaje zauważyć, że \(b_i\) to wpółczynniki wielomianów \(f_i\) przy \(x\); dalej: \(c_i\) to wpółczynniki \(f_i\) przy \(x^2\); kontynuując to rozumowanie (indukcja), wykazujemy, że w wielomianach \(f_i\) współczynniki przy zmiennej w jednakowej potędze są równe, co oznacza, że te wielomiany są równe.

Obie metody były reprezentowane w przysłanych pracach; ta pierwsza (przez asymptotykę) bardziej licznie; ciężko dokładnie ocenić, bo niektóre rozwiązania zawierały elementy jednej i drugiej metody.

Dla \({n\in\mathbb N}\):  \({w(n)=\max\{w\colon\;10^{-w}n!\in\mathbb N\}},\)  \({10^{-w(n)}n!=\colon\,f(n)}\) \(\Longrightarrow\) \({\forall{m\in\mathbb N}\colon\;f(5^m)\equiv2^m}\) (mod\(\,5\)) Przez dość długi czas nie mogliśmy się zdecydować, czy chcemy włączyć to zadanie do Ligi. Przecież ostatnia niezerowa cyfra liczby \(n!\,\) to hasło często spotykane – musi być w sieci. I jest – tylko że wszystko, co wyskakuje, to proste przykłady, dla konkretnych wartości \(n\) – nie ogólne twierdzenie, które byłoby tu przydatne; trzeba poszperać głębiej. Paweł Kubit, jako jedyny, dotarł do formuły \[L(n!)=LD(2^aL(a!)L(b!))\ \ \ \ \hbox{dla}\ n=5a+b,\] w której \(LD(m)\) to ostatnia cyfra liczby \(m\);  \(L(n!)\) to \(LD(f(n))\) (gdzie \(f\) to funkcja z zadania). Podał dwa źródła, z których jedno nie zawiera dowodu (tylko przykłady), zaś drugie  www.geeksforgeeks.org/dsa/last-non-zero-digit-factorial  odsyła do kolejnego materiału, w którym faktycznie jest dowód (formuły nawet bardziej ogólnej), wszelako ciężki do przebrnięcia – tę ścieżkę (wraz z wyjaśnieniem, jak owa formuła prowadzi do tezy naszego zadania) proponujemy entuzjastom. Jednak prościej jest zwyczajnie zrobić zadanie – niezbyt przecież trudne (jak wskazuje wartość \(LPR\)).

Wszyscy pozostali uczestnicy przysłali prace różniące się w detalach, ale bazujące na jednej koncepcji, by w iloczynie definiującym \(n!\) wydzielić wszystkie potęgi piątki, a pozostałe czynniki pogrupować w bloki czteroelementowe. Jedyna trudność polegała na tym, jak tu zgrabnie zapisać rozumowanie, które w myśli jawi się jako całkiem jasne. Szczyt zwięzłości, przy jednoczesnej klarowności przekazu, osiągnął Jerzy Cisło (\(\to\) e-wydanie)!

Zadania z fizyki nr 812, 813 Termin nadsyłania rozwiązań: 30 IV 2026

Redaguje Elżbieta ZAWISTOWSKA

812. Na drewnianą pochylnię tworzącą kąt \(\alpha\) z poziomem wciągana jest za pomocą sznurka skrzynia. Współczynnik tarcia skrzyni o pochylnię wynosi \(\mu\). Pod jakim kątem do poziomu należy skierować sznurek, aby z najmniejszym wysiłkiem wciągać skrzynię z zadanym przyspieszeniem \(a\)?

813. Dwie cząstki o masach \(m\) i \(M\) oraz ładunkach o jednakowych wartościach bezwzględnych, ale przeciwnych znakach, poruszają się po okręgach pod wpływem przyciągania elektrycznego. Wartość prędkości cząstki o masie \(m\) momentalnie zwiększono, nie zmieniając przy tym kierunku prędkości. Ile razy co najmniej wzrosła ta wartość, jeżeli w wyniku tego cząstki rozleciały się na nieskończoną odległość od siebie?

Czołówka ligi zadaniowej Klub 44 F
po zakończeniu roku szkolnego 2024/25 i sprawdzeniu zadań
800 (\(WT=2{,}55\)), 801 (\(WT=2{,}25\)) z numeru 6/2024

Jacek KoniecznyPoznań41,41 Jan ZambrzyckiBiałystok4–39,07 Ryszard WoźniakKraków34,00 Andrzej NowogrodzkiChocianów3–32,28 Paweł PerkowskiOżarów Maz.6–29,93 Krzysztof ZyganLubin26,89 Tomasz WietechaTarnów18–21,64 Paweł KubitKraków20,30 Marian ŁupieżowiecGliwice3–14,49 Krzysztof MagieraŁosiów4–13,42 Zbigniew GaliasKraków1–12,77

Lista obejmuje uczestników ligi, których stan konta wynosi przynajmniej 10 punktów i którzy przysłali rozwiązanie co najmniej jednego zadania z rocznika 2023, 2024 lub 2025.

Rozwiązania zadań z numeru 10/2025

Przypominamy treść zadań:

804. Chłopiec znajduje się w punkcie \(A\) na brzegu rzeki, której prędkość nurtu wynosi \(w\) (rys. 1). Chłopiec może biec po brzegu z prędkością \(v\) i płynąć rzeką z prędkością \(u\) względem wody, przy czym \(u<v.\) W jakiej odległości od punktu \(A\) znajduje się na brzegu punkt \(C,\) z którego chłopiec powinien zacząć płynąć, aby dotrzeć do punktu \(B\) w najkrótszym czasie? Odległość \(|BD|\) punktu \(B\) od brzegu wynosi \(h,\) odległość \(|AD|\) jest równa \(l.\)

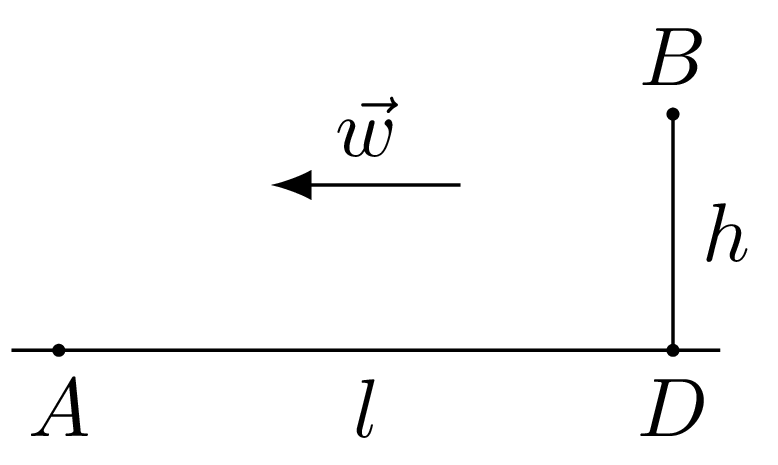Rys. 1

805. Para jednakowych małych kulek \(A\) i \(B\) połączonych nieważką nicią o długości \(l\) zaczyna ześlizgiwać się z gładkiego stołu o wysokości \(l,\) przy czym w chwili początkowej kulka \(B\) znajduje się na wysokości \(h=2l/3\) nad podłogą (rys. 2). Po dotknięciu podłogi kulka \(B\) przykleja się do niej, a kulka \(A\) spada w tym momencie ze stołu. Od jakiej wysokości kulki \(A\) nad podłogą nić będzie napięta?

   

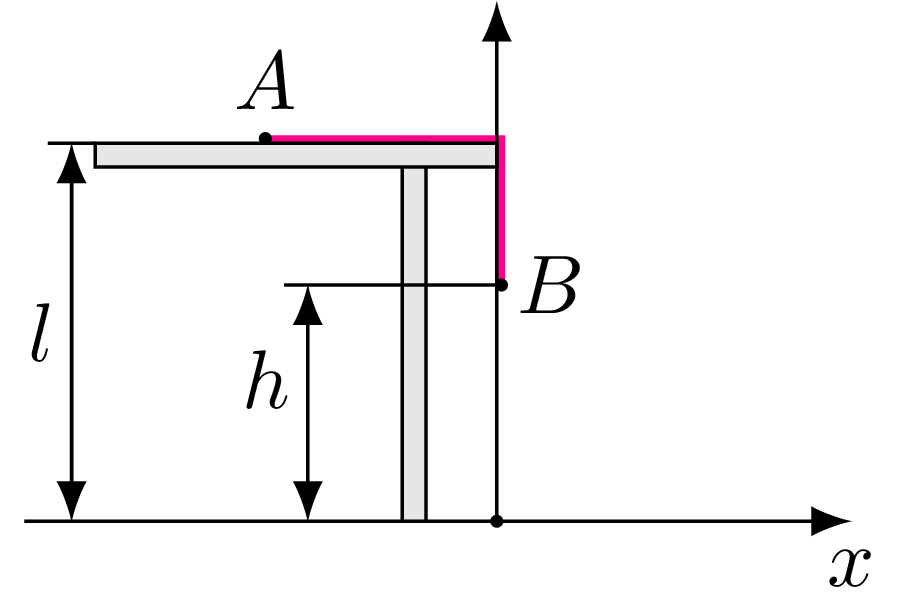Rys. 2

804. Posłużymy się analogią z załamaniem fali na granicy dwóch ośrodków, co zgodnie z zasadą Fermata gwarantuje minimum czasu dotarcia odpowiedniego promienia do punktu B. Warunek dotarcia tego promienia do punktu B zastąpimy warunkiem dotarcia odpowiedniego frontu falowego do tego punktu. Najpierw rozważymy prostszy przypadek nieruchomej wody, np. brzeg jeziora.

Przypadek \(w = 0\) (rysunek poniżej):

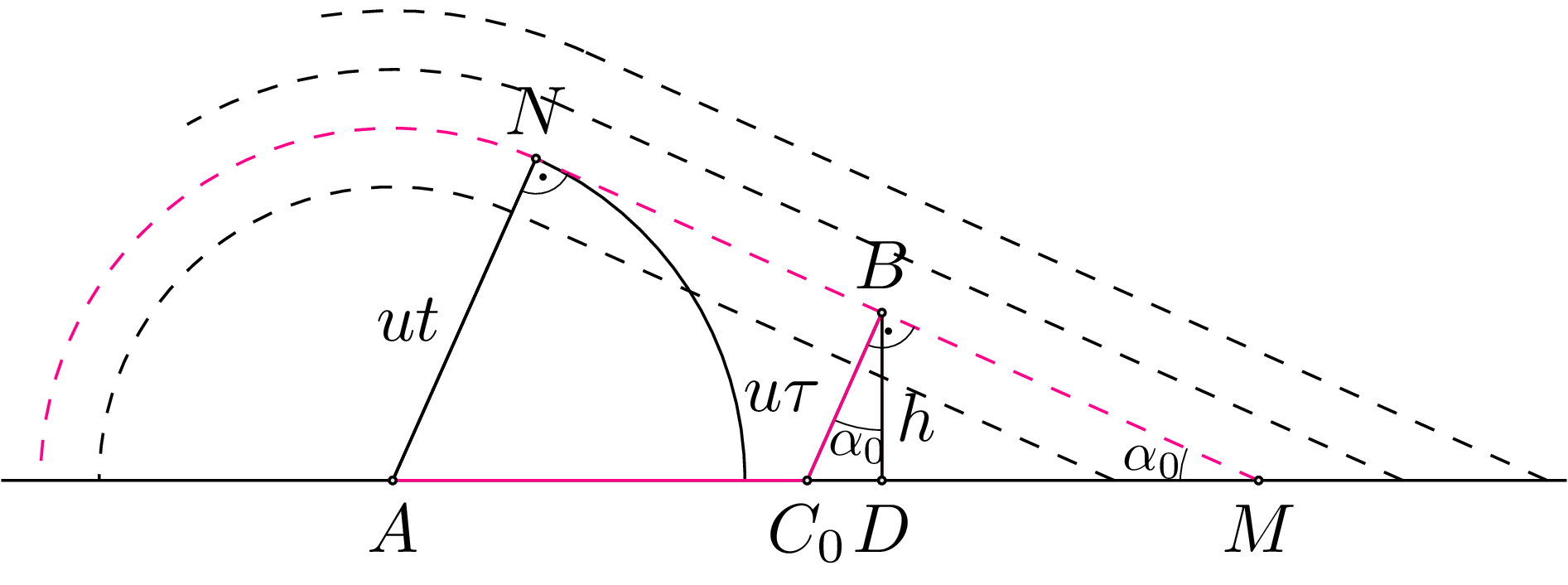Dany front falowy jest jednocześnie zbiorem punktów, do których może dotrzeć chłopiec w zadanym czasie, zaczynając płynąć z różnych punktów na brzegu. Zaznaczony kolorem czerwonym front, docierający do punktu B w minimalnym czasie \(t\), odpowiada promieniowi załamanemu w punkcie \(C_{0}\), który pokrywa się z optymalną trajektorią chłopca \(AC_{0}B\).

Front falowy \(NM\) jest, zgodnie z zasadą Huygensa, obwiednią fal kulistych wychodzących z różnych punktów wejścia chłopca do wody na odcinku \(|AM| = vt\), czyli jest styczną do okręgu o promieniu \(ut\) i środku \(A\) poprowadzoną z punktu \(M\). Z trójkąta \(ANM\) mamy: \[\sin\alpha_{0} = \ {ut\over vt} = {u\over v} = {{\sin\alpha}_{0}\over\sin 90^{\circ}},\] zgodnie z prawem załamania. Ponieważ \(h\)tg\(\propto_{0} = hu/\sqrt{v^{2} - u^{2}}\), więc odległość punktu \(C_{0}\) od punktu \(A\) wynosi: \[\left| AC_{0} \right| = |AD| - \left| C_{0}D \right| = l - hu/\sqrt{v^{2} - u^{2}}.\] Przypadek \(w \neq 0\) (rysunek poniżej):

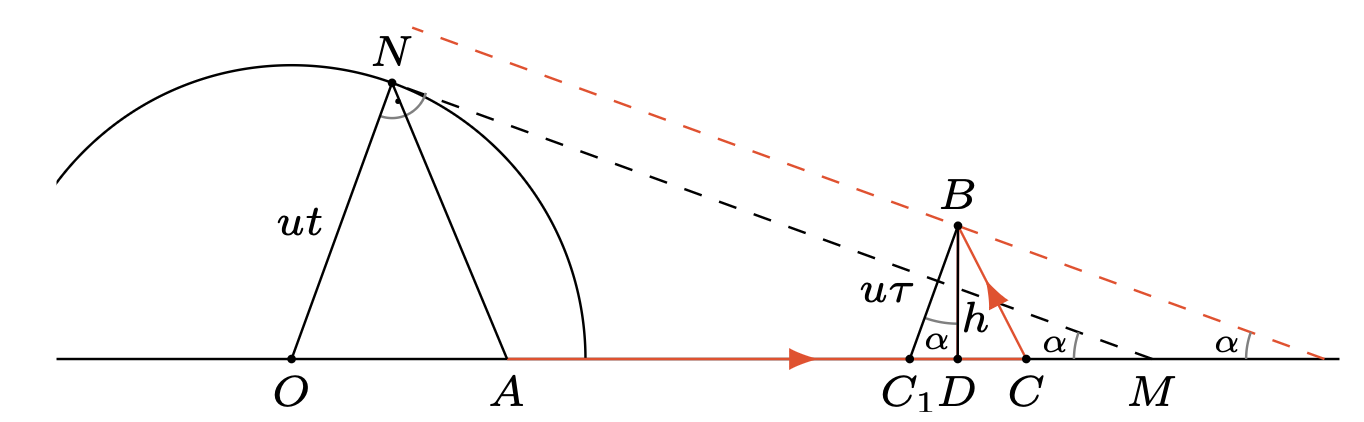Skorzystamy z wyników dla nieruchomej wody i uwzględnimy unoszenie z prądem rzeki względem brzegu. Promień \(ut\) względem nieruchomej wody musi wystartować z punktu \(O\) przesuniętego w lewo względem punktu \(A\) o odcinek o długości \(|OA| = wt\), który pokonała woda w czasie \(t\). Położenie punktu \(M\) nie zmienia się, gdyż nie zależy od prędkości prądu rzeki: \(|AM| = vt\). Styczna \(MN\) wyznacza nachylenie względem brzegu frontów falowych. Z trójkąta \(ONM\) mamy \({\sin\alpha = u/(w + v)}\). Front \(NM\) nie dociera do punktu \(B\) w czasie \(t\). Czyni to następny front, zaznaczony kolorem czerwonym, nachylony do brzegu pod tym samym kątem \(\alpha\). Temu frontowi odpowiada optymalna trajektoria chłopca \(ACB\) względem brzegu, zaznaczona kolorem czerwonym, oraz załamany promień \(u\tau\), względem nieruchomej wody, wychodzący z punktu \(C_{1}\). Punkt  \(C_{1}\) jest przesunięty w prawo względem \(C_{0}\), bo \(\alpha < \alpha_{0}\) . Punkt \(C\) jest przesunięty w prawo względem \(C_{1}\) o odcinek \(\left| C_{1}C \right| = w\tau\), który pokonała woda w czasie płynięcia chłopca, \(\tau\). Ponieważ \({|DC| = \left| C_{1}C \right| - \left| C_{1}D \right| = w\tau - h\tan\alpha}\), a z trójkąta \(C_{1}BD\) mamy \(\cos\alpha = h/u\tau\), skąd czas płynięcia: \[\tau = h/(u\cos\alpha)=\textstyle h(w + v)/\bigl(u\sqrt{(w + v)^{2} - u^{2}}\bigr),\]

więc odległość punktu \(C\) od punktu \(A\) wynosi \[\begin{aligned} |AC| & = |AD| + |DC| = l + w\tau - h\tan\alpha \\&= l + \textstyle h(w^{2} - u^{2} + wv)/\bigl(u\sqrt{(w + v)^{2} - u^{2}}\bigr). \end{aligned}\]

805. Zgodnie z zasadą zachowania energii prędkość kulki \(A\) w chwili ześlizgiwania się ze stołu wynosi \[v_{0} = \sqrt{2gl/3}.\] Po ześlizgnięciu się ze stołu kulka \(A\) porusza się po paraboli, dopóki nić nie jest napięta. Wprowadzając układ współrzędnych, jak na rysunku 2, możemy zapisać współrzędne kulki w chwili \(t\): \[x = v_{0}t,\ \ \ y = l - gt^{2}/2.\] Nić ponownie stanie się naciągnięta, gdy odległość \(|BA|\) zrówna się z długością nici: \[x^{2} + y^{2} = l^{2}.\] Podstawiając współrzędne (2) i uwzględniając (1), otrzymujemy równanie: \[gt^{2}\left( gt^{2}/4 - l/3 \right) = 0.\] Z niego znajdujemy chwilę czasu, w której nić ponownie zostanie napięta: \(t^{2} = 4l/(3g)\) (pierwiastek \(t = 0\) odpowiada chwili ześlizgiwania się ciężarka \(A\) ze stołu). Korzystając z drugiego z równań (2), otrzymujemy szukaną wysokość: \[y = l/3.\]

Podsumowanie ligi zadaniowej Klub 44 F w roku szkolnym 2024/2025 po 801 zadaniach.

Zaskakująco wysoki okazał się współczynnik trudności zadania 794 (\(WT = 3,\)7) z optyki falowej. Z soczewki skupiającej wycięto wąski środkowy pasek, a pozostałe części złożono ze sobą. Na osi optycznej przed soczewką w odległości większej niż ogniskowa umieszczono punktowe źródło światła monochromatycznego. Należało znaleźć maksymalną liczbę prążków interferencyjnych, jaka może powstać na ekranie za soczewką. Właściwe podejście do tego zadania, czyli badanie interferencji światła z obrazów źródła od dwóch części soczewki, zaprezentował jedynie Tomasz Wietecha. Niestety zaraz na początku rozwiązania pomylił (zapewne przez roztargnienie) promienie biegnące z różnych części soczewki.

Drugie miejsce pod względem współczynnika trudności zajęło zadanie 783 (\(WT = 3,\)45). Mała naładowana kulka, zawieszona na nici w jednorodnym polu magnetycznym skierowanym pionowo, została odchylona o mały kąt z położenia równowagi i puszczona swobodnie. Należało znaleźć czas, po którym płaszczyzna wahań obróci się o kąt \(2\pi\). Wymagało to dość żmudnych rachunków. W rozwiązaniu firmowym problem ten uproszczono, korzystając z superpozycji rozwiązań liniowych. Konrad Kapcia zauważył, że równania są analogiczne do równań ruchu wahadła Foucaulta, i korzystając z zacytowanej literatury na ten temat, otrzymał poprawny wynik. Tomasz Wietecha samodzielnie rozwiązał te równania. Zmienił wprawdzie warunki początkowe, co wpływa na kształt trajektorii, jaką zakreśla kulka w płaszczyźnie poziomej, ale nie zmienia wyniku zadania.

Zadanie 787 (\(WT = 3,\)25) z termodynamiki polegało na znalezieniu stanu równowagi w izolowanym cieplnie naczyniu wypełnionym helem i połączonym małymi otworkami z dwiema objętościami również zawierającymi hel, w których utrzymywano stałe ciśnienie i różne temperatury. Autorem jedynego poprawnego rozwiązania jest Krzysztof Zygan.

Zadanie 792 (\(WT = 3,\)23) również wymagało zastosowania metod statystycznych. W pionowym cylindrze zamkniętym od góry tłokiem poruszały się chaotycznie kulki ze znaną średnią prędkością kwadratową. Tłok zaczęto podnosić z zadaną stałą prędkością i zatrzymano na dwa razy większej wysokości. Należało znaleźć średnią prędkość ustaloną po długim czasie, nie uwzględniając strat energii podczas zderzeń oraz sił grawitacji. W pełni poprawne rozwiązanie nadesłał Paweł Perkowski.

W zadaniu 799 (\(WT = 3,\)01) z elektromagnetyzmu elektron krążył po orbicie kołowej w jednorodnym polu magnetycznym. Indukcja pola magnetycznego wzrosła powoli trzy razy, w czasie przewyższającym wielokrotnie okres obrotu. Należało odpowiedzieć, ile zmienił się w tym czasie promień orbity. Ponieważ zmiana pola była bardzo powolna, można było przyjąć, że mimo zmiany pola magnetycznego, a co za tym idzie prędkości i promienia, tor elektronu w czasie jednego okresu pozostaje w przybliżeniu kołowy. Nie było natomiast uzasadnione założenie, jakie przyjęła większość autorów rozwiązań, że prędkość elektronu nie zmienia się. Maksymalną ocenę za to zadanie otrzymał Krzysztof Zygan, który skorzystał z faktu, że dipolowy moment magnetyczny naładowanej cząstki w wolno zmieniającym się polu magnetycznym jest zachowany (podał odnośnik do literatury), i otrzymał poprawny wynik.

W zadaniu 785 (\(WT = 3,\)00) z elektrostatyki kondensator płaski podłączony do źródła napięcia znajdował się w jednorodnym polu elektrycznym, którego linie były prostopadłe do okładek kondensatora. Trzeba było obliczyć pracę, jaką należy wykonać, aby obrócić ten kondensator o kąt \(\pi\) wokół osi prostopadłej do linii zewnętrznego pola elektrycznego. Paweł Perkowski nadesłał rozwiązanie takie jak firmowe, pozostali autorzy rozwiązali inne zadanie, gdy kondensator nie jest podłączony do źródła.

Nikt nie rozwiązał do końca poprawnie zadania 784 (\(WT= 2,\)6) z optyki geometrycznej. Szklany pryzmat o małym kącie łamiącym umieszczono w pewnej odległości od soczewki skupiającej tak, że jedna z jego ścian była prostopadła do osi optycznej soczewki. Po drugiej stronie soczewki w jej ognisku umieszczono punktowe źródło światła. Po przejściu światła przez soczewkę, odbiciu od ścianek pryzmatu i ponownym przejściu przez soczewkę powstawały dwa obrazy w znanej odległości od siebie. Należało znaleźć współczynnik załamania szkła, z którego wykonano pryzmat. Zadanie nie było trudne, ale autorzy rozwiązań ograniczyli się do rozważenia jednego przypadku ustawienia pryzmatu, gdy prostopadła do osi optycznej ścianka pryzmatu była bliższa soczewki.

Paweł Perkowski jest autorem 9 rozwiązań, które uzyskały maksymalną ocenę, drugie miejsce zajmuje Tomasz Wietecha (7), trzecie Krzysztof Zygan (6).

W omawianym roku Tomasz Wietecha po raz osiemnasty (!) przekroczył próg 44 punktów, Konrad Kapcia po raz trzeci.

Cieszy, że dwaj panowie po paru latach przestoju odnowili swój kontakt z Klubem 44 F, martwi śladowy udział uczniów szkół średnich, mimo że rozwiązanie zdecydowanej większości zadań nie wymaga zaawansowanej matematyki.