24 września 2024, podczas odbywającego się w Warszawie IX Dnia Popularyzacji Matematyki, miał miejsce finał 47. Konkursu Uczniowskich Prac z Matematyki im. Pawła Domańskiego. Na tegoroczny Konkurs wpłynęło 8 prac, z których 5 dostało się do finału. Po wysłuchaniu finałowych prezentacji i dyskusji Jury w składzie: Adam Gregosiewicz, Andrzej Komisarski – przewodniczący Jury, Zdzisław Pogoda, Łukasz Rajkowski, Daniel Strzelecki, postanowiło nagrodzić wszystkie prace finałowe.
Złote medale i nagrody w wysokości po 1600 złotych otrzymali:
- Kazimierz Chomicz, uczeń I LO im. Bolesława Chrobrego w Piotrkowie Trybunalskim, autor pracy On the fourth power level of p-adic completions of biquadratic number fields , napisanej pod opieką Tomasza Kowalczyka;
- Franciszek Hansdorfer, uczeń XIV LO im. Stanisława Staszica w Warszawie, autor pracy Aproksymacje p-adyczne , napisanej pod opieką Mariusza Skałby;
- Miłosz Płatek, uczeń V LO im. Augusta Witkowskiego w Krakowie, autor pracy Dowód uogólnionego twierdzenia Sawayamy-Thébault’a , napisanej pod opieką Dominika Burka.
Brązowy medal i nagrodę w wysokości 800 złotych otrzymał Grzegorz Lis, uczeń XX LO im. Leopolda Staffa w Krakowie, autor pracy Nietypowe transformacje geometryczne, napisanej pod opieką Bronisława Pabicha.
Wyróżnienie i nagrodę w wysokości 400 złotych otrzymała Patrycja Lamparska, uczennica XXIV Liceum Ogólnokształcące im. Marii Skłodowskiej-Curie w Łodzi, autorka pracy Matematyka wyboru, napisanej pod opieką Stanisława Goldsteina.
Wszyscy tegoroczni złoci medaliści byli już nagrodzeni podczas wcześniejszych edycji Konkursu. Kazimierz Chomicz i Miłosz Płatek zdobyli odpowiednio brązowy i złoty medal w 46. KUPzM, zaś Franciszek Hansdorfer, brązowy medal w 45. KUPzM.
Tematyka prac Kazimierza Chomicza i Franciszka Hansdorfera leży na pograniczu algebry i teorii liczb. Obie dotyczą tzw. uzupełnień \(p\)-adycznych ciał liczbowych. Są to obiekty algebraiczne mające istotne związki z teorią liczb. Zbieżność tematyki obu prac jest przypadkowa, a uczniowie zajmowali się nieco innymi zagadnieniami. Kazimierz Chomicz badał, ile co najmniej czwartych potęg elementów uzupełnienia \(p\)-adycznego dwukwadratowego rozszerzenia ciała liczb wymiernych trzeba dodać, by uzyskać sumę \(-1.\) Uzyskane przez niego wyniki stanowią zakończoną sukcesem kontynuację badań, które utknęły około 40 lat temu.
Z kolei praca Franciszka Hansdorfera poruszała wiele drobniejszych zagadnień, wśród których znalazła się między innymi efektywna metoda wyznaczania w ciele \(p\)-adycznym pierwiastków kwadratowych niektórych liczb naturalnych, a także użycie liczb \(p\)-adycznych do znajdowania kongruencji takich jak \(7^{43^n}+6^{43^n}+42^{43^n}+36^{43^n}+37^{43^n}\equiv-1\mod 43^{n+1}.\)
Ze względu na złożoność tematu nie opiszemy szczegółowo wyników obu prac. Dość powiedzieć, że istotną część finałowego wystąpienia Kazimierza Chomicza musiało zająć wyjaśnienie poszczególnych słów występujących w tytule jego pracy.
Miłosz Płatek udowodnił tytułowe uogólnienie twierdzenia Sawayamy–Thébaulta, które stanowiło nierozstrzygniętą przez około 10 lat hipotezę. Twierdzenie to głosi, że w sytuacjach przedstawionych na poniższych rysunkach, jeśli trójkąt \(ABC\) oraz okrąg o środku \(O_a\) są ustalone, zaś punkt \(P\) porusza się po dowolnej prostej, wówczas wszystkie uzyskane położenia prostej \(O_1O_2\) przechodzą przez jeden punkt (na rysunkach jest to punkt \(I'\)).
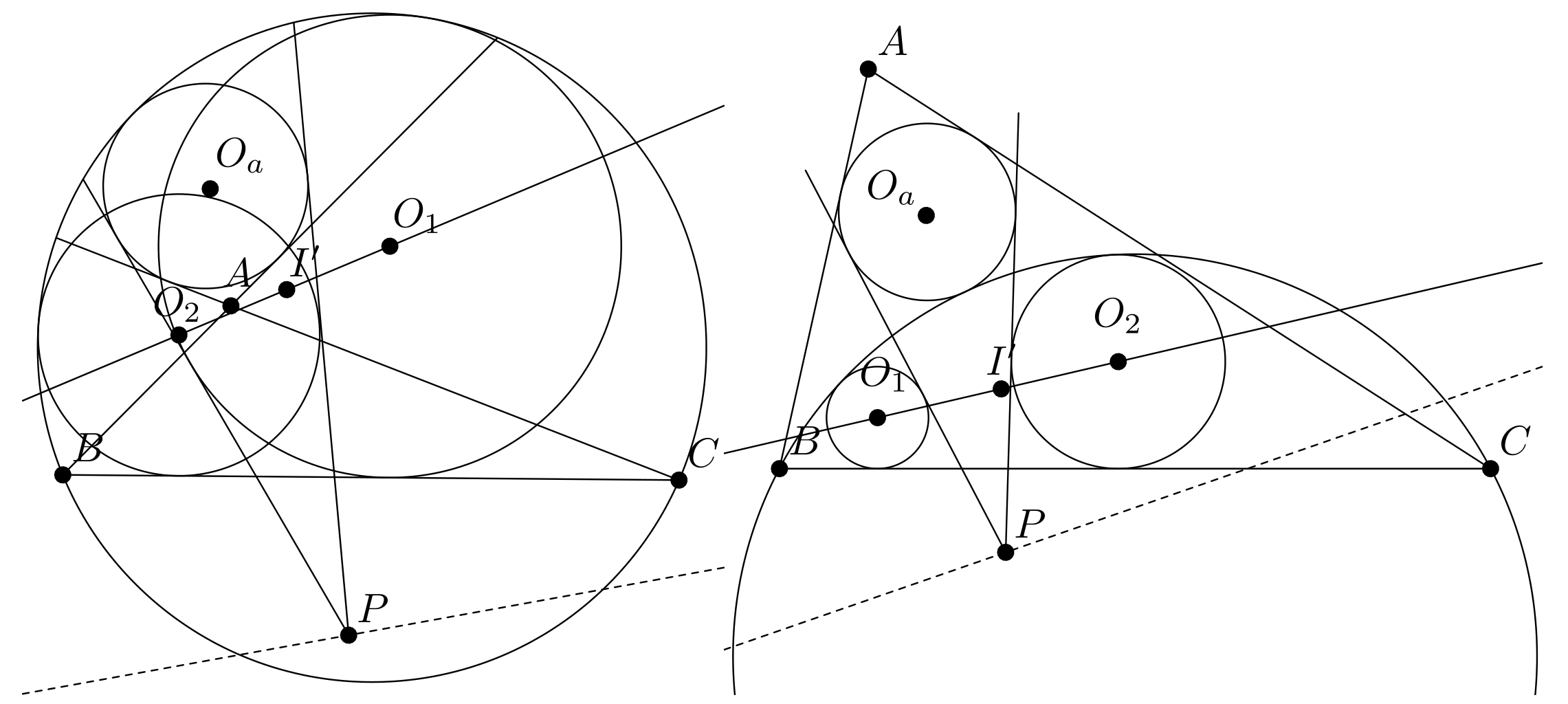
Praca Grzegorza Lisa podzielona jest na trzy części. W pierwszej opisuje, jak można narysować wykres funkcji nie w prostokątnym układzie współrzędnym, lecz w układzie krzywoliniowym, którego oś odciętych stanowi dowolna krzywa gładka. W drugiej części autor uogólnia inwersję względem okręgu, definiując inwersję względem dowolnej krzywej ograniczającej obszar wypukły, takiej jak elipsa, trójkąt i inne wielokąty. W ostatniej części rozważane są obroty względem elipsy i paraboli. Różnią się one od zwykłych obrotów tym, że obracające się punkty poruszają się nie po okręgach, lecz po elipsach lub parabolach. Wszystkie przedstawione przekształcenia i konstrukcje opisane są wyprowadzonymi przez autora wzorami i zilustrowane rysunkami pokazującymi efekty ich działania, które często są zaskakujące.
Patrycja Lamparska podjęła się opisać matematyczne podstawy różnego rodzaju głosowań i wyborów. Załóżmy, że w wyborach startuje pewna liczba kandydatów i każdy z wyborców ustawia ich w kolejności od najlepszego do najgorszego (dla różnych wyborców ta kolejność może być różna). Kto jest zwycięzcą takiego głosowania? To zależy od przyjętej metody głosowania, czyli sposobu wyznaczania zwycięzcy (lub zwycięzców) w zależności od tego, jak kandydatów uporządkowali wyborcy. Autorka podaje formalny opis tego zagadnienia, wskazuje naturalne warunki, jakie powinny spełniać metody głosowania, i przedstawia kilka takich metod, ilustrując ich działanie przykładami. Wkładem własnym autorki jest opracowanie i przedstawienie trzech nowych metod głosowania.
Autor jest przewodniczącym Jury Konkursu
Finałowe prace wraz z większą ilością informacji o konkursie, w tym o nowej 48. edycji, można odnaleźć na stronie delty Konkursy > Konkurs Prac Uczniowskich